训练情况
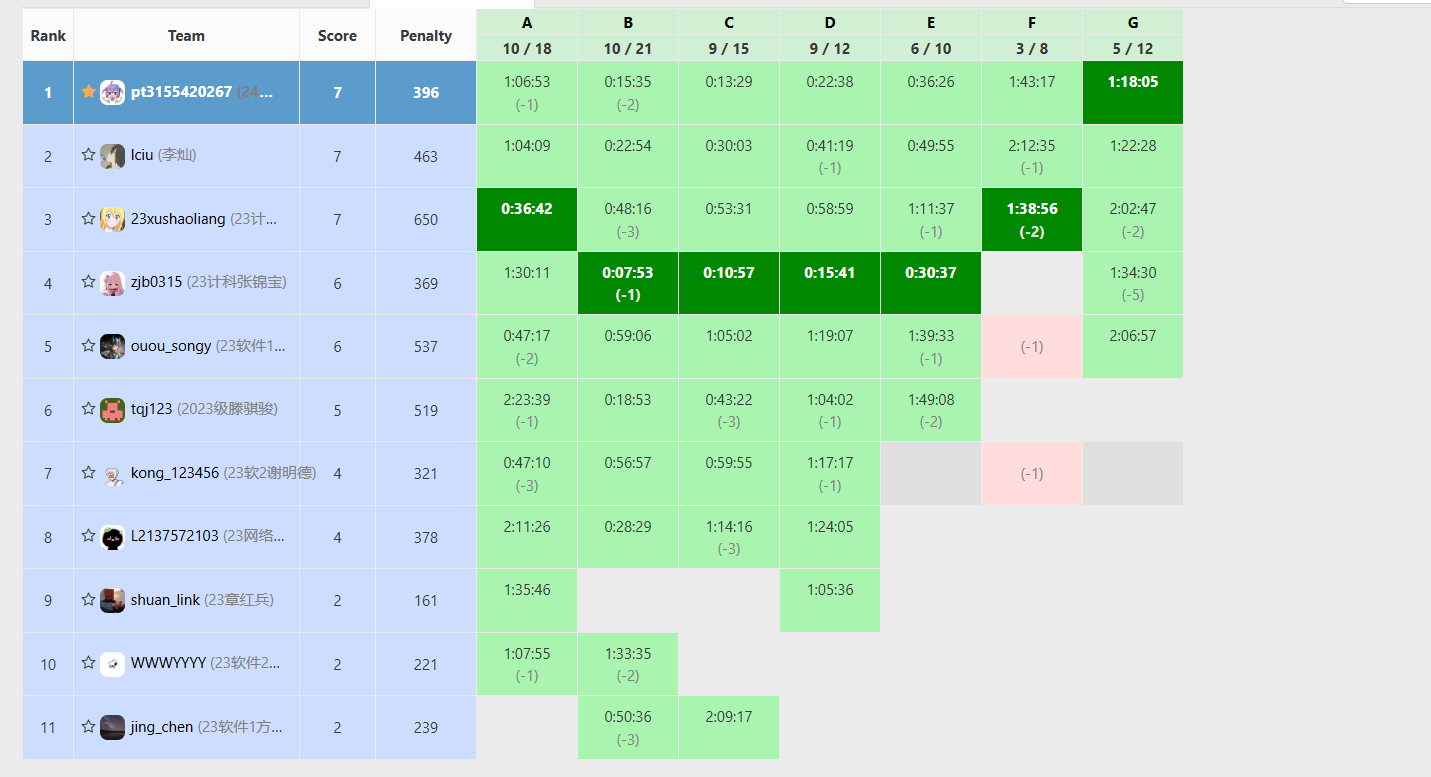
赛后反思
被小数据背刺了,吃了几发RE,不过还是调出来了
A题
我们先考虑将连续的 v 先换成 w,之后就是统计子序列 wow 的个数,我们只需要找每个 o 前面有多少个 w,之后有多少个 w,根据乘法原理可知,这个 o 对答案的贡献就是两个相乘,维护前面和后面的 w 我们可以考虑使用前后缀和。
#include <bits/stdc++.h>
#define int long longusing namespace std;signed main(){string s; cin>>s;int n = s.size();if(n<=2){cout<<0<<endl;return 0;}string t;for(int i = 0;i<n;i++){if(s[i] == 'o') t+="o";if(i==0) continue;if(s[i] == 'v' && s[i-1] == 'v') t+="w";}n = t.size();vector<int> pre(n+1);vector<int> suf(n+1);pre[0] = (t[0] == 'w');suf[n-1] = (t[n-1] == 'w');for(int i = 1;i<n;i++){pre[i] = pre[i-1] + (t[i] == 'w');}for(int i = n-2;~i;i--){suf[i] = suf[i+1] + (t[i] == 'w');}int ans = 0;for(int i = 0;i<n;i++){if(t[i] == 'o') ans += (pre[i]*suf[i]);}cout<<ans<<endl;return 0;
}
B题
找数列中是否有 \(m\) 个大于 \(\frac{sum}{4m}\) 个元素,我们先直接求个和,再判断每一位是否符合要求即可,注意除法会有精度和取整问题,所以我们考虑把除法移到左边去乘。
#include <bits/stdc++.h>using namespace std;int main(){int n,m; cin>>n>>m;vector<int> a(n + 1);int sum = 0;for(int i = 1;i<=n;i++) cin>>a[i],sum+=a[i];int cnt = 0;for(int i = 1;i<=n;i++){if(a[i]*4*m < sum) cnt++;}if(n-cnt>=m) cout<<"Yes"<<endl;else cout<<"No"<<endl;return 0;
}
C题
很显然要绝对值最接近 \(0\),\(n\) 要减去 \(k\) 倍的 \(m\),并且这个 \(k\) 要足够大,这就是直接 \(n \mod m\) 即可,再和负数的绝对值情况取大值即可。
#include <bits/stdc++.h>
#define int long long
using namespace std;signed main(){int n,m; cin>>n>>m;cout<<min(n%m,abs(n%m-m));return 0;
}
D题
简单的 DP,我们设计状态 \(dp_{ij}\) 为走到第 \(i\) 行,\(j\) 列的路线数,它可以从它的上一行和上一列转移过来,求一个和即可,记得跳过全部偶数的情况。
#include <bits/stdc++.h>
#define int long longusing namespace std;int dp[33][33];signed main(){int n,m; cin>>n>>m;dp[1][1] = 1;for(int i = 1;i<=n;i++){for(int j = 1;j<=m;j++){if(i%2==0&&j%2==0) continue;if(i==1&&j==1) continue;dp[i][j] = dp[i-1][j] + dp[i][j-1];}}
// for(int i = 1;i<=n;i++){
// for(int j = 1;j<=m;j++){
// cout<<dp[i][j]<<" ";
// }
// cout<<endl;
// }cout<<dp[n][m]<<endl;return 0;
}
E题
我们判断曲线是否会经过圆,我们只需要判断起点和终点一个在圆内,一个在圆外即可,这样无论曲线怎么画都得经过这个圆,直接统计答案即可。
#include <bits/stdc++.h>using namespace std;double dis(int x,int y,int xx,int yy){return sqrt((x-xx)*(x-xx)+(y-yy)*(y-yy));
}int main(){int n; cin>>n;vector<int> x(n + 1),y(n + 1),r(n + 1);for(int i = 1;i<=n;i++) cin>>x[i];for(int i = 1;i<=n;i++) cin>>y[i];for(int i = 1;i<=n;i++) cin>>r[i];int xa,ya,xb,yb; cin>>xa>>ya>>xb>>yb;int ans = 0;for(int i = 1;i<=n;i++){double res1 = dis(xa,ya,x[i],y[i]);double res2 = dis(xb,yb,x[i],y[i]);if((res1<r[i]&&res2>r[i])||(res1>r[i]&&res2<r[i]))ans++;}cout<<ans<<endl;return 0;
}
F题
我们发现这是一道最长公共子序列题,但是这题没有办法使用 \(O(n^2)\) 的 DP,但是我们发现这一题是一个排列,我们可以考虑记录每个排列出现的位置,既然要最长公共子序列,我们只需要每一个排列的下标递增即可,通过下标位置的递增,这就可以转换成最长上升子序列,使用二分算法 \(O(nlogn)\) 做。
#include<bits/stdc++.h>using namespace std;int main(){int n; cin>>n;vector<int> a(n + 1);vector<int> b(n + 1);vector<int> pos(n + 1);for(int i = 1;i<=n;i++) cin>>a[i],pos[a[i]] = i;for(int i = 0;i<=n;i++) a[i] = INT_MAX;for(int i = 1;i<=n;i++) cin>>b[i];for(int i = 1;i<=n;i++){int p = lower_bound(a.begin() + 1,a.end(),pos[b[i]]) - a.begin();a[p] = pos[b[i]];}int ans = lower_bound(a.begin() + 1,a.end(),a[0]) - a.begin() - 1;cout<<ans<<endl;return 0;
}
G题
我们想要 gcd 最大,我们显然发现一对数的 gcd 是会小于等于它的较小的数,所以我们构造的数列的 gcd 必定等于最小的 a,之后就是统计能这样构造的数组一共有多少个,只要每个数在 \(a_i\) 的范围内,并且都是那个 gcd (最小的 \(a_i\))的倍数即可,计算出每一位有多少种放置方法,最后根据乘法原理全部乘起来就是答案了。
#include <bits/stdc++.h>
#define int long longusing namespace std;
const int modd = 1e9+7;
signed main(){int n; cin>>n;vector<int> a(n + 1);for(int i = 1;i<=n;i++) cin>>a[i];sort(a.begin() + 1,a.end());int cnt = 1;for(int i=1;i<=n;i++){cnt = cnt % modd * (a[i]/a[1])%modd;}cout<<a[1]<<" "<<cnt%modd<<endl;return 0;
}