2024数模b题-问题一思路构建
样本量计算
根据置信空间的计算公式,
逆累积分布函数(ICDF):
- 逆累积分布函数(ICDF)是从累积分布函数的值反推出对应的Z分数。
- 在MATLAB中,norminv 函数就是计算标准正态分布的逆累积分布函数的值
我们通过这个公式来得到
我们可以得到
对于95%置信水平,我们能得到Z=1.96
对于90%置信水平,我们能得到Z=1.645
接下来我们可以根据两种情况来判断,
第一种:
在95%置信水平下,当p1>p0=10%时,拒收这批零配件, 当样本检测到的次品率显著高于 标称值时拒收
第二种:
在90%置信水平下,当p2<p0=10%时,接收这批零配件,当次品率在一个合理的范围内,接收这批零配件。
因此我们可以计算样本量的值,
利用两个临界值的Z,求得95%和90%置信程度下的 最小样本量
但是还是有一个问题那就是,我们让样本足够小,但是接受率我们没有进行限定,因此我们还要讨论接受率p和样本量n的关系
p值在统计假设检验中起着核心作用。它提供了关于样本数据与假设之间一致性的度量。具体来说,p 帮助我们判断在给定的零假设(H0)下,观察到的数据(或更极端的数据)发生的概率有多大。
然后我们去找到关于p 和 n 的关系图然后得到
问题二
思路
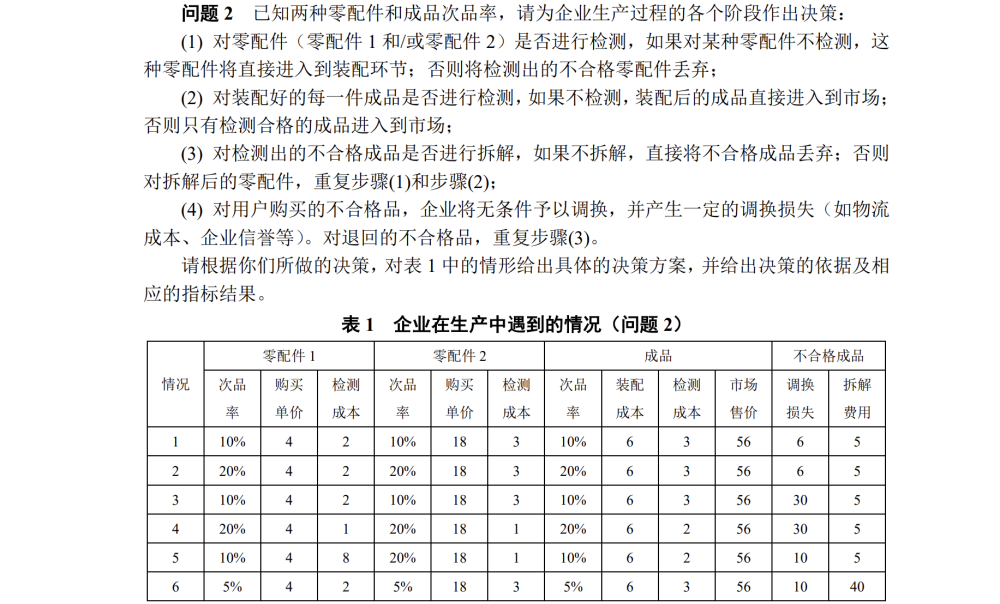
企业要在生产过程中做出决策,然后找到最小的总成本数,然后根据零配件,成品,不合格成品的选择进行动态规划,找到最优解进行优化。
模型设计
此题的关键就是考虑状态转移方程,动态规划的思路
为了使模型更加清晰,我们可以将问题划为三个阶段
第一阶段:零配件采购和检测
第二阶段:成本的装配和检测
第三阶段:不合格成品的调换和拆解
我们来利用这三个阶段进行动态规划模型的建立
动态规划模型分析
- 问题定义给定一系列的成本和概率参数,我们需要决定在每个阶段应该采取的最佳行动,从而最大化总收益或最小化总成本。
定义自变量
n:批量大小(生产的产品数量)。
p_1:零配件1的次品率。
p_2:零配件2的次品率。
fp:成品的次品率。
cg1:零配件1的采购单价。
cg2:零配件2的采购单价。
jc1:零配件1的检测成本。
jc2:零配件2的检测成本。
zp:成品的装配成本。
cjc:成品的检测成本。
dh:成品的调换损失。
cj:不合格成品的拆解费用。
s:成品的市场售价。
2.状态表示
第一阶段:零配件采购和检测
状态表示 (a1,a2)
a1表示是否检测零配件1,a2表示是否检测零配件2 (1表示检测,0表示不检测)
第二阶段:成本的装配和检测
状态表示 a3
a3表示是否检测成品(1表示检测,0表示不检测)
第三阶段:不合格成品的调换和拆解
状态表示 a4
a4表示是否拆解不合格产品(1表示拆解,0表示不拆解)
3.转移方程
第三阶段:不合格成品的调换和拆解
这种分两种情况
第一n种:拆解不合格成品
那么得到a4=1
则状态转移方程可得到
Y(3,1)=−cj⋅n1−(zp+cjc)⋅n1
第二种:不拆解不合格成品
由于 a4=0
则得到
Y(3,0)=0
第二阶段:成本的装配和检测
这个也是分两种情况
第一种:不检测成品
那么得到a3=0
不检测成品状态转移方程为
Y(2,0)=−fp⋅dh⋅𝑛1+(1−fp)⋅s⋅𝑛1+Y(3,a4)
第二种:检测成品
那么得到a4=0
检测成品的状态转移方程
Y(2,1)=−cjc⋅n1+(1−fp)⋅s⋅n1+Y(3,a4)
第一阶段:零配件采购和检测
分四种情况
第一种:检测零件一检测零件二
那么a1=1,a2=1
那么状态转移方程
𝑌(1,1,1)=−(jc1+cg1+jc2+cg2)⋅𝑛1+𝑌(2,a3)Y(1,1,1)=−(jc1+cg1+jc2+cg2)⋅n1+Y(2,a3)
第二种:检测零件一,不检测零件二
那么a1=1,a2=0
状态转移方程
Y(1,1,0)=−(cg1+jc2+cg2+(p_1+p_2)⋅n1)+Y(2,a3)
第三种:不检测零件一,检测零件二
那么a1=0,a2=1
状态转移方程
𝑌(1,0,1)=−(cg1+cg2+jc2+(p_1+p_2)⋅𝑛)+𝑌(2,a3)Y(1,0,1)=−(cg1+cg2+jc2+(p_1+p_2)⋅n)+Y(2,a3)
第四种:不检测零件一,不检测零件二
那么a1=0,a2=0
状态转移方程
Y(1,0,0)=−(cg1+cg2+(p_1+p_2)⋅n1)+Y(2,a3)
步骤
计算阶段三-->阶段二-->阶段一-->最优解
代码如下
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用黑体显示中文
p_1 = [0.1,0.2,0.1,0.2,0.1,0.05] # 零配件1的次品率
p_2 = [0.1,0.2,0.1,0.2,0.2,0.05] # 零配件2的次品率
fp = [0.1,0.2,0.1,0.2,0.1,0.05] # 成品的次品率
cg1 = [4,4,4,4,4,4] # 零配件1的采购单价
cg2 = [18,18,18,18,18,18] # 零配件2的采购单价
jc1 = [2,2,2,1,8,2] # 零配件1的检测成本
jc2 = [3,3,3,1,1,3] # 零配件2的检测成本
zp = [6,6,6,6,6,6] # 成品的装配成本
cjc =[3,3,3,2,2,3] # 成品的检测成本
dh= [6,6,30,30,10,10] # 成品的调换损失
cj = [5,5,5,5,5,40] # 不合格成品的拆解费用
colors = ['r', 'g', 'b', 'c', 'm', 'y']
s = 56 # 成品的市场售价
# 初始化DP表和决策路径表
dp = {}
decision_path = {}
dic={}
# 阶段3:不合格成品拆解与市场流转决策
def calculate_jd_3(n,p_1,p_2,fp,cg1,cg2,jc1,jc2,zp,cjc,dh,cj,s):
# 不拆解不合格成品
dp[(3, 0)] = -fp * (zp+ cjc+ cg1 + cg2) * n
decision_path[(3, 0)] = "不拆解不合格成品"
# 拆解不合格成品
dp[(3, 1)] = -cj * n # 注意这里需要减去拆解费用,后续计算阶段1的收益
decision_path[(3, 1)] = "拆解不合格成品"
# 阶段2:成品装配和检测决策
def calculate_jd_2(n,p_1,p_2,fp,cg1,cg2,jc1,jc2,zp,cjc,dh,cj,s):
# 不检测成品
dp[(2, 0)] = -fp * dh* n + (1 - fp) * s * n + dp[(3, 0)]
decision_path[(2, 0)] = "不检测成品"
# 检测成品
dp[(2, 1)] = -cjc * n + (1 - fp) * s * n + dp[(3, 1)]
decision_path[(2, 1)] = "检测成品"
# 阶段1:零配件采购和检测决策
def calculate_jd_1(n,p_1,p_2,fp,cg1,cg2,jc1,jc2,zp,cjc,dh,cj,s):
# 检测零配件1和零配件2
dp[(1, 1, 1)] = -(jc1 * n + cg1 * n + jc2 * n + cg2 * n) + dp[(2, 1)]
decision_path[(1, 1, 1)] = "检测零配件1和零配件2"
# 检测零配件1,不检测零配件2
dp[(1, 1, 0)] = -(jc1 * n + cg1 * n + cg2 * n + p_2 *dh* n) + dp[(2, 1)]
decision_path[(1, 1, 0)] = "检测零配件1,不检测零配件2"
# 不检测零配件1,检测零配件2
dp[(1, 0, 1)] = -(cg1 * n + jc2 * n + cg2 * n + p_1 * dh * n) + dp[(2, 1)]
decision_path[(1, 0, 1)] = "不检测零配件1,检测零配件2"
# 不检测零配件1和零配件2
dp[(1, 0, 0)] = -(cg1 * n + cg2 * n + p_1 * dh * n + p_2 * dh * n) + dp[(2, 1)]
decision_path[(1, 0, 0)] = "不检测零配件1和零配件2"
def calculate_n_money(n,p_1,p_2,fp,cg1,cg2,jc1,jc2,zp,cjc,dh,cj,s,j):
calculate_jd_3(n,p_1,p_2,fp,cg1,cg2,jc1,jc2,zp,cjc,dh,cj,s); # 计算阶段3
calculate_jd_2(n,p_1,p_2,fp,cg1,cg2,jc1,jc2,zp,cjc,dh,cj,s); # 计算阶段2
calculate_jd_1(n,p_1,p_2,fp,cg1,cg2,jc1,jc2,zp,cjc,dh,cj,s); # 计算阶段1
# 找到最优的决策和路径
optimal_value = max(dp.values()) # 最优总收益
optimal_state = max(dp, key=dp.get) # 最优状态
# 输出最优结果和对应的决策路径
print("最优总收益和成本:", optimal_value)
print("最优策略路径:")
# 回溯决策路径
# if len(optimal_state) == 3:
# 从阶段1开
calculate_1_state = max(dp.keys(), key=lambda k: dp[k] if k[0] == 1 else float('-inf'))
print(f"阶段1:{decision_path[calculate_1_state]}")
calculate_2_state = max(dp.keys(), key=lambda k: dp[k] if k[0] == 2 else float('-inf'))
print(f"阶段2:{decision_path[calculate_2_state]}")
calculate_3_state = max(dp.keys(), key=lambda k: dp[k] if k[0] == 0 else float('-inf'))
print(f"阶段3:{decision_path[calculate_3_state]}")
dic[i]=optimal_value#将这种情况对应的最优策略的最大利润
for j in range(0,6,1):
# 初始化DP表和决策路径表
dp = {}
decision_path = {}
dic={}
for i in range(1,100,1):
calculate_n_money(i,p_1[j],p_2[j],fp[j],cg1[j],cg2[j],jc1[j],jc2[j],zp[j],cjc[j],dh[j],cj[j],s,j)
keys=dic.keys()
values=dic.values()
plt.bar(keys, values,color=colors[j])
plt.xlabel('情况'+str(j+1))
plt.ylabel('利润')
plt.title('情况'+str(j+1)+"与样本量的关系图")
plt.show()
# plt.figure() # 创建一个新的图形窗口