在最近的工作中,遇到一个浮点数格式化问题,蛮有意思的,是之前所没遇到过的知识点,在此整理总结。
问题描述
一句话描述问题,将一个3位小数的浮点数,格式化为2位小数的,是什么样的舍入规则?一般想着的是四舍五入,但实际不是,具体如何,看如下程序。
测试代码如下:
void test_float_format()
{const int nBufSize = 32;char szBuf[nBufSize] = { 0 };float d1 = 10.564; // 10.505 10.515 10.525float d2 = 10.565;float d3 = 10.566; // sprintf_s(szBuf, nBufSize, "%.2f", d1);printf("d1: %s\n", szBuf);memset(szBuf, 0, nBufSize);sprintf_s(szBuf, nBufSize, "%.2f", d2);printf("d2: %s\n", szBuf);memset(szBuf, 0, nBufSize);sprintf_s(szBuf, nBufSize, "%.2f", d3);printf("d3: %s\n", szBuf);memset(szBuf, 0, nBufSize);
}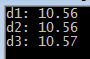
上面的第二个输出比较怪异,按照数学上4舍5入规则,应该输出10.57的,实际上却是10.56,经过其他验证,发现以4结尾的,格式化时都舍入,6结尾的都进位。当为5结尾时,测试结果如下图所示:

上述测试程序在Windows和Linux环境上的结果都是如此。
出现上面这种情况,是我不理解的,当结尾小数为5时,不同类型的舍入情况还不一样,这是为什么呢?
在编码上,有以下几点要注意:
-
一个小数值,默认为
double类型,除非结尾增加f后缀,改为float类型,否则编译器会提示如下错误:
-
double类型占用8个字节,有15位有效数字;float类型占用4个字节,有7位有效数字。还有一种long double类型,通常占据12个字节,精度不低于double类型,这种用的较少。 -
在涉及到浮点数计算时,优先使用
double类型。
浮点数存储原理
由于浮点数使用固定字节,能表示的数值精度有限,将无穷多个浮点数映射到有效浮点范围时,会引入舍入误差。
具体来说,就是当某个浮点数的准确数值,二进制化后,落在某两个二进制浮点数数值范围之间时,如何处理就是个问题。
对此,IEEE 754 arithmetic and rounding规定了4种舍入规则:
1. Round to nearest: 四舍五入到Frac最接近的偶数位> The system chooses the nearer of the two possible outputs. If the correct answer is exactly halfway between
> the two, the system chooses the output where the least significant bit of Frac is zero. This behavior
> (round-to-even) prevents various undesirable effects.> This is the default mode when an application starts up. It is the only mode supported by the ordinary
> floating-point libraries. Hardware floating-point environments and the enhanced floating-point libraries
> support all four rounding modes.从两个可能的输出中选择较近的output。如果正确答案正好介于两者之间,则选择 Frac 的最低有效位为零的输出。
2. Round up 向正无穷大舍入选择两个可能的输出中较大的一个,称为 round toward +
3. Round down 向负无穷大舍入选择两个可能的输出中较小的一个
4. Round toward zero 朝零舍入,称为 round toward -选择两个可能的输出中,更接近0的那一个,称为 round toward 0
C语言的浮点库默认为采用模式1,可通过 fesetround 函数来设置舍入模式。
针对模式1的理解,在进行舍入处理时,系统会选择与真实值最靠近的浮点数来表示。比如将3位小数(eg:10.564)格式化为2位,它会在10.57和10.56中进行判断,10.564与10.57相差0.006,与10.56相差0.004,取相差值较小的为准,因此取 10.56。
这种方法对小数位小于等于4或大于等于6的情况是OK的,现在考虑小数尾位为5的情况。
将10.565格式化为2位小数,有10.56和10.57两种选择,两者距离一样,按照上述规范要求,此时应选择Frac最低位为0的那个数。
10.56的二进制表达如下:
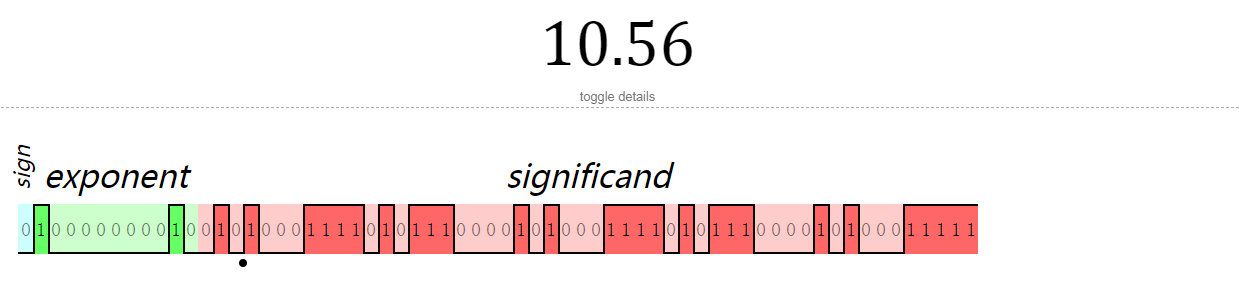
10.57的二进制表达如下:
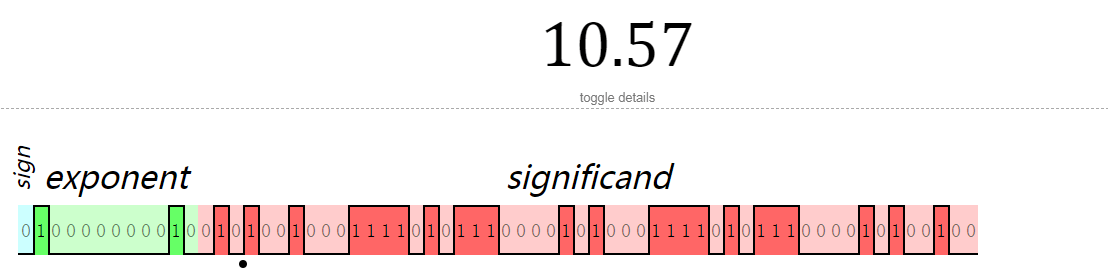
一个浮点数在IEEE 754标准中,由三部分组成:
- sign 位于最高位的符号位,表示正负号,0正1负,占 1bit。
- exponent 位于中间的指数位,表示大小范围, float占8位,double占11位。
- fraction 位于最低位的有效数,表示精度范围,float占23位,double占52位。
因10.57的最低位有效数值为0,因此,在舍入保持2位小数时,取10.57。反复看了规范说明,规范里面针对的好像是1位小数,舍入为整数的场景。针对多位小数的情况,没有说明,搞不清楚为什么和实际输出的不一样。
工程规避
如果想要在工程中规避这种不确定的舍入,可以手动增加偏移值,使得格式化结果4舍5入的数学认知。比如你要将3位小数格式化为2位,可以加上 0.0005 偏移。
扩大下,如果要对N位小数的原始数据进行格式化,使其满足4舍5入,可加上N+1位的,结尾为5的小数,这样可满足4舍5入规则。
同样的3位浮点数,保留2位有效数字,不同数值范围、不同存储格式的舍入表现不一样,很令人疑惑。
如有知道详情的,请不吝赐教。
参考链接:
- https://trekhleb.dev/blog/2021/binary-floating-point/
- https://bartaz.github.io/ieee754-visualization/
- 将十进制转换为任意形式
- IEEE 574学习计算器