运筹学两阶段法中的人工变量数量问题
在运筹学的两阶段法中,为了找到线性规划(LP)问题初始解的可行性,通常需要在约束条件中引入人工变量。以下是我学习课本后对相关内容的总结。
1. 人工变量的引入条件
-
等式约束(=):每一个等式约束需要引入一个人工变量。
-
大于等于约束(≥):每一个“大于等于”约束需要引入一个松弛变量和一个人工变量。
-
小于等于约束(≤):通常通过引入松弛变量即可转化为等式约束,不需要人工变量
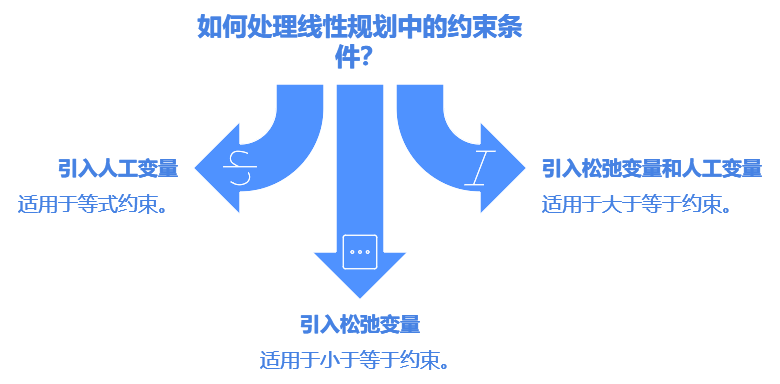
因此,需要的人工变量数量通常等于等式约束和大于等于约束的个数之和。
2. 单位向量的作用
如果约束条件中已经包含了一些单位向量,可以减少所需的人工变量数量,因为这些单位向量可以直接作为初始基变量,从而保证了初始解的可行性。具体来说:
- 设总共需要引入人工变量的约束个数为
m,但如果其中已有a个单位向量,那么只需为剩下的m - a个约束引入人工变量即可。
3. 公式总结
最终,需要引入的人工变量个数可以表示为:
需要的人工变量个数 = m - a
其中:
m是等式约束和大于等于约束的总个数。a是约束条件中已包含的单位向量数量。
4. 示例
假设一个问题中有 3 个等式约束和 1 个大于等于约束,通常情况下需要引入 4 个人工变量(即 m = 4)。如果这些约束中已经包含 2 个单位向量(即 a = 2),那么实际只需引入 4 - 2 = 2 个人工变量。





![[Zer0pts2020]easy strcmp](https://img2023.cnblogs.com/blog/3546358/202411/3546358-20241105183601446-2140152418.png)