【考试题解】多校A层冲刺NOIP2024模拟赛18

news/2024/11/5 20:44:13/文章来源:https://www.cnblogs.com/ywhhdjser-97/p/18528763

目录
  • A. 选彩笔(rgb)
    • 题目内容
    • 部分分
    • 正解
      • 思路
      • 代码
  • B. 兵蚁排序(sort)
    • 题目内容
    • 部分分
      • 75pts
    • 正解
      • 思路
      • 代码
  • C. 人口局DBA(dba)
    • 题目内容
    • 部分分
      • 60pts
    • 正解
      • 思路
      • 代码
  • D. 银行的源起(banking)

A. 选彩笔(rgb)

题目内容

有 \(N\) 支彩笔，每支彩笔有 \(R_i,G_i,B_i\) 三个属性。定义两只彩笔 \(i,j\) 的 Difference 值为 \(max(|R_i-R_j,G_i-G_j,B_i-B_j|)\)。定义一套彩笔的 Colorfulness 值为选中彩笔中 Difference 的最大值。求取出 \(K\) 支笔组成一套的 Colorfulness 的最小值。\(R_i,G_i,B_i\in[0,255]\)，\(K,N\in[2,10^5]\)

部分分

我不到啊。

正解

思路

观察到题面里鲜明的“最大值最小”，于是考虑二分答案。把每支笔都抽象为三维空间中的点，于是题目变为找一个正方体，包含至少 \(K\) 个点，求正方体最短边长。首先，有一个点在正方体其中一个顶点上的方案肯定不劣。于是check里枚举每一个点，分别把它作为正方体的八个顶点试一试。然后找一个正方体里有多少个点就是经典问题了。由于我们是实时询问，所以 \(O(n\log^2n)\) 的三维偏序不是很行得通。注意到至于很小，所以直接三维前缀和秒掉。复杂度 \(O(w^3+n\log w)\)。注意：如果只钦定它为三个值都取到 \(max\) 的顶点，可以过掉所有的大小样例，但是会挂在下面的数据：

输入：

2 2
1 2 2
2 1 1

输出：

1

锅了的会输出2。

代码

#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define inf 0x3f3f3f3f
int a,b,u[100001],v[100001],w[100001],col[262][262][262],pre[262][262][262];
il bool check(int x)
{for(ri i=1;i<=a;i++){ri x1=max(1,u[i]-x),y1=max(1,v[i]-x),z1=max(1,w[i]-x);ri x2=u[i],y2=v[i],z2=w[i];ri rn=pre[x2][y2][z2];rn-=pre[x1-1][y2][z2]+pre[x2][y1-1][z2]+pre[x2][y2][z1-1];rn+=pre[x1-1][y1-1][z2]+pre[x1-1][y2][z1-1]+pre[x2][y1-1][z1-1];rn-=pre[x1-1][y1-1][z1-1];if(rn>=b){return true;}z1=w[i],z2=min(256,w[i]+x);rn=pre[x2][y2][z2];rn-=pre[x1-1][y2][z2]+pre[x2][y1-1][z2]+pre[x2][y2][z1-1];rn+=pre[x1-1][y1-1][z2]+pre[x1-1][y2][z1-1]+pre[x2][y1-1][z1-1];rn-=pre[x1-1][y1-1][z1-1];if(rn>=b){return true;}z1=max(1,w[i]-x),z2=w[i];y1=v[i],y2=min(256,v[i]+x);rn=pre[x2][y2][z2];rn-=pre[x1-1][y2][z2]+pre[x2][y1-1][z2]+pre[x2][y2][z1-1];rn+=pre[x1-1][y1-1][z2]+pre[x1-1][y2][z1-1]+pre[x2][y1-1][z1-1];rn-=pre[x1-1][y1-1][z1-1];if(rn>=b){return true;}z1=w[i],z2=min(256,w[i]+x);rn=pre[x2][y2][z2];rn-=pre[x1-1][y2][z2]+pre[x2][y1-1][z2]+pre[x2][y2][z1-1];rn+=pre[x1-1][y1-1][z2]+pre[x1-1][y2][z1-1]+pre[x2][y1-1][z1-1];rn-=pre[x1-1][y1-1][z1-1];if(rn>=b){return true;}z1=max(1,w[i]-x),z2=w[i];y1=max(1,v[i]-x),y2=v[i];x1=u[i],x2=min(256,u[i]+x);rn=pre[x2][y2][z2];rn-=pre[x1-1][y2][z2]+pre[x2][y1-1][z2]+pre[x2][y2][z1-1];rn+=pre[x1-1][y1-1][z2]+pre[x1-1][y2][z1-1]+pre[x2][y1-1][z1-1];rn-=pre[x1-1][y1-1][z1-1];if(rn>=b){return true;}z1=w[i],z2=min(256,w[i]+x);rn=pre[x2][y2][z2];rn-=pre[x1-1][y2][z2]+pre[x2][y1-1][z2]+pre[x2][y2][z1-1];rn+=pre[x1-1][y1-1][z2]+pre[x1-1][y2][z1-1]+pre[x2][y1-1][z1-1];rn-=pre[x1-1][y1-1][z1-1];if(rn>=b){return true;}z1=max(1,w[i]-x),z2=w[i];y1=v[i],y2=min(256,v[i]+x);rn=pre[x2][y2][z2];rn-=pre[x1-1][y2][z2]+pre[x2][y1-1][z2]+pre[x2][y2][z1-1];rn+=pre[x1-1][y1-1][z2]+pre[x1-1][y2][z1-1]+pre[x2][y1-1][z1-1];rn-=pre[x1-1][y1-1][z1-1];if(rn>=b){return true;}z1=w[i],z2=min(256,w[i]+x);rn=pre[x2][y2][z2];rn-=pre[x1-1][y2][z2]+pre[x2][y1-1][z2]+pre[x2][y2][z1-1];rn+=pre[x1-1][y1-1][z2]+pre[x1-1][y2][z1-1]+pre[x2][y1-1][z1-1];rn-=pre[x1-1][y1-1][z1-1];if(rn>=b){return true;}}return false;
}
int main()
{freopen("rgb.in","r",stdin);freopen("rgb.out","w",stdout);scanf("%d%d",&a,&b);for(ri i=1;i<=a;i++){scanf("%d%d%d",&u[i],&v[i],&w[i]);u[i]++;v[i]++;w[i]++;col[u[i]][v[i]][w[i]]++;}for(ri i=1;i<=256;i++){for(ri j=1;j<=256;j++){for(ri k=1;k<=256;k++){ri rn=col[i][j][k];rn+=pre[i-1][j][k]+pre[i][j-1][k]+pre[i][j][k-1];rn-=pre[i-1][j-1][k]+pre[i-1][j][k-1]+pre[i][j-1][k-1];rn+=pre[i-1][j-1][k-1];pre[i][j][k]=rn;}}}ri m=0,n=255;while(n!=m){ri l=(m+n)>>1;if(check(l)){n=l;}else{m=l+1;}}printf("%d",m);return 0;
}

B. 兵蚁排序(sort)

题目内容

给你两个序列 \(A,B\)，保证 \(A,B\) 中任意数出现的次数相同。构造方案把 \(A\) 转化为 \(B\)，无解输出-1。多测，\(T\) 组测试数据，\(T\le10,\sum n\le1000,A_i,B_i\in[1,n]\)。

部分分

75pts

暴搜，枚举每次的交换位置，使用哈希来进行去重+剪枝，然后跑的飞快。

点击查看代码 
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define inf 0x3f3f3f3f
int a,b,c[1001],d[1001],ans;
const int base=11491;
vector<int>vec;
deque<pair<int,int>>que;
map<pair<unsigned long long,int>,int>mp;
unsigned long long mdd;
il unsigned long long _hash(const vector<int> &x)
{register unsigned long long rn=0;for(ri i:x){rn=rn*base+i;}return rn;
}
bool dfs(int x)
{if(x>ans){return false;}register unsigned long long re=_hash(vec);if(re==mdd){puts("0");printf("%d\n",x-1);while(!que.empty()){printf("%d %d\n",que.front().first,que.front().second);que.pop_front();}return true;}if(mp[{re,a}]&&mp[{re,a}]<=x){return false;}mp[{re,a}]=x;vector<int>now(vec);for(ri i=0;i<vec.size()-1;i++){for(ri j=i+1;j<vec.size();j++){sort(vec.begin()+i,vec.begin()+j+1);que.push_back({i+1,j+1});if(dfs(x+1)){return true;}que.pop_back();vec=now;}}return false;
}
int main()
{freopen("sort.in","r",stdin);freopen("sort.out","w",stdout);scanf("%d",&a);while(a--){scanf("%d",&b);vec.clear();for(ri i=1;i<=b;i++){scanf("%d",&c[i]);vec.push_back(c[i]);}mdd=0;for(ri i=1;i<=b;i++){scanf("%d",&d[i]);mdd=mdd*base+d[i];}ans=b*b;if(!dfs(1)){puts("-1");}}return 0;
}

正解

思路

由于题目保证 \(A,B\) 中任意数出现的次数相同，所以我们对于 \(A\) 中任意数，可以找到其对应 \(B\) 中的位置。然后根据这个东西进行冒泡排序，使映射位置靠前的往前走，如果这么走不合法，那么就是无解。具体地，如果存在位置 \(i\) 使得它后面有数权值比它大，而映射位置比它小，那么无解；否则必能通过我们的冒泡排序找到可行解。由于是冒泡排序，所以复杂度 \(O(n^2)\)。

代码

#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define inf 0x3f3f3f3f
int a,b,c[1001],d[1001],ans,to[1001];
queue<int>que[1001];
queue<pair<int,int>>ask;
il bool bubble()
{for(ri i=1;i<b;i++){for(ri j=1;j<b;j++){if(to[j]>to[j+1]){if(c[j]<c[j+1]){while(!ask.empty()){ask.pop();}return false;}else{swap(c[j],c[j+1]);swap(to[j],to[j+1]);ask.push({j,j+1});}}}}return true;
}
int main()
{freopen("sort.in","r",stdin);freopen("sort.out","w",stdout);scanf("%d",&a);while(a--){scanf("%d",&b);for(ri i=1;i<=b;i++){scanf("%d",&c[i]);que[c[i]].push(i);}for(ri i=1;i<=b;i++){scanf("%d",&d[i]);to[que[d[i]].front()]=i;que[d[i]].pop();}ans=bubble();if(ans){puts("0");printf("%d\n",ask.size());while(!ask.empty()){printf("%d %d\n",ask.front().first,ask.front().second);ask.pop();}}else{puts("-1");}}return 0;
}

C. 人口局DBA(dba)

题目内容

给你一个 \(m\) 进制数 \(n\)，长度为 \(L\) 且首位保证不为 \(0\)，求所有 \(\lt n\) 的 满足 \(S(x)=S(n)\) 的 \(m\) 进制数 \(x\) 的个数，答案对 \(10^9+7\) 取模。\(S(n)\) 为 \(n\) 在 \(m\) 进制下各位数字之和。\(m,L\in[1,2000]\)。

部分分

60pts

数位DP，但是赛时打锅了。

正解

思路

推式子。设 \(H(l,s)\) 表示长度为 \(l\) 总和为 \(s\) 的方案数。这里最困难的地方在于要保证任意数位的数要 \(\lt m\)。于是考虑容斥，发现这玩意儿推二项式反演好像很有前途，于是在 \(l,s\) 固定的情况下，设 \(F(x)\) 表示恰好有 \(i\) 个位置不满足 \(\lt m\) 条件的方案数，\(G(x)\) 表示至少有 \(i\) 个位置不满足 \(\lt m\) 条件的方案数，列出二项式反演的式子：

\[G(x)=\sum\limits_{i=x}^{l}\binom{i}{x}F(i) \]

\[F(x)=\sum\limits_{i=x}^{l}(-1)^{i-x}\binom{i}{x}G(i) \]

我们先看 \(G(x)\) 的求解。先忽略限制，插板法可得方案数为 \(\binom{s+l-1}{l-1}\)。这里可以这么理解：原来有 \(m\) 个球，现在加进去 \(n-1\) 个球，然后再随便选 \(n-1\) 个球染色，将原序列分为 \(n\) 部分。选上 \(x\) 个位置 \(\ge m\)，就先让这 \(x\) 个位置值为 \(m\)，然后剩下的数，总和为 \(s-xm\) 随便分给所有位置。方案数就是 \(\binom{s-xm+l-1}{l-1}\)。注意二项式反演的一式，我们这里 \(G(x)\) 并不是钦定的方案数，而是考虑了被选中位置的方案数。所以 \(G(x)=\binom{l}{x}\binom{s-xm+l-1}{l-1}\)。

然后反演求 \(F(x)\)。

\[\begin{aligned}F(x)&=\sum\limits_{i=x}^{l}(-1)^{i-x}\binom{i}{x}G(i)\\&=\sum\limits_{i=x}^{l}(-1)^{i-x}\binom{i}{x}\binom{l}{i}\binom{s-im+l-1}{l-1}\end{aligned} \]

\(H(l,s)\) 即为对应 \(l,s\) 下的 \(F(0)\) 值。

\[\begin{aligned}H(l,s)=F(0)&=\sum\limits_{i=0}^{l}(-1)^{i}\binom{i}{0}\binom{l}{i}\binom{s-im+l-1}{l-1}\\&=\sum\limits_{i=0}^{l}(-1)^{i}\binom{l}{i}\binom{s-im+l-1}{l-1}\end{aligned} \]

类比数位DP，设第 \(i\) 位所贡献的答案为 \(ans_i\)，则 \(ans_i=\sum\limits_{i=0}^{c[i]-1}H(l-1,s-i)\)，然后推式子：

\[\begin{aligned}ans_k&=\sum\limits_{i=0}^{c[k]-1}H(l-1,s-i)\\&=\sum\limits_{i=0}^{c[k]-1}\sum\limits_{j=0}^{l-1}(-1)^{j}\binom{l-1}{j}\binom{s-i-jm+l-2}{l-2}\\&=\sum\limits_{j=0}^{l-1}(-1)^{j}\binom{l-1}{j}\sum\limits_{i=0}^{c[k]-1}\binom{s-i-jm+l-2}{l-2}\end{aligned} \]

现在重点在于简化后面的那个 \(\sum\) 项。于是充分发扬人类智慧，把这个玩意儿放杨辉三角上，发现这个东西是类似 \(C(a+b-i,b)\) 的东西，也就是杨辉三角上同一列里连续的一段区间。

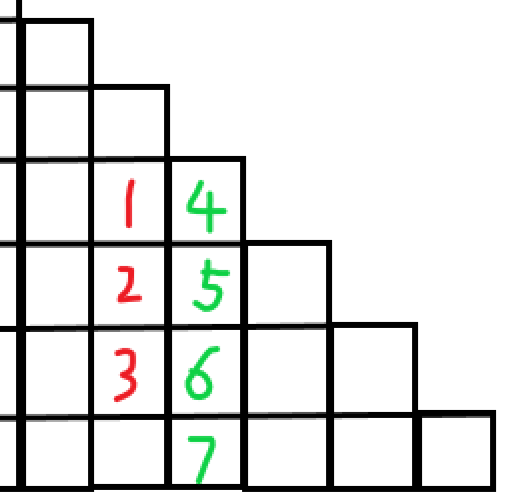
image

我们要求的是红色的 \(1~3\)，现在加进来一个 \(4\)，\(1+4->5,2+5->6,3+6->7\)，于是 \(7-4\) 就是我们想要求得答案。然后写成式子：

\[ans_k=\sum\limits_{j=0}^{l-1}(-1)^{j}\binom{l-1}{j}\binom{s-jm+l-1}{l-1}-\binom{s-c[k]-jm+l-1}{l-1} \]

然后直接求就可以了。注意特判组合数为 \(0\) 的情况。

代码

#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define inf 0x3f3f3f3f
int a,b,c[2002];
const int mod=1e9+7;
long long jc[4000004],ny[4000004],sm,ans;
il long long qpow(long long x,long long y)
{register long long rn=1;while(y){if(y&1){rn=(rn*x)%mod;}x=(x*x)%mod;y>>=1;}return rn;
}
il long long C(int x,int y)
{if(x<y){return 0;}return (((jc[x]*ny[x-y])%mod)*ny[y])%mod;
}
int main()
{freopen("dba.in","r",stdin);freopen("dba.out","w",stdout);scanf("%d%d",&a,&b);for(ri i=b;i>=1;i--){scanf("%d",&c[i]);sm+=c[i];}jc[0]=ny[0]=1;for(ri i=1;i<=a*b;i++){jc[i]=(jc[i-1]*i)%mod;ny[i]=qpow(jc[i],mod-2);}for(ri i=b;i>=1;i--){register long long rn=0;for(ri j=0;j<i;j++){ri op=(j&1)?-1:1;register long long k=(C(i-1,j)*((C(sm-a*j+i-1,i-1)-C(sm-c[i]-a*j+i-1,i-1)+mod)%mod))%mod;rn=(rn+op*k)%mod;rn=(rn+mod)%mod;}ans=(ans+rn)%mod;sm-=c[i];}printf("%lld",ans);return 0;
}

D. 银行的源起(banking)

不会。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/827302.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

学习笔记（二十五）：ArkUi-栅格布局 (GridRow/GridCol)

学习笔记（二十五）：ArkUi-栅格布局 (GridRow/GridCol)

概述： 栅格布局是一种通用的辅助定位工具，对移动设备的界面设计有较好的借鉴作用。主要优势包括：提供可循的规律：栅格布局可以为布局提供规律性的结构，解决多尺寸多设备的动态布局问题。通过将页面划分为等宽的列数和行数，可以方便地对页面元素进行定位和排版。统一的定位…
阅读更多...
WPF TextBlock控件 显示两段文字

WPF TextBlock控件 显示两段文字

WPF TextBlock控件 显示两段文字 TextBlock控件不止显示两段文字，可显示多行。<StackPanel><!-- 显示多行，LineBreak表示换行 --><TextBlock>盼望着，<LineBreak />盼望着，<LineBreak />东风来了，春天的脚步近了。</TextBlock><!-…
阅读更多...
运筹学两阶段法中的人工变量数量问题

运筹学两阶段法中的人工变量数量问题

运筹学两阶段法中的人工变量数量问题 在运筹学的两阶段法中，为了找到线性规划（LP）问题初始解的可行性，通常需要在约束条件中引入人工变量。以下是我学习课本后对相关内容的总结。1. 人工变量的引入条件等式约束（=）：每一个等式约束需要引入一个人工变量。大于等于约束（≥…
阅读更多...
第三十四讲：join语句怎么优化？

第三十四讲：join语句怎么优化？

第三十四讲：join语句怎么优化？ 简概：万年不变的开头 ​ 在上一篇文章中，我和你介绍了 join 语句的两种算法，分别是 Index Nested-Loop Join(NLJ) 和 Block Nested-Loop Join(BNL)。我们发现在使用 NLJ 算法的时候，其实效果还是不错的，比通过应用层拆分成多个语句然后再拼…
阅读更多...
Cursor使用

Cursor使用

Cursor是一款AI 代码编辑器，官网地址为https://www.cursor.com/，直接在官网下载安装即可，基于VS Code二次开发而来，之所以没有采用插件方式，在官方网站上给出的答案是某些功能插件无法实现，产品专注在使用AI来进行编程方面，价格方面还不便宜，Pro单月20刀，企业版单月单…
阅读更多...
在 Vue 2 项目中使用 Element UI

在 Vue 2 项目中使用 Element UI

在 Vue 2 项目中使用 Element UI 本实验手册将指导你如何在 Vue 2 项目中使用 Element UI 组件库，搭建一个简单的页面。 一、介绍 Element UI Element UI （Element - 网站快速成型工具）是一套基于 Vue 2.0 的桌面端组件库，提供了丰富的、可复用的 UI 组件，可以帮助开发者快…
阅读更多...
『模拟赛』多校A层冲刺NOIP2024模拟赛18

『模拟赛』多校A层冲刺NOIP2024模拟赛18

『模拟赛记录』多校A层冲刺NOIP2024模拟赛18Rank 打成大奋了A. 选彩笔（rgb） 签 我是彩笔 赛时完全不会啊，打了一个 25k 的贪心结果爆栈了喜提 0pts。 最大值最小，还是二分答案。二分的答案是最大差，发现值域很小，我们在 check 时可以直接枚举每个色号的最大值，统计在所选…
阅读更多...
读UCOS源码总结

读UCOS源码总结

在之前一直想阅读一个RTOS的源码来看看里面到底是怎么设计的，虽说经常使用RTOS大概知道里面各个模块的工作原理，但是具体是如何实现的，从来没有看过。那么，初看代码当然要先找个简单的入门，于是，UCOSIII就成了我的选择。 以前啃源码的方式真的效率很低，看的头大速度还慢…
阅读更多...
多校A层冲刺NOIP2024模拟赛18

多校A层冲刺NOIP2024模拟赛18

赛时电脑死了，恼了就没交。赛后交是155pts。 T1 是二分答案+三维前缀和check，T2 瞎写了个搜索。 T1 选彩笔（rgb） 将r,g,b看做三个维度。 答案显然有可二分性，直接二分答案。那么就转化为是否存在一个边长为\(mid\)三维正方体，其内部有大于\(k\)个点。 三维前缀和维护即刻…
阅读更多...
# 20222309 2024-2025-1 《网络与系统攻防技术》实验四实验报告

# 20222309 2024-2025-1 《网络与系统攻防技术》实验四实验报告

1.实验内容 一、恶意代码文件类型标识、脱壳与字符串提取 对提供的rada恶意代码样本，进行文件类型识别，脱壳与字符串提取，以获得rada恶意代码的编写作者，具体操作如下： （1）使用文件格式和类型识别工具，给出rada恶意代码样本的文件格式、运行平台和加壳工具； （2）使用…
阅读更多...
从0开始搭建自己的直播平台

从0开始搭建自己的直播平台

本文讲述了如何从0开始，利用腾讯云的平台，快速搭建一个直播平台的过程。本文讲述了如何从0开始，利用腾讯云的平台，快速搭建一个直播平台的过程。 准备工作 要有两个已经备案完成的域名。 域名申请及备案的操作，这部分可以直接看腾讯云的文档，也可以等我后面有时间自己再写…
阅读更多...
[Zer0pts2020]easy strcmp

[Zer0pts2020]easy strcmp

[Zer0pts2020]easy strcmp die查壳找到加密函数如何找到加密函数的找到init函数，跟进funcs_889 、跟进使用x交叉引用qword_201090即可找到主加密函数 那这个加密函数是如何连上main函数的呢？ mainmain函数这里运用了strcmp，但我们却找不到strcmp到底对比了什么 但根据我们刚…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023