1/定义
- 在同一平面内,有一组邻边相等的平行四边形是菱形
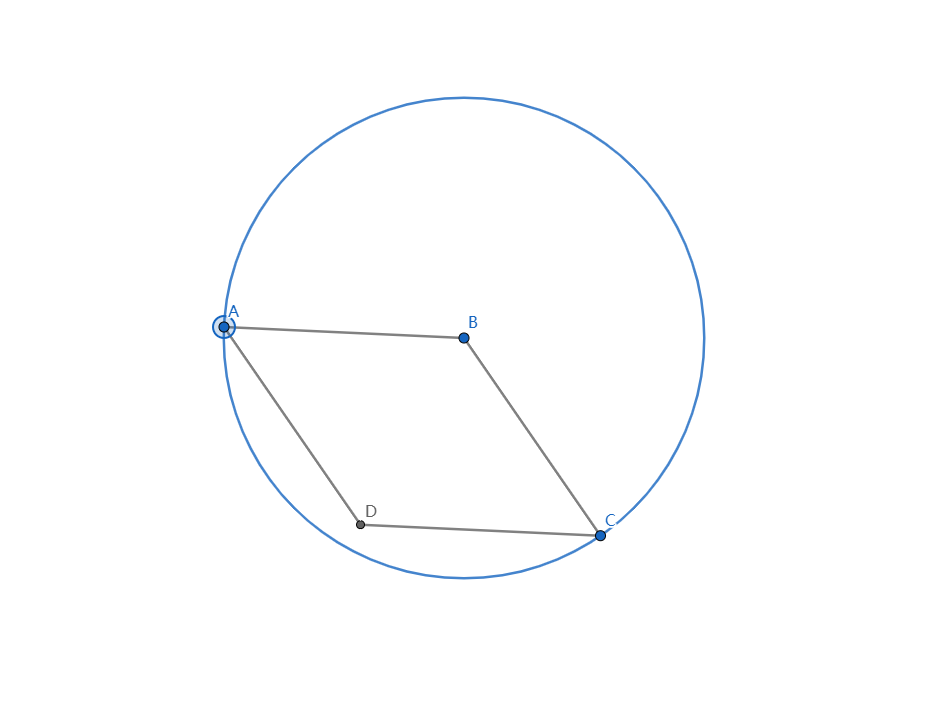
如图,四边形 \(ABCD\) 是一个菱形
2/性质
首先,在平行四边形原有的基础上,菱形还有一些特有的性质:
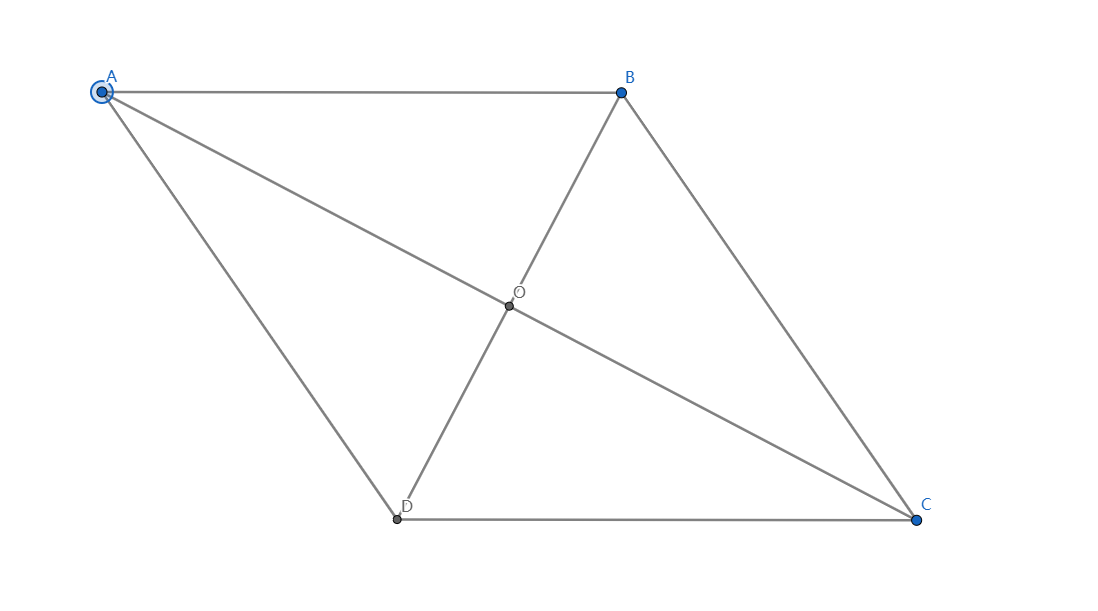
-
对角线互相垂直
\(\because \text{平行四边形}ABCD\)
\(\therefore AO = OC, BO = OD\)
\(\because AB = BC\)
\(\therefore \triangle ABC \text{为等腰直角三角形}\)
\(\therefore BO \bot AC\)
\(\therefore BD \bot AC\) -
四条边相等
\(\because \text{平行四边形}ABCD\)
\(\therefore AB = DC, AC = BD\)
\(\because AB = BC\)
\(\therefore AB = BC = DC = AD\)
3/判定
-
定义判定:略
-
四边相等
\(\because\text{易证} \triangle ADC \simeq \triangle CBA\)
\(\therefore \angle BAC =\angle ACD\)
\(\therefore AB \parallel DC\)
\(\therefore \text{四边形} ABCD \text{是平行四边形}\)
\(\therefore \text{符合菱形定义}\) -
对角线互相垂直平分:略
好的,完了