P10972 I-Country 题目分析

P10972 I-Country 题目分析

题目链接

分析题目性质

观察题目，可以发现的是一个凸多边形一定满足：

• 每一行的左端点列号先递减后递增。
• 每一行的右端点列号先递增后递减。

我们可以以此想到线性 \(dp\)。

思路

根据上述，我们需要关注以下的信息：

• 当前的左端点。

• 当前的右端点。

• 这一行以左端点开始连续选多少个。

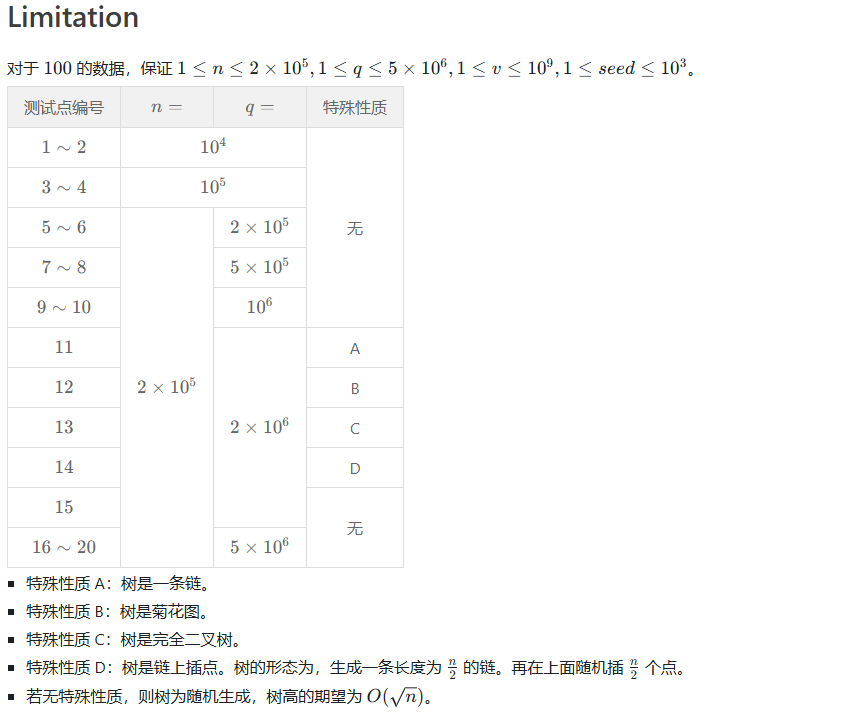
• 当前左端点列号需要满足的单调性。

• 当前右端点列号需要满足的单调性。

显然的，右端点、左端点和选的格子数知道两个就可确定第三个的值。

因此我们设：\(f_{i,j,l,r,0/1,0/1}\) 表示前 \(i\) 行已经处理完毕加上第 \(i\) 行有 \(j\) 个格子，第 \(i\) 行选择第 \(l\) 到 \(r\) 的格子，且左端点、右端点列号满足现在该有的单调性的最大价值（其中 \(0\) 表示递减，\(1\) 表示递增）。

考虑分类讨论，以下令 \(t=\sum_{w=l}^r a_{i,w},lst=j-(r-l+1)\)。

• 两边扩张状态：
  • \(f_{i,j,l,r,1,0}=t+\max_{l\leq l_2\leq r_2\leq r}\{f_{i-1,lst,l_2,r_2,1,0}\}.\)
• 左边扩张，右边收缩：
  • \(f_{i,j,l,r,1,1}=t+\max_{l\leq l_2\leq r\leq r_2}\left\{\max_{p_2\in[0,1]}\left\{f_{i-1,lst,l_2,r_2,1,p_2}\right\}\right\}.\)
• 左边收缩，右边扩张：
  • \(f_{i,j,l,r,0,0}=t+\max_{l_2\leq l\leq r_2\leq r}\left\{\max_{p_1\in[0,1]}\left\{f_{i-1,lst,l_2,r_2,p_1,0}\right\}\right\}.\)
• 两边收缩状态：
  • \(f_{i,j,l,r,0,1}=t+\max_{l_2\leq l\leq r\leq r_2}\left\{\max_{p_1\in[0,1]}\left\{\max_{p_2\in[0,1]}\left\{f_{i-1,lst,l_2,r_2,p_1,p_2}\right\}\right\}\right\}.\)

对于路径只需要记录当前状态的决策点即可，记得初始化一些必要的变量。

代码如下：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <stdlib.h>
#include <cstring>
#define N 20
using namespace std;
int n,m,K,a[N][N],sum[N][N];
struct node{int val;int prej,prel,prer;bool type1,type2;//to find the last.void init() {val = prej = prel = prer = 0;type1 = type2 = 0;}bool operator<(const node&adv) const {return val < adv.val;}
}f[N][N * N][N][N][2][2];
void debug(int i,int j,int l,int r,int typ1,int typ2) {printf("---------------- For %d %d %d %d %d %d --------------------\n",i,j,l,r,typ1,typ2);node t = f[i][j][l][r][typ1][typ2];cout << t.val << ' ' << t.prej << ' ' <<t.prel << ' ' << t.prer << ' ' << t.type1 <<' ' << t.type2 << endl;printf("----------------- END ---------------------\n");
}
signed main(){cin >> n >> m >> K;for (int i = 1;i <= n;i ++)for (int j = 1;j <= m;j ++)cin >> a[i][j];for (int i = 1;i <= n;i ++)for (int j = 1;j <= K;j ++)for (int l = 1;l <= m;l ++) for (int r = l;r <= m && r - l + 1 <= j;r ++){int t = 0,lst = j - (r - l + 1);for (int times = l;times <= r;times ++) t += a[i][times];
//					cout << lst <<' ' << t <<endl;node mx;mx.init();//以下的转移都是按照题解上面的转移顺序写的for (int l2 = l;l2 <= r;l2 ++)for (int len = 1;l2 + len - 1 <= r && len <= lst;len ++) {int r2 = l2 + len - 1;//						mx = max(mx,f[i - 1][lst][l2][r2][1][0]);if (mx < f[i - 1][lst][l2][r2][1][0])mx = {f[i - 1][lst][l2][r2][1][0].val,lst,l2,r2,1,0};}f[i][j][l][r][1][0] = mx,f[i][j][l][r][1][0].val += t;mx.init();for (int l2 = l;l2 <= r;l2 ++)for(int r2 = r;r2 - l2 + 1 <= lst && r2 <= m;r2 ++) {//						mx = max(mx,f[i - 1][lst][l2][r2][1][0]),//						mx = max(mx,f[i - 1][lst][l2][r2][1][1]);if (mx < f[i - 1][lst][l2][r2][1][0])mx = {f[i - 1][lst][l2][r2][1][0].val,lst,l2,r2,1,0};if (mx < f[i - 1][lst][l2][r2][1][1])mx = {f[i - 1][lst][l2][r2][1][1].val,lst,l2,r2,1,1};}f[i][j][l][r][1][1] = mx,f[i][j][l][r][1][1].val += t;mx.init();for (int l2 = 1;l2 <= l;l2 ++)for (int r2 = l;r2 <= r && r2 - l2 + 1 <= lst;r2 ++){//						mx = max(mx,f[i - 1][lst][l2][r2][0][0]),//						mx = max(mx,f[i - 1][lst][l2][r2][1][0]);if (mx < f[i - 1][lst][l2][r2][0][0])mx = {f[i - 1][lst][l2][r2][0][0].val,lst,l2,r2,0,0};if (mx < f[i - 1][lst][l2][r2][1][0])mx = {f[i - 1][lst][l2][r2][1][0].val,lst,l2,r2,1,0};}f[i][j][l][r][0][0] = mx,f[i][j][l][r][0][0].val += t;mx.init();for (int l2 = 1;l2 <= l;l2 ++)for (int r2 = r;r2 <= m && r2 - l2 + 1 <= lst;r2 ++)for (int p1 = 0;p1 < 2;p1 ++)for (int p2 = 0;p2 < 2;p2 ++)if (mx < f[i - 1][lst][l2][r2][p1][p2])mx = {f[i - 1][lst][l2][r2][p1][p2].val,lst,l2,r2,p1,p2};f[i][j][l][r][0][1] = mx,f[i][j][l][r][0][1].val += t;//					debug(i,j,l,r,0,0),debug(i,j,l,r,0,1),debug(i,j,l,r,1,0),debug(i,j,l,r,1,1);}node ans;ans.init();int sl = 0,sr = 0,si = 0;for (int i = 1;i <= n;i ++)for (int l = 1;l <= m;l ++)for (int r = l;r - l + 1 <= K && r <= m;r ++)for (int p1 = 0;p1 < 2;p1 ++)for (int p2 = 0;p2 < 2;p2 ++)if (ans < f[i][K][l][r][p1][p2])ans = f[i][K][l][r][p1][p2],sl = l,sr = r,si = i;cout << "Oil : " << ans.val << endl;int fc = K;for (;fc;) {for (int i = sl;i <= sr;i ++) cout << si << ' ' << i << endl,fc --;sl = ans.prel,sr = ans.prer,si --;ans = f[si][fc][sl][sr][ans.type1][ans.type2];}return 0;
}

总结：为了实现转移的必要，我们有时候会有多维的 \(dp\) 状态。