SS241112A. 定向越野（walk）

SS241112A. 定向越野（walk）

题意

给你 \(n\) 个点，\(n \le 12\)，你可以从任意一个点出发以任意顺序依次遍历所有点燃火回到起点，你只能拐直角走，问最小路程。答案输出最小路程的平方，输出分数形式。可以证明最小路程的平方一定是有理数。

思路

显然枚举遍历顺序。

首先需要明白为什么答案一定是有理数。

感觉我们的初始方向必须是某一个向量的方向，假设这个是正确的。

考虑起点初始方向是 \(\alpha\)，我们可以把整个图旋转 \(\alpha\)，这样相当于我们只能往坐标轴方向走。

考虑旋转后每个点的坐标，起点是 \((0,0)\)，第一个经过的点是 \((len_{0,1},0)\)（其中 \(len_{u,v}\) 表示点 \(u\) 和点 \(v\) 的直线距离）。每个点与原点连线，相当于这条线的角度减去 \(\alpha\)。设这条线的角度是 \(\beta\)，\(\alpha\) 和 \(\beta\) 的 \(\tan\) 都是有理数，已知。那么就可以求出 \(\beta-\alpha\) 的 \(\tan\) 了，也是有理数。

不记得三角函数公式……

\[\sin (\beta-\alpha)=\sin \beta \cos \alpha - \cos \beta \sin \alpha\\ \cos (\beta-\alpha)=\sin \beta \cos \alpha + \cos \beta \sin \alpha\\ \tan (\beta-\alpha)=\frac{\tan \beta - \tan \alpha}{1- \tan \beta \tan \alpha} \]

我们要证明答案只含一种无理数，否则如果是多个无理数相加，平方后仍然是无理数。

也就是证明答案仅含有 \(len(1,2)\) 一种或零种无理数。

点 \(u\) 的坐标 \(x_u=\cos x \cdot len_{1,u},y_u=\sin x \cdot len(1,u)\)，展开后因为 \(\sin x,\cos x\) 分母里本身有一个 \(len_{1,u}\)，因此就消掉了 \(len_{1,u}\)，只剩下一个有理数乘（其实是除啦） \(len(1,2)\) 了。

证毕。

回到最初的假设，事实上这个结论是正确的。我不会证明。想象一个等腰直角三角形，最优的路径是以底边为初始方向，你发现虽然你微调初始方向后上边底边的路变长，上面的路变短，但是这是不优的。因此大胆猜测结论正确？

关键是如果没有这个结论，你没法做啊。所以结论是对的。。。

题解写得挺好。

在计算器上画出 \(y=\sin x + \cos x\) 函数图像。

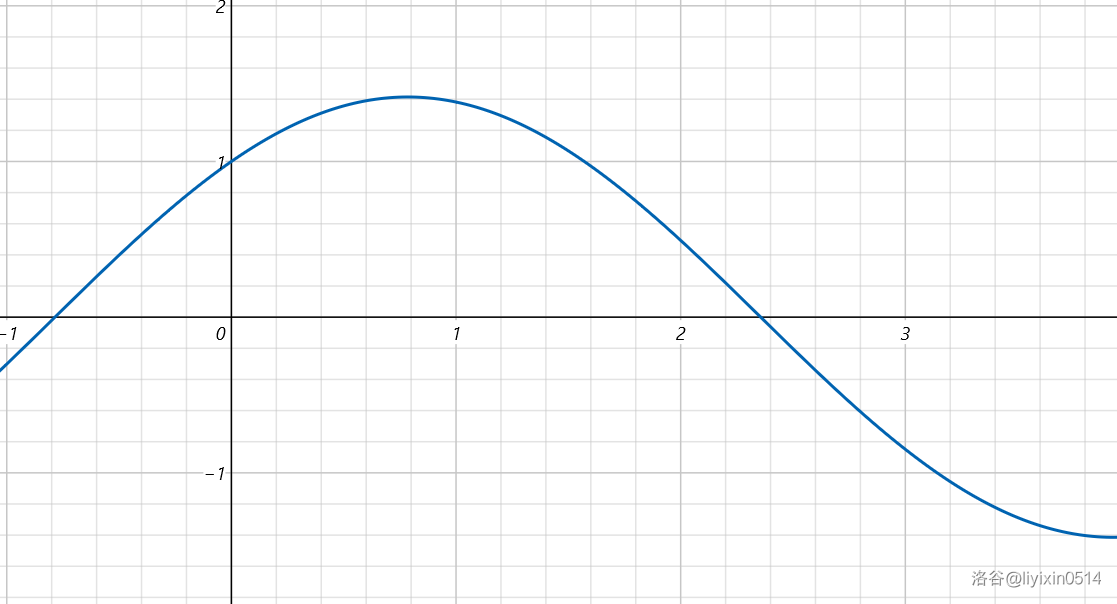
长这样。其实应该是 \(y=\sin x + \cos x\)：

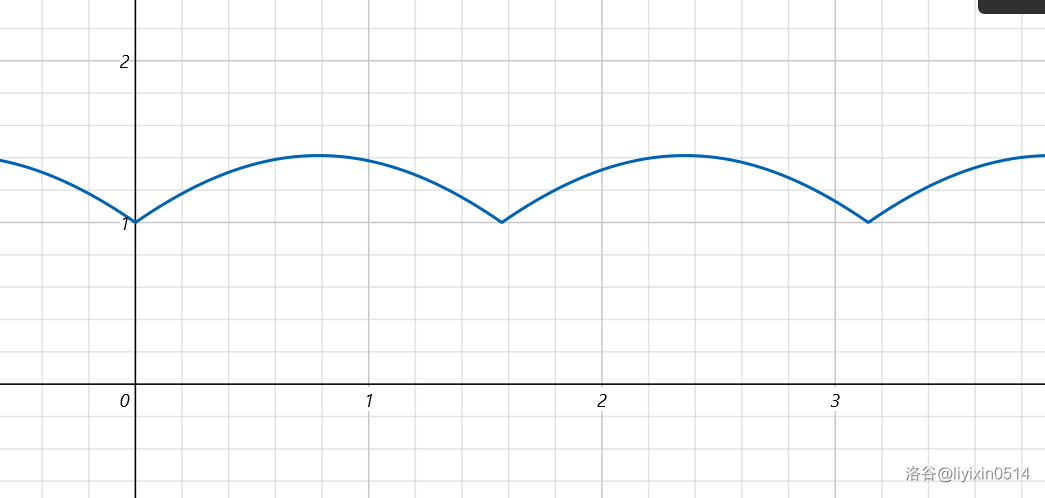
这是个分段的凸函数，当 \(x=0\) 的时候取得最小值。所以它们加起来的最小值一定是在某个 \(x=0\) 的位置取到，因为如果你取其他位置，一定可以选择旁边的位置使答案更小。

我觉得很难理解。容易想错。只是给出结论再去证明是相对好感性理解的。

嗯没了。

直接枚举遍历顺序是阶乘的，可以状压 DP，状态是初始方向，哪些点已经经过，最后一个点是什么，其中初始方向可以循环数组，时间 \(O(n^3 2^n)\)，空间 \(O(n 2^n)\)，转移枚举下一个点，总时间是 \(O(n^4 2^n)\)。