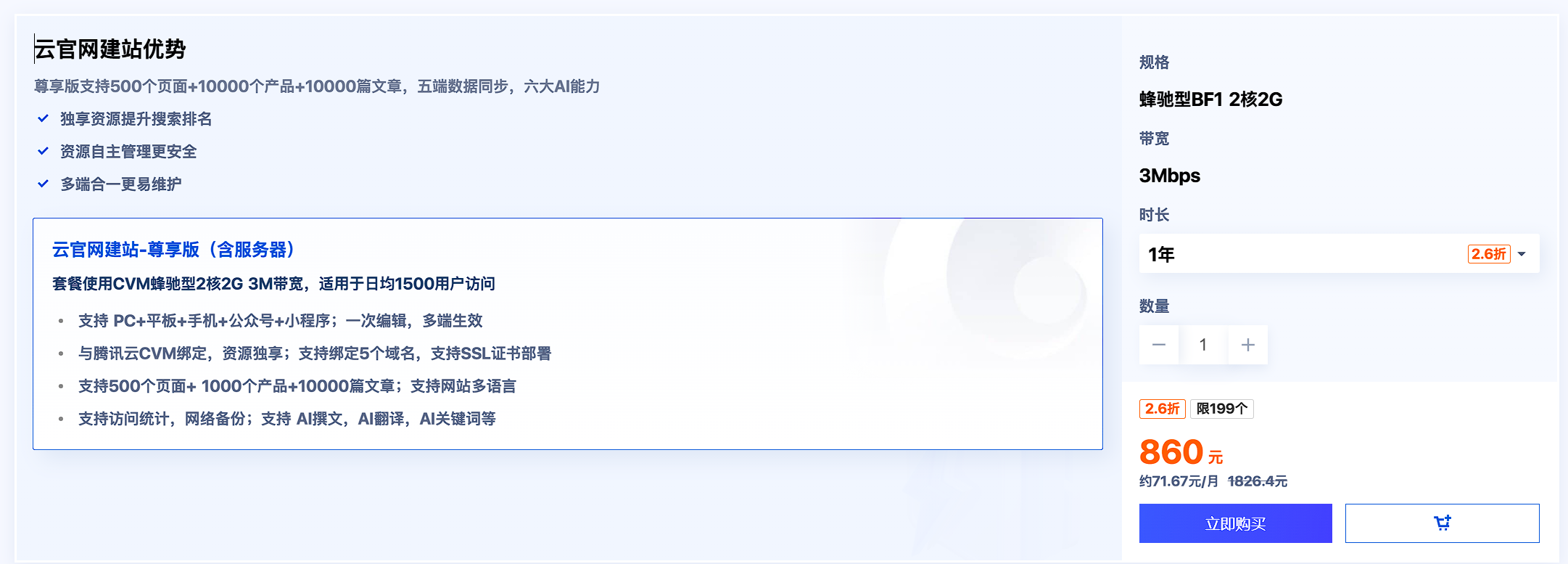
Darboux 定理:如果函数 \(f\) 在开区间 \(I\) 上有定义并且可微,\([a,b]\subset I\),则 \(f'(x)\) 在 \([a,b]\) 上取遍 \(f'(a)\) 与 \(f'(b)\) 之间的一切值。
证明:若 \(f'(a)=f'(b)\),定理自然成立,下令 \(f'(a)<f'(b)\). (\(f'(a)>f'(b)\) 的情况同理)
任取 \(\eta\in (f'(a),f'(b))\),令 \(g(x):=f(x)-\eta x,x\in I\),则 \(g'(a)<0\) 且 \(g'(b)>0.\) 因此存在 \(x_1,x_2\in (a,b)\),使得 \(g(x_1)<g(a),g(x_2)<g(b)\).
因为 \(g(x)\) 在 \([a,b]\) 上连续,所以 \(g\) 在 \([a,b]\) 上存在最小值,令 \(m=g(x_0),x\in [a,b]\) 是 \(g\) 在 \([a,b]\) 上的最小值,则 \(g(x_0)\le g(x_1)<g(a)\),因此 \(x_0\ne a\),同理 \(x_0\ne b\),从而 \(x_0\in (a,b).\)
由费马引理得 \(g'(x_0)=0\),即 \(f'(x_0)=\eta.\) 从而 \(f'(x)\) 在 \([a,b]\) 上取遍 \(f'(a)\) 与 \(f'(b)\) 之间的一切值.
接下来我们介绍 Darboux 定理的几个推论.
若 \(f\) 是 \(\mathbb R\) 上的可微函数,则 \(f'\) 不存在第一类间断点.
证明:任取实数 \(x_0\),若 \(f'(x_0-)\)
存在,假设 \(f'(x_0-)\ne f'(x_0)\).
不妨令 \(f'(x_0-)<f'(x_0)\),令 \(\varepsilon=\dfrac{f'(x_0)-f'(x_0-)}{2}>0\),则存在 \(\delta>0\),使得当 \(x\in (x_0-\delta,x_0)\) 时有 \(f'(x)<f'(x_0-)+\varepsilon<f'(x_0)\). 任取 \(x_1\in (x_0-\delta,x_0)\),则 \(f'(x)\) 在 \([x_1,x_0]\) 上无法取得 \((f'(x_0-)+\varepsilon,f'(x_0))\) 中的值,与 Darboux 定理矛盾.
因此只要 \(f'(x_0-)\) 存在则必有 \(f'(x_0-)=f'(x_0)\). 同理,只要 \(f'(x_0+)\) 存在则必有 \(f'(x_0+)=f'(x_0)\). 即 \(f'\) 不存在第一类间断点.
若 \(f\) 是 \(\mathbb R\) 上的可微函数,则 \(f'\) 不存在无穷间断点.
证明:任取实数 \(x_0\in\mathbb R\),假设 \(f'(x_0-)=\infty\).
不妨令 \(f'(x_0-)=+\infty\),取 \(A>f'(x_0)\),则存在 \(\delta>0\) 使得当 \(x\in(x_0-\delta,x_0)\) 时有 \(f'(x)>A\). 任取 \(x_1\in (x_0-\delta,x_0)\),则 \(f'(x)\) 在 \([x_1,x_0]\) 上无法取得 \((f'(x),A)\) 中的值,这与 Darboux 定理矛盾.
因此 \(f'(x_0-)\ne \infty\),从而 \(\lim\limits_{x\rightarrow x_0}f'(x)\ne \infty\),即 \(f'\) 不存在无穷间断点.
若 \(f\) 在开区间 \(I\) 上有定义且可微,且在 \((a,b)\subset I\) 上 \(f''(x)\) 存在,若 \(f'(a)=f'(b)\),则存在 \(\xi\in (a,b)\),使得 \(f''(\xi)=0.\)
证明:若存在 \((a,b)\) 内的不同的两点 \(x_1,x_2\) 满足 \(f''(x_1)\le 0,f''(x_2)\ge 0\),则由 Darboux 定理,存在 \(x_1,x_2\) 之间的点 \(\xi\) 使得 \(f''(\xi)=0\),当然 \(\xi\in (a,b)\).
否则,要么 \(f''(x)\) 在 \((a,b)\) 上恒正或恒负,不妨令 \(f''(x)\) 在 \((a,b)\) 上恒正,则 \(f'\) 在 \((a,b)\) 上严格单增.
从而 \(f'(b-)=\sup\limits_{x\in (a,b)}f'(x)\),由前两个推论的证明过程得 \(f'(b)=\sup\limits_{x\in (a,b)} f'(x)\),同理 \(f'(a)=\inf\limits_{x\in (a,b)} f'(x)\). 从而 \(f'(a)<f'(b)\),矛盾!
综上,必存在 \(\xi\in (a,b)\),使得 \(f''(\xi)=0\).
若 \(f\) 在开区间 \(I\) 上有定义且可微,且在 \((a,b)\subset I\) 上 \(f''(x)\) 存在,则存在 \(\xi\in (a,b)\),使得 \(f'(b)-f'(a)=f''(\xi)(b-a)\).
令 \(g(x):=f(x)-\dfrac{1}{2}\dfrac{f'(b)-f'(a)}{b-a}(x-a)^2,x\in I\),则 \(g\) 可微,且
易见 \(g'(a)=f'(a)=g'(b)\),且 \(g''\) 在 \((a,b)\) 上存在. 由上一条推论得,存在 \(\xi\in (a,b)\),使得 \(g''(\xi)=0\),即 \(f'(b)-f'(a)=f''(\xi)(b-a)\).