录制唱片
你刚刚继承了流行的 “破锣摇滚” 乐队录制的尚未发表的 \(N\)(\(1\leq N\leq 20\))首歌的版权。你打算从中精选一些歌曲,发行 \(M\)(\(1\leq M\leq 20\))张 CD。每一张 CD 最多可以容纳 \(T\)(\(1\leq T\leq 20\))分钟的音乐,一首歌不能分装在两张 CD 中。CD 数量可以用完,也可以不用完。
不巧你是一位古典音乐迷,不懂如何判定这些歌的艺术价值。于是你决定根据以下标准进行选择:
-
1.歌曲必须按照创作的时间顺序在所有的 CD 盘上出现。(注:第 \(i\) 张盘的最后一首的创作时间要早于第 \(i+1\) 张盘的第一首)
-
2.选中的歌曲数目尽可能地多。
f[i][j][k]表示第i个CD,现在取到了第j首歌,此CD已存k分钟的歌了。
for(int i=0;i<m;i++){//枚举CDfor(int j=1;j<=n;j++){//枚举所选的歌for(int k=0;k+a[j]<=t;k++){//枚举此CD已经存了多少分钟for(int l=j-1;l>=0;l--){//枚举上一个CD取到了哪for(int c=0;c<=t;c++){f[i+1][j][k+a[j]]=max(f[i+1][j][k+a[j]],f[i][l][c]+1);}//第一种情况,这个CD还没用过。f[i+1][j][k+a[j]]=max(f[i+1][j][k+a[j]],f[i+1][l][k]+1);//第二种情况,这个CD已用了k分钟。ss=max(ss,f[i+1][j][k+a[j]]);//时刻更新最大值。}}}}
路短最
你可以通过许多的算法找到从一个地方到另外一个地方的最短路径。人们在他们的车上安装 GPS 设备然后他们的手机告诉他们最快的到达目的地的方式。然而,当在假期时,Troy 喜欢慢慢旅游。他想找最长的到目的地的路径以便他可以在路途中看许多新的以及有趣的地方。
因此,一个有效的路径包含一个不同城市的序列 \(c_1,c_2,...,c_k\),并且对于每个 \(1\le i<k\),有道路从 \(c_i\) 通往 \(c_{i+1}\)。
他不想重复访问任何城市,请帮他找出最长路径。
对于 \(100\%\) 的数据,有 \(2\le n \le 18,\) \(1\le m \le n^2-n,\) \(0\le s,d \le n-1,\) \(s\neq d,\) \(1\le l\le 10000\)。
明显可以状压,把每个城市的访问状态压到一位,Fij存i状态时在j城市的最长路。
Cloakroom
有 \(n\) 件物品,每件物品有三个属性 \(a_i, b_i, c_i\ (a_i<b_i)\)。注意输入顺序为 \(c_i, a_i, b_i\)。
再给出 \(q\) 个询问,每个询问由非负整数 \(m, k, s\) 组成,问是否能够选出某些物品使得:
- 对于每个选的物品 \(i\),满足 \(a_i\le m\) 且 \(b_i>m+s\)。
- 所有选出物品的 \(c_i\) 的和正好是 \(k\)。
\(1\le n\le 1000\),\(1\le a_i<b_i\le 10^9\),\(1\le c_i\le 1000\)。
\(1\le q\le 10^6\),\(1\le m\le 10^9\),\(1\le k\le 10^5\),\(0\le s\le 10^9\)。
把询问离线下来,把物品按a排序,询问按m排序。Fk表示当前考虑的物品c和恰好为k时的b被最大化的最小值。
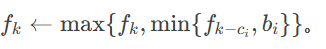
神仙状态,反正我想不出来。
#include<bits/stdc++.h>
#define int long long
#define inf 9000000000000000000
using namespace std;
struct S{int a, b, c;
} a[1050];
constexpr int maxn = 2e6+10;
struct Q{int m, k, s, i;
} q[maxn];
int n, m, f[maxn];
bool b[maxn];
bool cmp1(S x, S y) { return x.a < y.a; }
bool cmp2(Q x, Q y) { return x.m < y.m; }
signed main(){scanf("%lld", &n);for (int i = 0; i < n; ++i)scanf("%lld%lld%lld", &a[i].c, &a[i].a, &a[i].b);sort(a, a + n, cmp1);scanf("%lld", &m);for (int i = 0; i < m; ++i)scanf("%lld%lld%lld", &q[i].m, &q[i].k, &q[i].s), q[i].i = i;sort(q, q + m, cmp2);f[0] = inf;for (int i = 0, j = 0; i < m; ++i){for (; j < n && a[j].a <= q[i].m; ++j)for (int l = 1e5; l >= a[j].c; --l)f[l] = max(f[l], min(f[l - a[j].c], a[j].b));b[q[i].i] = f[q[i].k] > q[i].m + q[i].s;}for (int i = 0; i < m; ++i)puts(b[i] ? "TAK" : "NIE");return 0;
}
奶牛看电影
奶牛贝西想连续看 \(L\)(\(1 \le L \le 10^8\))分钟的电影,有 \(N\)(\(1 \le N \le 20\))部电影可供选择,每部电影会在一天的不同时段放映。
贝西可以在一部电影播放过程中的任何时间进入或退出放映厅。但她不愿意重复看到一部电影,所以每部电影她最多看到一次。她也不能在看一部电影的过程中,换到另一个正在播放相同电影的放映厅。
请帮贝西计算她能够做到从 \(0\) 到 \(L\) 分钟连续不断地观看电影,如果能,请计算她最少看几部电影就行了。
来不及实现了,先写思路。
一眼状压,发现不会了。
考虑看题解。
状态是1e6的,显然压不进去别的东西了,而且最优解已经在状态里了。
所以我们dp里存另一个要最优化的东西。Fi表示状态为i时最晚的结束时间,我们要最化这个东西。显然转移的时候可以二分到没有空隙的最近一场即将开始的电影一定是最优的。