先来看一道大家基本都能默写出来的题目:
您需要写一种数据结构(可参考题目标题),来维护一些数,其中需要提供以下操作:
- 插入一个数 \(x\)。
- 删除一个数 \(x\)(若有多个相同的数,应只删除一个)。
- 定义排名为比当前数小的数的个数 \(+1\)。查询 \(x\) 的排名。
- 查询数据结构中排名为 \(x\) 的数。
- 求 \(x\) 的前驱(前驱定义为小于 \(x\),且最大的数)。
- 求 \(x\) 的后继(后继定义为大于 \(x\),且最小的数)。
很显然,我们需要手写一个 Treap。就像这样:
//代码是盒的,别用qwq
#include<cstdio>
using namespace std;
#define MAXN 1000000
int f[MAXN],cnt[MAXN],value[MAXN],sons[MAXN][2],sub_size[MAXN],whole_size,root;
inline int qread(){int res=0,k=1;char c=getchar();while(!isdigit(c)){if(c=='-')k=-1;c=getchar();}while(isdigit(c)){res=(res<<1)+(res<<3)+c-48;c=getchar();}return res*k;
}
inline void S_Clear(int x){sons[x][0]=sons[x][1]=f[x]=sub_size[x]=cnt[x]=value[x]=0;
}
inline bool get_which(int x){return sons[f[x]][1]==x;
}
inline void update(int x){if (x){ sub_size[x]=cnt[x]; if (sons[x][0]) sub_size[x]+=sub_size[sons[x][0]]; if (sons[x][1]) sub_size[x]+=sub_size[sons[x][1]]; } return ;
}
inline void rotate(int x){int father=f[x],g_father=f[father],which_son=get_which(x);sons[father][which_son]=sons[x][which_son^1];f[sons[father][which_son]]=father;sons[x][which_son^1]=father;f[father]=x;f[x]=g_father;if(g_father){sons[g_father][sons[g_father][1]==father]=x;}update(father);update(x);
}
inline void splay(int x){for (int fa;fa=f[x];rotate(x)) if (f[fa]) rotate((get_which(x)==get_which(fa))?fa:x); root=x;
}
inline void insert(int x){if(!root){whole_size++;sons[whole_size][0]=sons[whole_size][1]=f[whole_size]=0;root=whole_size;sub_size[whole_size]=cnt[whole_size]++;value[whole_size]=x;return ;} int now=root,fa=0;while(1){if(x==value[now]){cnt[now]++;update(now);update(fa);splay(now);break;}fa=now;now=sons[now][value[now]<x];if(!now){whole_size++;sons[whole_size][0]=sons[whole_size][1]=0;f[whole_size]=fa;sub_size[whole_size]=cnt[whole_size]=1;sons[fa][value[fa]<x]=whole_size;value[whole_size]=x;update(fa);splay(whole_size);break; }}}
inline int find_num(int x){ int now=root;while(1){if(sons[now][0]&&x<=sub_size[sons[now][0]])now=sons[now][0];else {int temp=(sons[now][0]?sub_size[sons[now][0]]:0)+cnt[now];if(x<=temp)return value[now];x-=temp;now=sons[now][1];}}
}inline int find_rank(int x){int now=root,ans=0; while(1){ if (x<value[now]) now=sons[now][0]; else{ ans+=(sons[now][0]?sub_size[sons[now][0]]:0); if (x==value[now]){ splay(now); return ans+1; } ans+=cnt[now]; now=sons[now][1]; } }
}
inline int find_pre(){int now=sons[root][0];while(sons[now][1])now=sons[now][1];return now;
}
inline int find_suffix(){int now=sons[root][1];while(sons[now][0])now=sons[now][0];return now;
}
inline void my_delete(int x){int hhh=find_rank(x);if (cnt[root]>1){cnt[root]--; update(root); return;} if (!sons[root][0]&&!sons[root][1]) {S_Clear(root);root=0;return;} if (!sons[root][0]){ int old_root=root; root=sons[root][1];f[root]=0; S_Clear(old_root); return; } else if (!sons[root][1]){ int old_root=root; root=sons[root][0]; f[root]=0; S_Clear(old_root); return; } int left_max=find_pre(),old_root=root; splay(left_max); sons[root][1]=sons[old_root][1]; f[sons[old_root][1]]=root; S_Clear(old_root); update(root);
}int main(){int m,num,be_dealt;cin>>m;for(int i=1;i<=m;i++){num=qread();be_dealt=qread();switch(num){case 1:insert(be_dealt);break;case 2:my_delete(be_dealt);break;case 3:printf("%d\n",find_rank(be_dealt));break;case 4:printf("%d\n",find_num(be_dealt));break;case 5:insert(be_dealt);printf("%d\n",value[find_pre()]);my_delete(be_dealt);break;case 6:insert(be_dealt);printf("%d\n",value[find_suffix()]);my_delete(be_dealt);break;}}return 0;
}
实际上写出这么多的代码需要极强的码力,而且容易出错在考场上红温。
直到有一天,你学会发布了这篇文章:
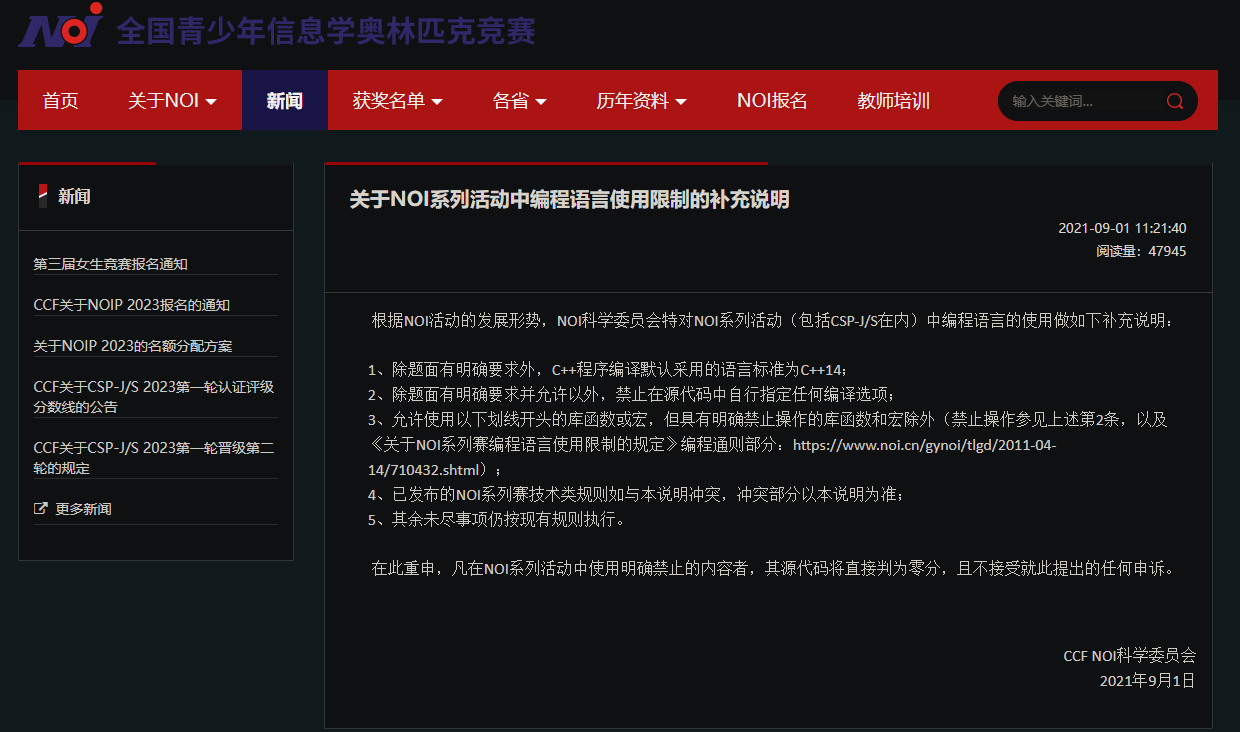
下划线开头的函数包括__gcd等,同时还包括一个神秘的库叫做 __gnu_pbds。这个库里面包括了很多数据结构,其中甚至包括平衡树,除此之外还有类似于哈希之类的东西,很大程度上可以减轻写代码的负担,但是注意,如果背不对模板,不要尝试在考场上使用。
先上代码:
#include<bits/stdc++.h>
#include<bits/extc++.h>
using namespace __gnu_pbds;
//using namespace std;
inline int read()
{int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0' && ch<='9')x=x*10+ch-'0',ch=getchar();return x*f;
}
inline void write(int x)
{if(x<0)putchar('-'),x=-x;if(x>9)write(x/10);putchar(x%10+'0');return;
}
const int inf = INT_MAX;
tree<std::pair<int,int>,null_type,std::less<std::pair<int,int> >,rb_tree_tag,tree_order_statistics_node_update>rbt;
int main()
{int n=read();for(int i=1;i<=n;i++){int opt=read(),val=read();if(opt==1){rbt.insert(std::make_pair(val,i));}else if(opt==2){rbt.erase(rbt.lower_bound(std::make_pair(val,0)));}else if(opt==3){write(rbt.order_of_key(std::make_pair(val,0))+1);putchar(10);}else if(opt==4){auto it=rbt.find_by_order(val-1);write((*it).first);putchar(10);}else if(opt==5){auto it=rbt.lower_bound(std::make_pair(val,0));write((*(--it)).first);putchar(10);}else{auto it=rbt.upper_bound(std::make_pair(val,inf));write((*(it)).first);putchar(10);}}return 0;
}
根据笔者实测,运行速度略高于所有通过代码的平均水平。
注意:上面的代码如果在devcpp里面打开是百分之百无法编译的,如图:
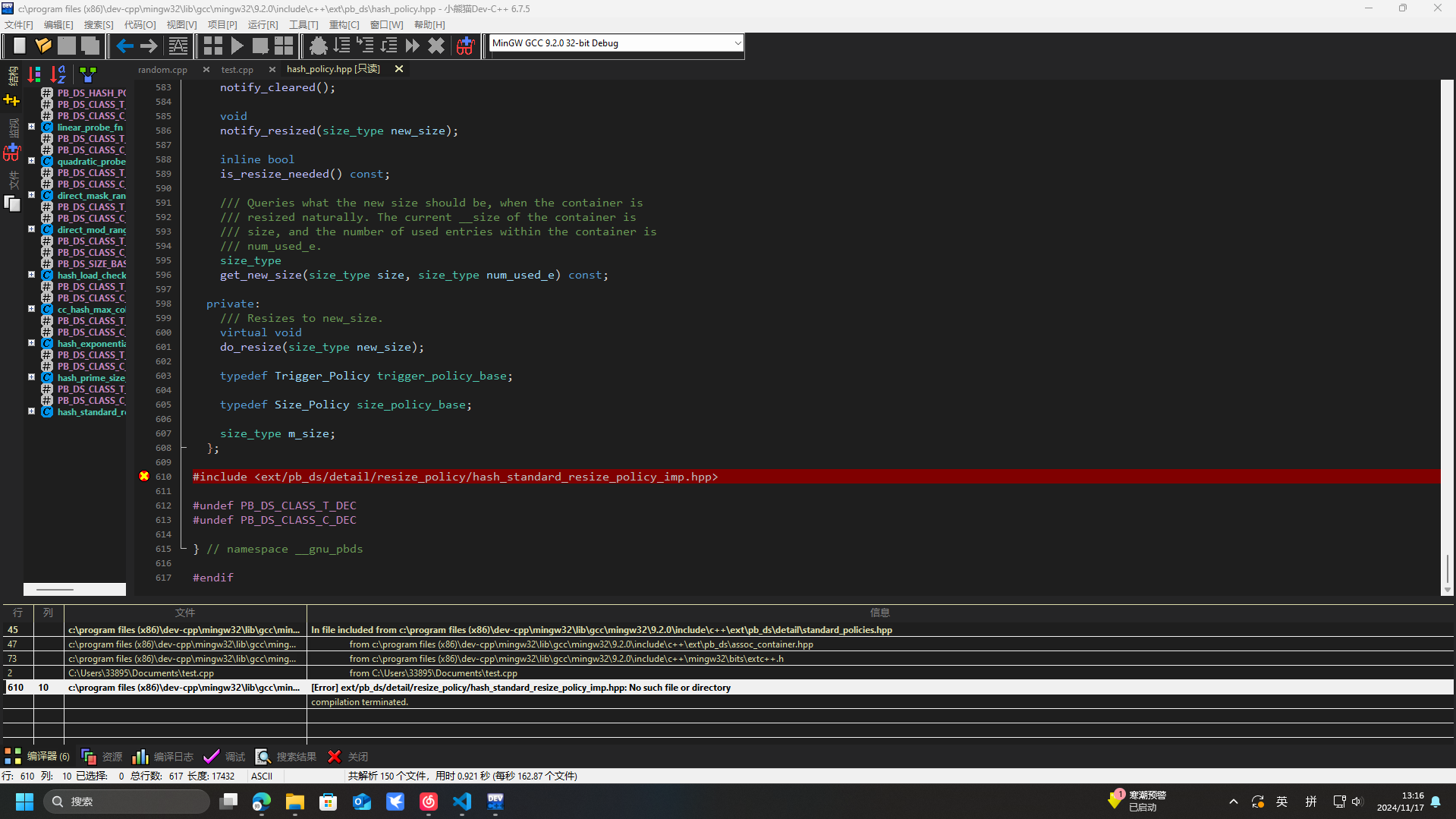
这个时候,如果是windows系统使用devcpp建议把devc++自带的mingw64编译器添加到系统环境变量后直接在cmd里面用这个命令编译:
g++ <yourfilename>.cpp -o <the_name_of_exe_file> -O2 -std=c++14
接着说模板的事情。
除了rb_tree之外平板电视里面还有treap和基于vector实现的平衡树,但是两种我都不建议使用,被卡过就知道为啥了。
除此之外还有哈希有关的东西,这样写,和map类似
cc_hash_table<int,bool> h;
gp_hash_table<int,bool> h;
其中下面那个稍微快一点。操作支持find操作和[]。然而这个好东西可以把 \(O(nlogn)\) 的复杂度直接拽到 \(O(n)\)。在考场上真的可以救你一命。

但是特别注意,使用了这个东西就不太建议引入using namespace std;了,因为可能会因为函数名称冲突见祖宗,建议实际考试或者模拟赛的时候在linux系统下编译一下试试再提交。简而言之,这个东西是你在考场上实在想不出来模板怎么写的时候最后的救命稻草。