介绍下自己的离奇思路:
先读清楚题意!要求是旋转等价,即两个以 \(c\) 个 \(1\) 开头,总 \(1\) 个数不超过 \(k+c\) 的字符串算一种。
那怎么刻画"只算一种"这个条件呢?一个想法可以是,对每个字符串赋一个权值,一种字符串的权值即旋转出来的每个合法的,把它们加起来应该是 \(1\),再全部加出来。
一个直接的赋权方式是,对一个最小循环节是 \(d(d|n)\) 的字符串,它的权值为 \(\dfrac{1}{\sum\limits_{i=1}^{d}ok_i}\),其中 \(ok_i\) 代表字符串是否可以以位置 \(i\) 开头。
然后做法就是枚举 \(d\),求出容斥系数,因为要考虑所有大小为 \(d\) 的 \(01\) 串,所以要 dp 三个量:长度,\(1\) 个数,以及合法开头点数。这样复杂度肯定没救了。
这是同学你可能会说:没必要让每个"合法点"都合法作为开头啊?我对于一个 \(len\geq c\) 的 \(1\) 段,要求上必须以这个段的段头作为开头才可以,这不就轻松了吗?
很好!这样就改为了段数分之一,不过还是要 dp 这个段数有点烦,怎么办呢?
其实这时候你可以发现,我们没有必要非去设它的所有合法轮换的权值都相等啊!只需要加起来是 \(1\) 就可以。于是容易想到,停时定理那个设权值的方式,即 \(\dfrac{a_i}{\sum a_k}\),换在这题也就是,目前一个段到下一个合法段的距离,除掉总长,也就是 \(d\)。而目前段就是 \(1\sim c\) 开头那个尽量延伸,且要求 \(s_d=0\),即必须要是一个段头。
这下我们就不需要考虑这个字符串整体了,只需要得到一个最前的合法段,钦定即可!
其实可以两种情况分开讨论:
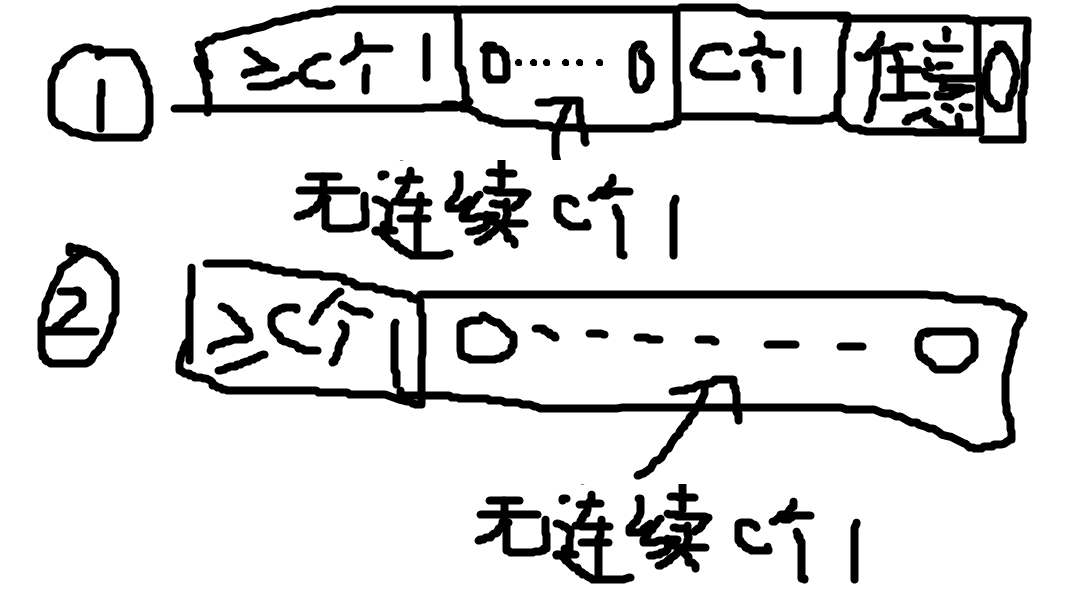
第一种情况的权值是 \(\dfrac{x-1}{d}\),其中 \(x\) 表示后面那个合法段的开头位置。第二种的权值就是 \(\dfrac{d}{d}=1\)。
显然情况一更难,我们只考虑这个咋求。不难发现,枚举 \(x\) 的位置,和 \(x\) 前面 \(0\) 的个数,就可以通过一些预处理做到除了预处理之外单次 \(O(d^2)\) 的复杂度。
那么预处理是什么呢?也不难,就是 \(f_{i,j}\) 表示长度为 \(i\),以 \(0\) 结尾,不能出现连续 \(c\) 个 \(1\) 的字符串数,则有转移:
其实这个甚至只用 \(+1\) 优化都可以做,完全不需要前缀和优化。不过其它一些预处理可能要前缀和优化,不过都很简单。这里是 \(O(n^2)\) 的。
最后一个小问题是我们枚举的是 \(d\),也就是钦定了有大小为 \(d\) 的循环节。注意,最小循环节一定整除其它的,所以容斥系数可以直接这么理解:
然后乘乘加加就可以了。复杂度是 \(O(n^2+\sum\limits_{d|n}d^2)=O(\sum\limits_{i\geq 1}\dfrac{n}{i}^2)=O(n^2)\)。
这是我的做法,代码如下,很短:
#include<bits/stdc++.h>
#define mod 1000000007
using namespace std;
int powdv(int x,int y=mod-2){int ans=1;while(y){if(y&1)ans=1ll*ans*x%mod;y>>=1,x=1ll*x*x%mod;}return ans;
}
int ff[3005],hh[3005];
int f[3005][3005],h[3005][3005];
int main(){int n,c,k;scanf("%d%d%d",&n,&c,&k);for(int d=n;d>=1;--d)if(n%d==0){ff[d]=powdv(d);for(int g=2*d;g<=n;g+=d)if(n%g==0){ff[d]=(ff[d]-ff[g]+mod)%mod;}}f[1][1]=1;for(int i=2;i<=n;++i)for(int j=2;j<=i;++j){f[i][j]=(f[i-1][j]+f[i-1][j-1])%mod;if(i>c+1)f[i][j]=(f[i][j]-f[i-c-1][j-1]+mod)%mod;}h[0][0]=1;for(int i=1;i<=n;++i)for(int j=0;j<=i;++j){h[i][j]=(h[i-1][j]+(j?h[i-1][j-1]:0))%mod;}for(int i=1;i<=n;++i)for(int j=i;j>=1;--j){h[i][j-1]=(h[i][j-1]+h[i][j])%mod;}int ans=0;for(int d=c+1;d<=n;++d)if(ff[d]){int mx=(k+c)/(n/d),gs=max(0,d-mx),he=0;for(int i=1;i<=d-c;++i)for(int j=gs;j<=i;++j){he=(he+1ll*d*f[i][j])%mod;}for(int i=1;i<=d;++i)hh[i]=0;for(int i=c+2;i<=d-c;++i){int ht=0;for(int j=1;j<=i;++j){hh[j]=(hh[j]+f[i-c-1][j])%mod;ht=(ht+1ll*hh[j]*h[d-c-i][max(0,gs-1-j)])%mod;}he=(he+1ll*(i-1)*ht)%mod;}ans=(ans+1ll*ff[d]*he)%mod;}if(k==n-c)ans=(ans+1)%mod;printf("%d\n",ans);return 0;
}
另外说说 Burnside 的做法,也是积累了一个套路:
------------------分割线--------------------
看了眼题解,怎么这么简单???我最开始的时候想用 Burnside,可是发现不完备,遂放弃。实际你仔细想想,发现我只要不要求必须以 \(c\) 个 \(1\) 开头就好了啊!!!!!只用这样一件事情:存在相邻 \(c\) 个字符全为 \(1\),之后就还是枚举循环节去 Burnside 就好了。思维难度少了 \(114514\) 倍,唉唉唉。