第八章习题

学号后四位:3018
8.4:

点击查看代码

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt# 定义微分方程组
def differential_equations(state, t):x, y = statedxdt = -x ** 3 - ydydt = x - y ** 3return [dxdt, dydt]# 设定初始条件
initial_conditions = [1, 0.5]# 定义时间范围
t = np.linspace(0, 30, 1000)# 求解微分方程组
solution = odeint(differential_equations, initial_conditions, t)
x_solution = solution[:, 0]
y_solution = solution[:, 1]# 绘制x(t)的解曲线
plt.subplot(2, 1, 1)
plt.plot(t, x_solution)
plt.xlabel('t')
plt.ylabel('x(t)')
plt.title('Solution Curve of x(t)')# 绘制y(t)的解曲线
plt.subplot(2, 1, 2)
plt.plot(t, y_solution)
plt.xlabel('t')
plt.ylabel('y(t)')
plt.title('Solution Curve of y(t)')# 在相平面上绘制轨线
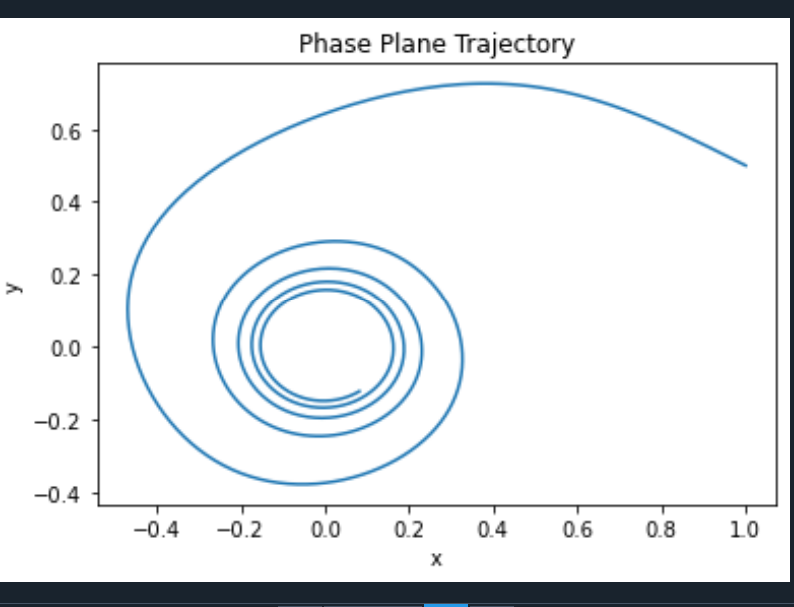
plt.figure()
plt.plot(x_solution, y_solution)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Phase Plane Trajectory')plt.show()
print("xuehao3018")

8.5:

点击查看代码

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt# 定义微分方程组
def equations(state, eta):f, df_deta, T, dT_deta = state# 用中心差分近似计算二阶导数h = 1e-4df2_deta2_approx = (state[1] - odeint(equations, [state[0]+h, df_deta+h, state[2], dT_deta], [eta])[0][1]) / h**2d2T_deta2 = -2.1 * f * dT_detareturn [df_deta, df2_deta2_approx, dT_deta, d2T_deta2]# 初始条件
f0 = 0
df_deta0 = -0.5
T0 = 1
dT_deta0 = 0
initial_conditions = [f0, df_deta0, T0, dT_deta0]# 定义 eta 的范围
eta = np.linspace(0, 10, 1000)# 求解微分方程组
solution = odeint(equations, initial_conditions, eta)
f_solution = solution[:, 0]
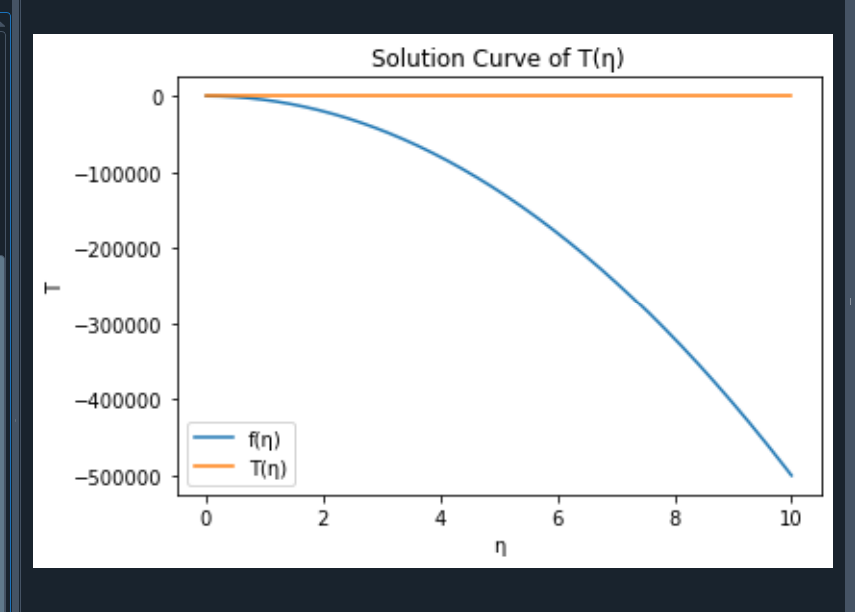
T_solution = solution[:, 2]# 绘制 f(η) 的解曲线
plt.plot(eta, f_solution, label='f(η)')
plt.xlabel('η')
plt.ylabel('f')
plt.title('Solution Curve of f(η)')# 绘制 T(η) 的解曲线
plt.plot(eta, T_solution, label='T(η)')
plt.xlabel('η')
plt.ylabel('T')
plt.title('Solution Curve of T(η)')plt.legend()
plt.show()
print("xuehao3018")