单变量微积分学习笔记：可导必连续（5）【3 ,4】

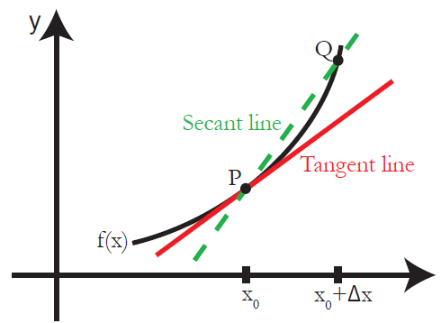
可导必连续（不连续必定不可导）

\[f'(x) = \lim_{x \to x_0} \frac{f(x) - f(x_0)}{x - x_0} \ \to \ \lim_{x \to x_0} f(x) = f(x_0) \]

\(f'(x)\lim_{x \to x_0}(x - x_0) = 0 \ \to \ \lim_{x \to x_0} \frac{f(x) - f(x_0)}{x - x_0}(x-x_0) = 0 \ \to \ \lim_{x \to x_0} f(x) - f(x_0) = 0\)