左连续和右连续
\(\lim_{x \to x_0^-} f(x) = \lim_{x \to x_0^+} f(x) = f(x_0)\)
注意:讨论是否连续的前提是函数在该点 \(x_0\) 左右邻域均有定义(不需要在 \(x_0\) 处有定义)
如我们不讨论 \(\sqrt{x}\) 在 \(0\) 处的连续性,因为 \(\sqrt{x}\) 在 \(0^-\) 没有定义
可以讨论 \(\frac{1}{x}\) 在 \(0\) 处的连续性,因为 \(\frac{1}{x}\) 在 \(0^-\) 和 \(0^+\) 均有定义,尽管在 \(0\) 处没有定义
不连续的情况
-
跳跃间断点(Jump Discontinuities)
\(\lim_{x \to x_0^-} f(x) \neq \lim_{x \to x_0^+} f(x)\)
-
可去间断点(Removable Discontinuities)
\(\lim_{x \to x_0^-} f(x) = \lim_{x \to x_0^+} f(x),f(x_0)\)不存在
-
无穷间断点(Infinite Discontinuities)
\(\lim_{x \to x_0^-} f(x) = \pm \infty \or \lim_{x \to x_0^+} f(x) = \pm \infty\)
-
震荡间断点(Other Discontinuities)
\(\lim_{x \to x_0^-} f(x) = ? \or \lim_{x \to x_0^+} f(x) = ?\)

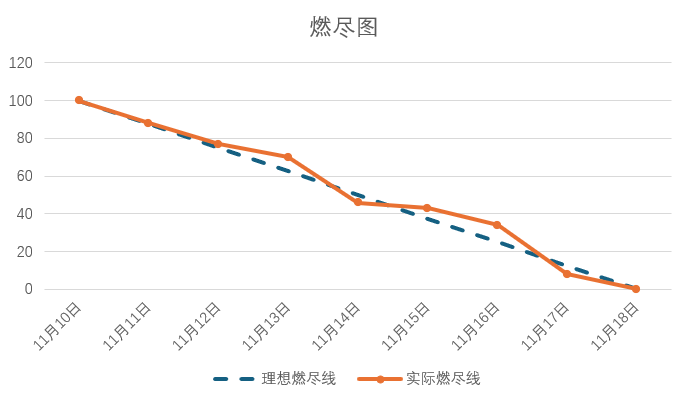
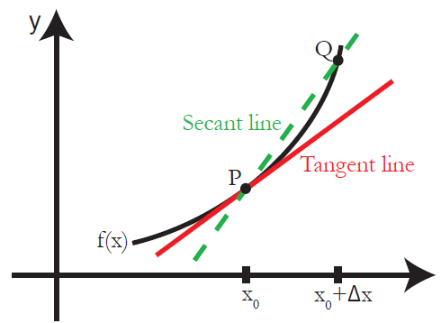

![P1314 [NOIP2011 提高组] 聪明的质监员](https://img2024.cnblogs.com/blog/3554668/202411/3554668-20241118234017795-1177984634.png)