背景
看Sutton的Reinforcement learning: An introduction,里面将策略迭代作为一种基于动态规划的方法。
书中举了个grid world的例子,非常符合书中的数学原理,有状态转移概率,每个时间步就是每个state等.....
动态规划作为一个常见的面试八股,经常出现于笔试题中,一般都是利用价值-动作表来去解决。
网上查了查,貌似目前全网所有的策略迭代的例子都是grid world这个例子,虽然很清晰,但是受限于这个问题框架,不舒服。
那么有意思的问题来了:如何使用策略迭代(Policy Iteration)解决01背包(knapsack 01)问题?
一、策略迭代
1、策略评估
给定策略\(\pi\),计算其价值函数,即为策略评估,有时也称其为预测问题。
根据贝尔曼方程:\(v_{\pi}(s) = \sum_{a}{\pi(a \mid s) \sum_{s', r}{P(s',r \mid s,a)(r + \gamma v_{\pi}(s'))}}\) 不断迭代,直至收敛,具体的伪代码算法如下:

2、策略改进
求解最优的策略和价值函数,即为策略改进,有时也称其为控制问题。
策略改进定理:如果对于任意 \(s \in S\),\(q_{\pi}(s, \pi'(s)) \geq v_{\pi}(s)\),那么策略 \(\pi'\) 不会比策略 \(\pi\) 差(一样好或者更好)。
构造一个贪心策略来满足策略改进定理:
\(
q_{\pi}(s, a) = \sum_{s', r} P(s', r \mid s, a) \left[ r + \gamma v_{\pi}(s') \right]
\)
\(
\pi'(s) = \arg\max_{a} q_{\pi}(s, a)
\)
可知通过执行这种贪心算法,我们就可以得到一个更好的策略。
3、策略迭代算法流程
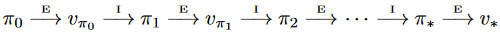

二、策略迭代代码解决01背包问题
根据我调试的经验,解决01背包问题要比解决完全背包问题更加麻烦一点。
问题在于:01背包问题中每一个物品只能拿取一次,而完全背包可以多次重复拿取。
GitHub仓库中是代码,因为顺手打开的matlab就用matlab实现了,改一下语法就是python。
https://github.com/Tylerr77/Policy-Iteration-Solving-01-Knapsack-Problem?tab=GPL-3.0-1-ov-file
% 0/1 背包问题的策略迭代
clc;
clear;
%% 输入
w = [2, 3, 4, 5, 6, 7, 8]; % 物品的重量
r = [3, 1, 5, 6, 7, 8, 9]; % 物品的价值,奖励max_W = 9; % 背包容量n = length(w); % 物品数量P = 1; % 因为选取下一个物品是固定的,所以状态转换的概率是1gama = 1; % 衰减因子% 初始化策略
policies = randi([0, n],1, max_W + 1) % 策略数组,数值表示某状态时放入物品的index,0表示不选择% 初始化价值函数
% 代表V(s),也就是V的index代表了每个状态下所能得到的最大价值,
% V(s)表示 背包容量为s - 1 状态时的价值函数(matlab索引从1开始)
V = zeros(1, max_W + 1) % 背包容量从 0 到 W,每个容量的最大价值初始化为 0% 策略迭代过程
while true% 步骤 1:策略评估% 使用当前策略计算每个状态的价值函数disp('策略评估');V_new = V; % 用于存储更新后的价值函数% 根据贝尔曼方程计算所有状态s的状态值函数% 迭代的方式进行策略评估,直到价值函数收敛while truef = 0;for s = 2:(max_W + 1)% ------------不同环境这段代码不同-------------- %% 评估当前策略下,s状态下的V(s)if policies(s) ~= 0 && w(policies(s)) <= s - 1V_new(s) = P * (r(policies(s)) + gama * V(s - w(policies(s))));elseV_new(s) = V_new(s - 1);end% --------------------------------------------- %f = max(f, abs(V_new(s) - V(s)));endif f < 1e-6break;elseV = V_new;endend% 步骤 2:策略改进% 根据当前值函数 V,选择每个状态下的最优动作disp('策略改进');policy_new = policies;policy_new(1) = 0; % s = 1背包没有空间,策略一定是不选择value_q = zeros(max_W + 1, n + 1); % q(s, a) 状态-动作对价值函数for s = 2:(max_W + 1)for a = 2:n + 1 % a = 1代表什么都不放,= 2放1号物品,= 3放2号物品....% ------------不同环境这段代码不同-------------- %% 01背包,物品仅仅可以被选中一次,但是什么都不放可以多次选中% 计算动作价值函数store = s; flag = 0;while store - w(a - 1) >= 1if policy_new(store - w(a - 1)) == a - 1flag = 1;break;endstore = store - w(a - 1);endif flag ~= 1 && w(a - 1) <= s - 1value_q(s, a) = r(a - 1) + V(s - w(a - 1));else % 什么都不放,或者放不进去,则继承上一个状态的价值,价值为value_q(s - 1)value_q(s, a) = value_q(s, a - 1);end% --------------------------------------------- %end[max_q, max_act] = max(value_q(s,:));policy_new(s) = max_act - 1;end% 如果策略没有变化,表示已经收敛if all(policy_new == policies)disp('策略已收敛');break;else% 更新策略policies = policy_new;endend% 输出最终策略和最大价值
disp('最优策略:');
disp(policies); % 输出最优策略 pi(s, a)
disp('最大价值:');
disp(V(max_W + 1)); % 输出最大价值,背包容量为 W 时的最大值
weight = max_W + 1;
while weight ~= 0 && policies(weight) ~= 0fprintf('物品 %d: 重量 = %d, 价值 = %d\n', ...policies(weight), w(policies(weight)), r(policies(weight)));weight = weight - w(policies(weight));
end