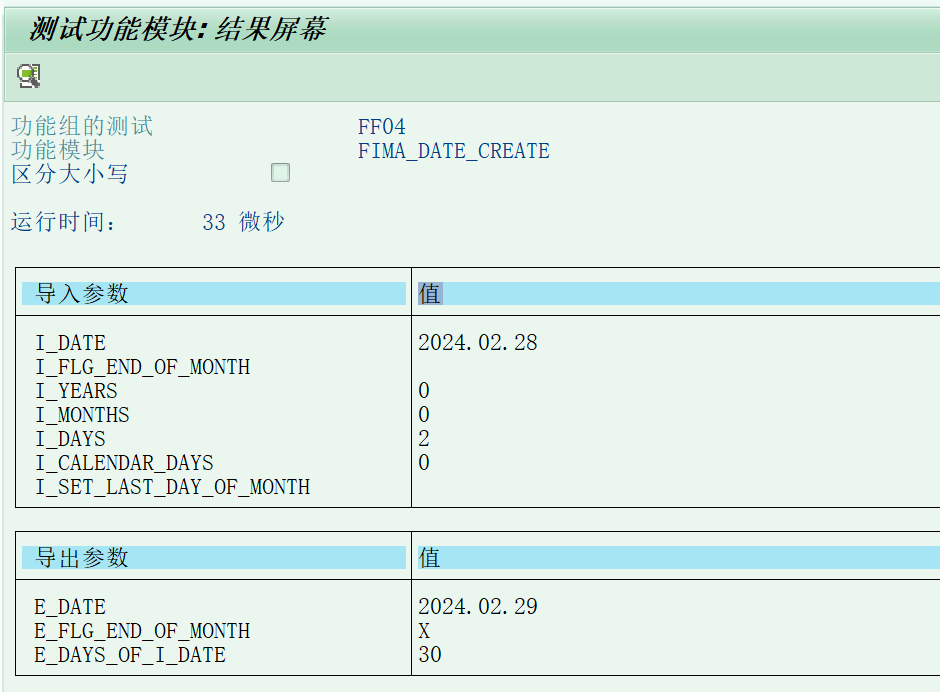
本文于 github 博客同步更新。
A:
一个数可以被操作当且仅存在一列的顶部元素为它且存在一列的底部元素为它,初始扫一遍,将合法的元素以顶部所在列为关键字扔到小根堆里,每次找到最小的元素添加,然后检查将新露出来的元素是否存在匹配,若结束时未填完即为无解。
B:
要么在非环边上砍一刀,要么在环边上砍两刀,前一种缩环的时候可以顺便计算,后一种将不再环上的点的点权加到里它最近的环上点,然后双指针维护一个小于权值和一半的区间,每次在左端点附近取几个点计算即可。
C:
考虑某一种暴力的方式,枚举最后的结果串,再判断结果串 \(s\) 是否能被 \(s_1,s_2\) 拼出,这只需要我们使用一个很简单的 dp,用\(dp[i][j]\)表示 \(s\) 考虑到第\(i\)位 ,其中 \(s_2\) 考虑到第 \(j\) 位的情况:
\(dp [i][j]=(dp[i-1][j-1] \land s[i]=s_2[j])|(dp[i-1][j] \land s[i]=s_1[i-j])\)
由上面的dp启示,我们发现 \(s_2\) 的长度非常短,可以把与 \(s_2\) 匹配位置用二进制状态压起来进行dp,用 \(f[i][now]\) 表示当前考虑到第 \(i\) 位,匹配状态为 \(now\) 的有多少种可行串,每次枚举下一个字符进行转移即可。
D:
对于权值非负和 \(tp\) 为 \(0\) 的情况,二分区间和,然后 \(n\log n\) 计算区间数量即可,时间复杂度 \(n\log n \log V\)。
 1
1