贝叶斯分类器
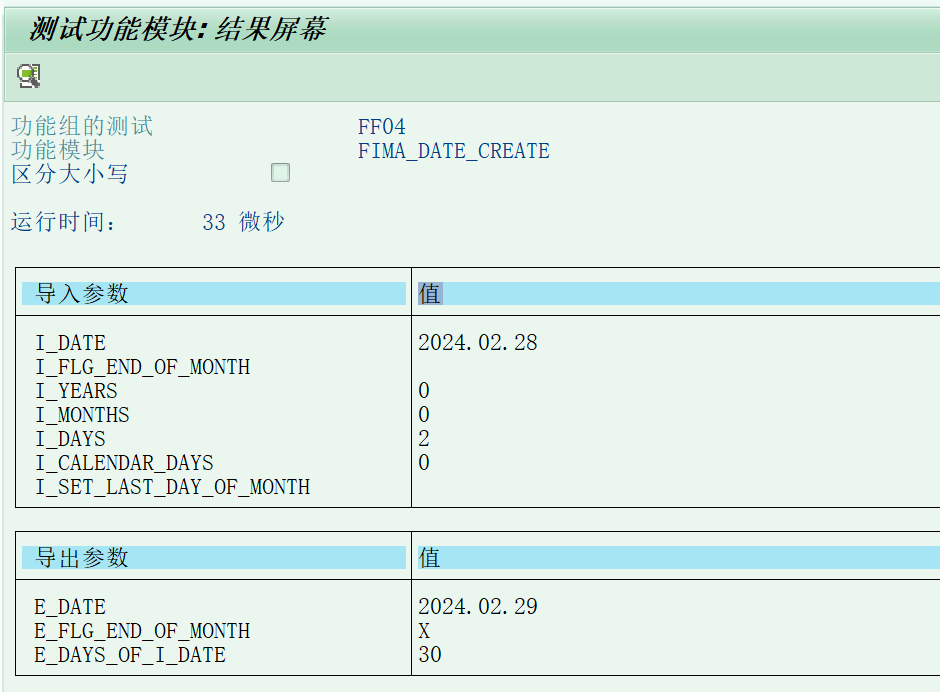
贝叶斯分类器是一类基于贝叶斯定理的统计学习方法,广泛应用于分类问题。其核心思想是通过计算后验概率 P(y∣x),将输入样本 x 分类到具有最大后验概率的类别。
1. 贝叶斯定理
贝叶斯定理是概率论中的基本法则,用于描述条件概率的关系:

其中:
- P(y∣x):在已知 x的情况下,y 属于某类的概率(后验概率);
- P(x∣y):在已知 y 属于某类的情况下,x 出现的概率(似然函数);
- P(y):y 属于某类的概率(先验概率);
- P(x):x 出现的概率(证据)。
2. 贝叶斯分类器的思想
目标
对于一个输入样本 x,分类器通过计算每个类别的后验概率 P(y∣x),选择后验概率最大的类别:
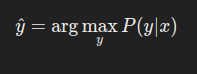
通过贝叶斯定理展开:

由于 P(x) 对所有类别相同,只需比较 P(x∣y)的大小。
贝叶斯分类器的假设
- 朴素贝叶斯分类器假设特征条件独立:

3. 贝叶斯分类器的步骤
-
计算先验概率 P(y):
- 统计每个类别在数据集中的频率。
-
计算条件概率 P(xi∣y):
- 对于每个类别 y,计算每个特征 xi 在类别 y下的条件概率。
-
计算后验概率 P(y∣x):
- 将 P(x∣y) 结合,计算后验概率。
-
分类决策:
- 选择最大后验概率的类别。
4. 示例
4.1 问题描述
假设我们有以下训练数据,目标是根据天气和风速预测是否适合运动。
| 天气 | 风速 | 是否适合运动 |
|---|---|---|
| 晴天 | 弱 | 是 |
| 晴天 | 强 | 否 |
| 多云 | 弱 | 是 |
| 雨天 | 弱 | 是 |
| 雨天 | 强 | 否 |
| 多云 | 强 | 是 |
目标是预测样本 x=(晴天,弱)是否适合运动。
4.2 步骤
(1) 计算先验概率 P(y)
- 类别“是”的样本数:4;
- 类别“否”的样本数:2;
- 总样本数:6。
P(是)=4/6=0.667,P(否)=2/6=0.333
(2) 计算条件概率 P(x∣y)
P(晴天∣是):
- 在类别“是”中,天气为“晴天”的样本有 1 个;
- 在类别“是”中总共有 4 个样本;
P(晴天∣是)=1/4=0.25
-
P(晴天∣否):
- 在类别“否”中,天气为“晴天”的样本有 1 个;
- 在类别“否”中总共有 2 个样本;
-
P(弱∣是):
- 在类别“是”中,风速为“弱”的样本有 3 个;
- 在类别“是”中总共有 4 个样本;
-
P(弱∣否):
- 在类别“否”中,风速为“弱”的样本有 0 个;
(3) 计算后验概率 P(y∣x)
对于类别“是”:
P(是∣晴天,弱)∝P(晴天∣是)⋅P(弱∣是)⋅P(是)
P(是∣晴天,弱)∝0.25⋅0.75⋅0.667=0.125
对于类别“否”:
P(否∣晴天,弱)∝P(晴天∣否)⋅P(弱∣否)⋅P(否)
P(否∣晴天,弱)∝0.5⋅0⋅0.333=0
(4) 分类决策
P(是∣晴天,弱)=0.125>P(否∣晴天,弱)=0
因此,样本 x=(晴天,弱)的预测结果是“是”。
The symbol "∝" represents proportionality in mathematics. When you see a∝b, it means that a is proportional to bbb, or a=k⋅ba = k \cdot ba=k⋅b, where kkk is a constant of proportionality.
For example:
- If F∝x, then F=kx for some constant kkk.
- Proportionality often indicates that as one variable changes, the other changes in a consistent way (e.g., doubling b will double a if a∝ba ).
5. 优缺点
优点
- 简单高效:计算简单,适合大规模数据。
- 易于解释:基于概率,结果直观。
- 适合离散数据:对于类别型特征表现良好。
缺点
- 条件独立性假设:假设特征条件独立,在实际问题中可能不成立。
- 零概率问题:如果某个条件概率为零,会导致整体概率为零(可通过平滑解决)。
- 对连续特征不够友好:需要额外处理(如用高斯分布拟合)。
6. 常见应用
- 文本分类(如垃圾邮件过滤)。
- 医学诊断。
- 客户分类和信用风险评估。
贝叶斯分类器以其简洁高效的特点,成为机器学习中的重要基础方法之一,特别是在特征独立性假设近似成立的场景中表现突出。