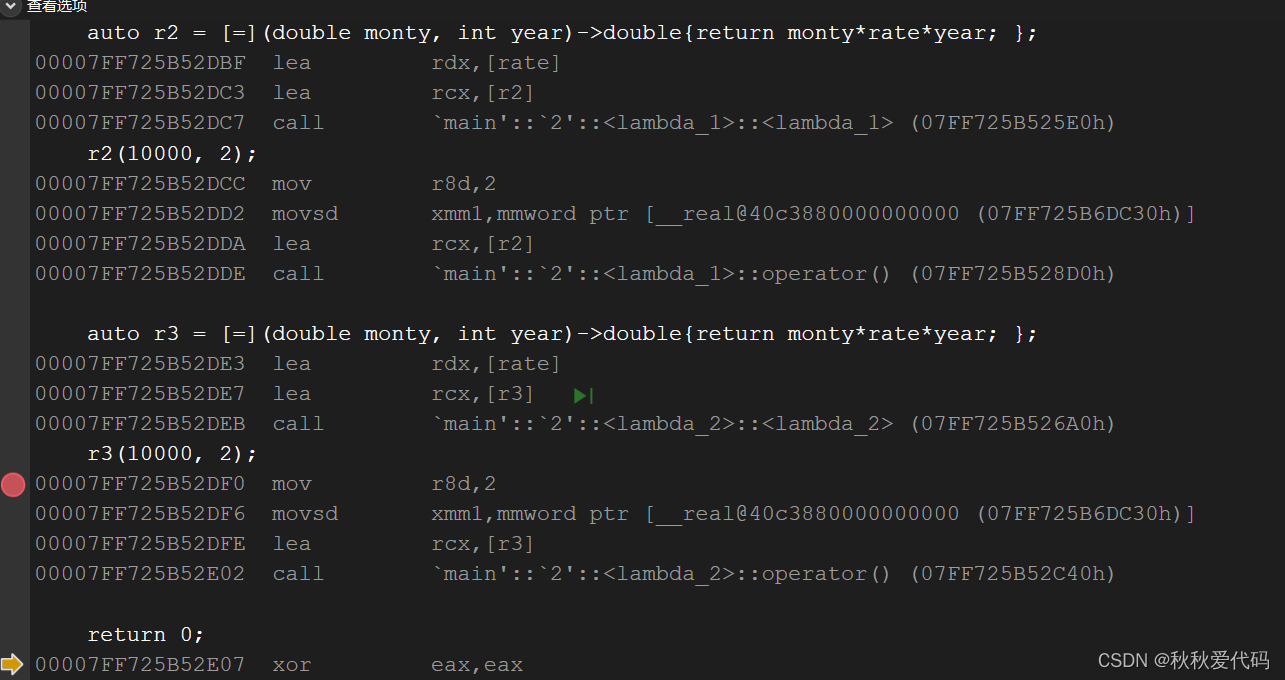
二叉树
一棵二叉树是结点的一个有限集合,该集合或者为空,或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
二叉树的特点:
- 每个结点最多有两棵子树,即二叉树不存在度大于2的结点。
- 二叉树的子树有左右之分,其子树的次序不能颠倒。
满二叉树
满二叉树:二叉树的所有叶子节点都在最后一层且总数n=2^(n-1)。

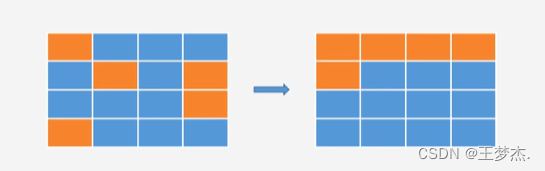
完全二叉树
完全二叉树:数据从上到下,从左到右依次进行平铺。
有序二叉树
有序二叉树:左子树上的值小于根节点的值,右子树上的值大于根节点的值。
有序二叉树的遍历:
深度优先遍历:
1、先序/前序遍历:根节点----》左子树-----》右子树
2、中序遍历:左子树----》根节点-----》右子树
3、后序遍历:左子树----》右子树-----》根节点
有序二叉树不稳定:O(logn) - O(n)
有序二叉树不稳定是因为没有任何限制,以至于在某些特殊的情况下会形成链表。
平衡二叉树
平衡二叉树是在有序二叉树的基础之上而来的,就是为了解决有序二叉树不稳定的问题。要求:一个节点的左右子树高度差的绝对值不能超过1,可以等于1。
如果插入的数据之后使得一个节点的左右子树高度差的绝对值超过了1,就要通过LL、RR、LR、RL四种旋转策略来保证平衡二叉树。
四种旋转策略
LL旋转策略:

实例:

RR旋转策略:

实例:

LR旋转策略:

实例:

RL旋转策略:

实例:
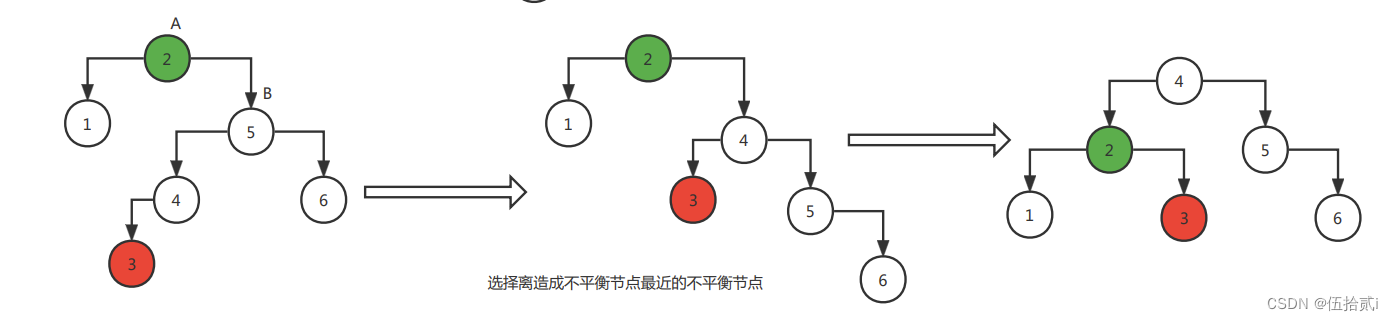
在实行旋转策略是,选择距离造成不平衡节点最近的不平衡节点作为要操作节点。
平衡二叉树特别稳定,但每次进行调整都会耗费计算机性能。
我们想既要时间复杂度在O(logn),又要十分稳定,还要不耗费计算机性能,这时,推出了红黑树。
红黑树(基于2-3-4树)
2-3-4树是从下向上构建的。节点内升序,每个节点最多有3个值,当插入第4个值时,需要在这四个之中选中间值进行升元。
实例:

然后通过2-3-4树转换 形成红黑树
转换规则如下图:

将刚刚的2-3-4树转换为红黑树:

红黑树的特点:
1、红黑树中每一个节点不是红色节点就是黑色节点。
2、红黑树当中根节点一定是黑色的。———>在转化的过程中2-3-4节点都是以黑色节点开头的
3、每一个叶子节点都是黑色的。
4、从根节点到任意一个叶子节点的路径上所走过的黑色节点的数量相同
5、如果一个节点是红色的,那么他的子节点一定是黑色
4、5条特点会导致最长的路径绝对不会超过最短路径的2倍。例如最长路径为黑红黑红黑红,最短路径为黑黑黑。
为什么红黑树是O(logn)?
2-3-4树是多叉树,如果数据相等,它的时间复杂度小于传统二叉树,2-3-4树的时间复杂度
红黑树最复杂的时候也就是变为2倍,变为2logn。这是依旧可以看成是logn。
B树
多叉树以B树为最基本点。2-3-4树来源于B树。
B树特点:
1、B树的数据存储是 key-value类型的。
2、B树有几个叉:并不确定,要看具体实现。
3、M阶B树
3.1、每个节点上最多有 M-1 个值,并且以升序排列。3阶B树每个节点最多有两个值。.....(2-3-4树属于4阶B树)
红黑树和B树如果都在内存中,内存向cpu提供数据的时间相等,由于红黑树对比次数相对较少,所以红黑树是内存最优二叉树。
为什么要有B树:
红黑树和B树如果都在磁盘中--------》数据寻址浪费时间--------》磁头移动的物理时间+平均盘面旋转半圈
B树多用于磁盘,原因是分出多个叉,降低树的高度,降低寻址次数和时间。
B树优胜于寻址,但是数据进行对比还是要在内存中。
B+树
在B树基础上改造出现的B+树,但和传统B树又不太一样。B+树是mysql数据库专用底层数据结构。
B+树的特点:
1、非叶子节点仅具有索引功能,也就是说非叶子节点只能存储key值,不能存储value值。
2、B+树的所有叶子节点会构成一个有序的链表,这样就可以根据key值遍历数据。
之所以有这两个特点就是为数据库的功能服务
B+树的构建

插入 3 ,4

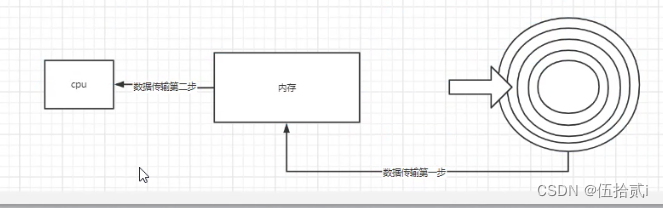
磁盘向cpu推送数据:每次需要推送一页(4kb)的数据,如两个文件 2kb+3kb,只能先推送2kb,再推送3kb。
B+树的优点:
1、非叶子节点不包含数据,只能放索引,这样每次就可以向内存当中传输更多的key值,在内存当中进行数据比对,在磁盘当中进行数据查询。
2、叶子节点是链接在一起的,这样有利于区间查询。