【MX-S7】梦熊 NOIP 2024 模拟赛 3 SMOI Round 2

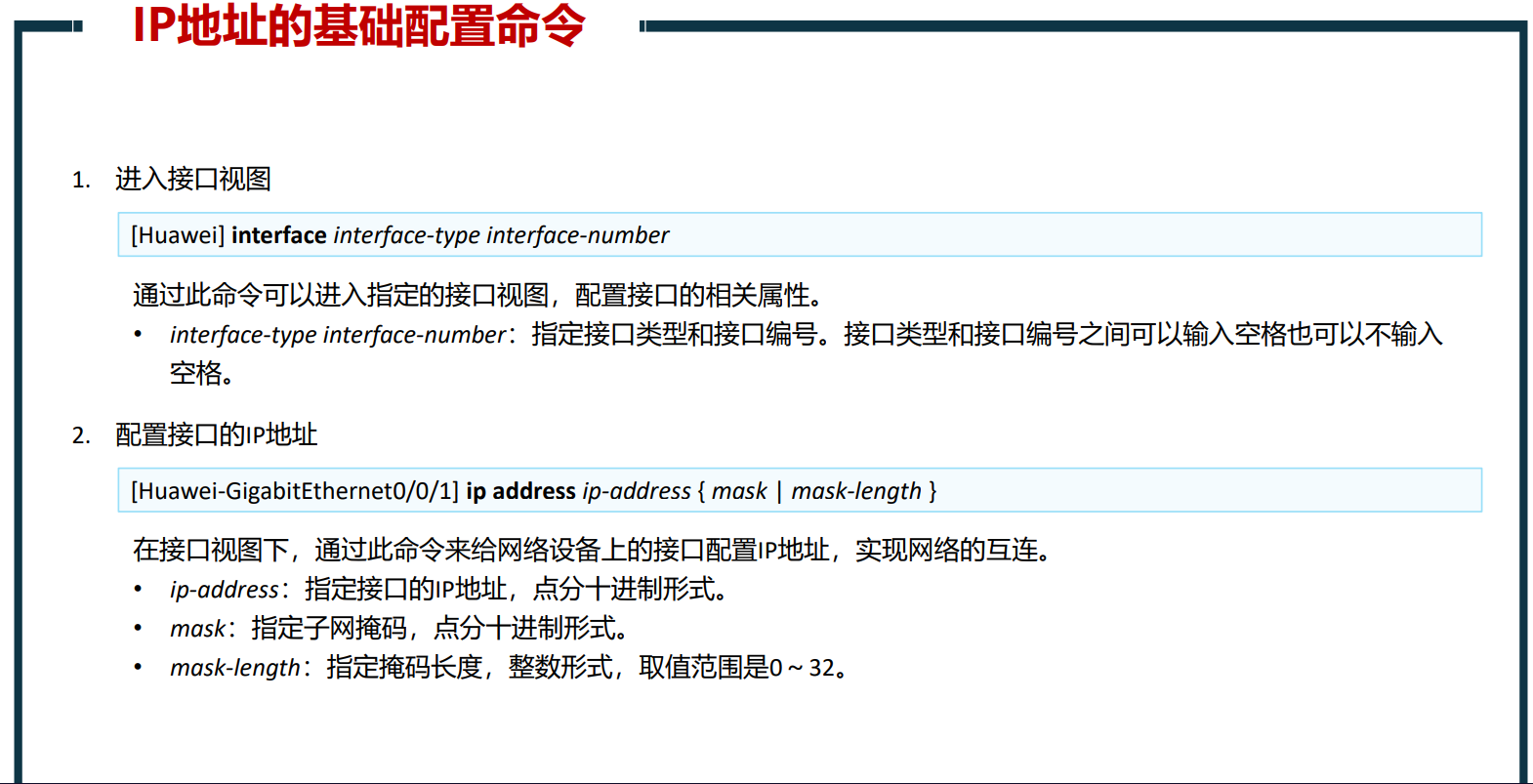
俩签到俩不可做是吧。

Rank

【MX-S7-T1】「SMOI-R2」Happy Card

签到题一号，以为撑死评个黄但没想到那么多人不会打扑克。

考虑炸弹也是三带一，出三带一肯定更优秀。

考虑将所有牌变为若干个三张和剩余的，那么三张先带单张，再将对子拆开带。那么现在就有以下几种情况：

1. 单张太多，那么就是将所有三带用完然后出对子和单张。
2. 三张有剩余，再根据对子的数量分情况：
   1. 对子将三张耗完了，那么剩下的就当对子出，注意特判是否剩一张凑不成对子。
   2. 三张有剩余，考虑三张之间自行消耗，具体的，将一个三张分成三个单张，然后带走其他三个三张即可。考虑剩余：如果剩余一个三张，那么将这个分成一个对子和一张单牌；余两个，那么将这个分成一个三带一和一个对子；余三个，分成两个三带一和一张单牌。
      依照上文模拟即可，时间复杂度\(O(n)\)。

点此查看代码

#include<bits/stdc++.h>
using namespace std;
#define rep(i,s,t,p) for(int i = s;i <= t; i += p)
#define drep(i,s,t,p) for(int i = s;i >= t; i -= p)
#ifdef LOCALFILE *InFile = freopen("file/in.in","r",stdin),*OutFile = freopen("file/out.out","w",stdout);
#elseFILE *InFile = stdin,*OutFile = stdout;// FILE *InFile = freopen("card.in","r",stdin),*OutFile = freopen("card.out","w",stdout);
#endif
using ll=long long;using ull=unsigned long long;
using db = double;using ldb = long double;
#define int long long
const int N = 3e5 + 10;
int n,a[N],ct[3];
inline void solve(){cin>>n;rep(i,1,n,1) cin>>a[i];ll ans = 0,ct3 = 0;memset(ct,0,sizeof ct);rep(i,1,n,1) ct3 += a[i]/3,ct[a[i]%3]++;int res = min(ct3,ct[1]);ans += res,ct3 -= res;ct[1] -= res;if(!ct3) cout<<ans + ct[2] + ct[1]<<'\n';else{if(ct[2]*2 >= ct3){ans += ct3;if(ct3&1){ans += (2*ct[2]-ct3)/2+1;}else ans += (2*ct[2] - ct3)/2;}else{ans += ct[2]*2;ct3 -= ct[2]*2;ans += ct3/4*3;ct3 %= 4;if(ct3 == 1) ans += 2;if(ct3 == 2) ans += 2;if(ct3 == 3) ans += 3;}cout<<ans<<'\n';}
}
signed main(){cin.tie(nullptr)->sync_with_stdio(false);int T;cin>>T;while(T--) solve();
}

【MX-S7-T2】「SMOI-R2」Speaker

半个签，但是不懂为啥只评了个绿。

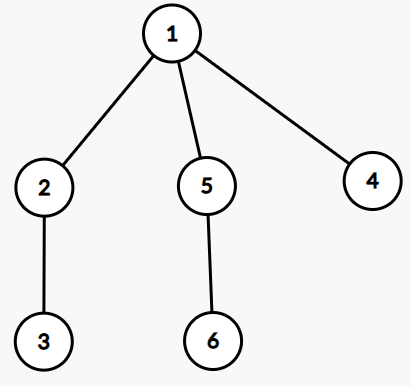
记 \(f_x\) 表示 \(x\) 子树内所有的点到 \(x\) 的最大贡献（贡献定义为 \(c_i-\text{路径长度}\)，下同）。显然有 \(f_x=\max\limits_{y\in son_x}f_y-2\times dist(x,y)\)。

记 \(g_x\) 表示 \(x\) 子树外所有的点到 \(x\) 的最大贡献，显然有 \(g_x=\max\{f_{fa_x},g_{fa_x}\}-2\times dist(fa_x,x)\)。

然后额外的贡献就是 \(x\to y\) 路径上 \(f\) 的最大值和 \(g_{LCA(x,y)}\) 取 \(\max\)。

写个树剖+ST表或者倍增写一下即可，时间复杂度 \(O(n+q\log n)\) 或 \(O(n\log n+q\log n)\)。

点此查看代码

#include<bits/stdc++.h>
using namespace std;
#define rep(i,s,t,p) for(int i = s;i <= t; i += p)
#define drep(i,s,t,p) for(int i = s;i >= t; i -= p)
#ifdef LOCALFILE *InFile = freopen("file/in.in","r",stdin),*OutFile = freopen("file/out.out","w",stdout);
#elseFILE *InFile = stdin,*OutFile = stdout;
#endif
using ll=long long;using ull=unsigned long long;
using db = double;using ldb = long double;
#define int long long
#define eb emplace_back
const int N = 2e5 + 10;
struct node{int to,w;node(int T,int W):to(T),w(W){};};vector<node>e[N];
int n,q;
int top[N],siz[N],son[N],dfn[N],rdfn[N],tim,fa[N],dep[N],f[N],a[N],g[N],dist[N];
int st[19][N],lg[N];
inline void pre(){rep(i,2,n,1) lg[i] = lg[i >> 1] + 1;rep(i,1,n,1) st[0][i] = f[rdfn[i]];int t = lg[n];rep(j,1,t,1) rep(i,1,n-(1<<j)+1,1) st[j][i] = max(st[j-1][i],st[j-1][i+(1<<(j-1))]);
}
inline int qry(int l,int r){int k = lg[r-l+1];return max(st[k][l],st[k][r-(1<<k)+1]);}
void dfsf(int x,int fa){f[x] = a[x];for(auto [y,w]:e[x]){if(y == fa) continue;dfsf(y,x);f[x] = max(f[x],f[y] - 2*w);}
}
void dfsg(int x,int fa){for(auto [y,w]:e[x]){if(y == fa) continue;g[y] = max(g[x],f[x]) - 2*w;dfsg(y,x);}
}
void dfs1(int x){siz[x] = 1;dep[x] = dep[fa[x]] + 1;for(auto [y,w]:e[x]){if(y == fa[x]) continue;fa[y] = x;dist[y] = dist[x] + w;dfs1(y);siz[x] += siz[y];if(siz[son[x]] < siz[y]) son[x] = y;}
}
void dfs2(int x,int t){top[x] = t;rdfn[dfn[x] = ++tim] = x;if(son[x]) dfs2(son[x],t);else return;for(auto [y,w]:e[x]){if(y == fa[x] || y == son[x]) continue;dfs2(y,y);}
}
inline int query(int x,int y){int res = a[x] + a[y] - dist[x] - dist[y],fx = top[x],fy = top[y],add = max(f[x],f[y]);while(fx ^ fy){if(dep[fx] < dep[fy]) swap(x,y),swap(fx,fy);add = max(add,qry(dfn[fx],dfn[x]));x = fa[fx],fx = top[x];}if(dep[x] > dep[y]) swap(x,y);add = max(add,qry(dfn[x],dfn[y]));add = max(g[x],add);res += dist[x]*2;return res + add;
}
inline void solve(){cin>>n>>q;rep(i,1,n,1) cin>>a[i];rep(i,2,n,1){int u,v,w;cin>>u>>v>>w;e[u].eb(v,w);e[v].eb(u,w);}memset(f,-0x3f,sizeof f);memset(g,-0x3f,sizeof g);dfsf(1,0);dfsg(1,0);dfs1(1);dfs2(1,1);pre();rep(test,1,q,1){int x,y;cin>>x>>y;cout<<query(x,y)<<'\n';}
}
signed main(){cin.tie(nullptr)->sync_with_stdio(false);solve();
}

【MX-S7-T3】「SMOI-R2」Monotonic Queue

没看懂题，就会依照题意模拟了。

令\(a_{n+1}=inf\)，记\(R_i\)为\(a\)中\(i\)右边第一个大于\(a_i\)的数的位置。如果一个数\(c_i\)有贡献，当且仅当存在一个\(j\)满足\(l_j\le R_i\And R_i\le r_{i+1}\)，这个可以通过手膜出来。发现如果存在\(i\)满足\(l_i=l_{i+1}\)，那么区间\([l_{i+1},r_{i+1}]\)是无用的，因为有贡献的还是有贡献，没贡献的还是没贡献。所以就钦定\(l_i=i\)即可。

那么此时\(c_i\)有贡献的条件变成了\(R_i\le r_{j+1}\)，假设\(r^\prime_i=r_{i+1}\)，那么\(r^\prime_i\)可以取到时当且仅当\(i+1\le r^\prime_i\le n,r^\prime_i\le r^\prime_{i+1}\)。

设\(f_{i,j}\)表示考虑了\(r^\prime_{1\cdots i}\)的取值，且\(r^\prime_i=j\)时的最优答案，那么\(f_{i,j}=[j\le R_i]\max\limits_{k=i}^jf_{i-1,k}\)。答案为\(\max\limits_{i=1}^{n-1}f_{i,i+1}\)。

考虑这个东西就是求前缀\(\max\)和区间加法，考虑线段树维护，每次更新相当于\([R_i,n]\)加\(c_i\)，但是如果\(c_i<0\)，那么就要重新维护一下单调性，具体的，线段树上二分求出第一个\(\ge f_{i,R_i-1}\)的位置\(p\)，将\([R_i,p]\)区间覆盖成\(f_{i,R_i-1}\)，时间复杂度\(O(n\log n)\)。

点此查看代码

#include<bits/stdc++.h>
using namespace std;
#define rep(i,s,t,p) for(int i = s;i <= t; i += p)
#define drep(i,s,t,p) for(int i = s;i >= t; i -= p)
#ifdef LOCALFILE *InFile = freopen("file/in.in","r",stdin),*OutFile = freopen("file/out.out","w",stdout);
#elseFILE *InFile = stdin,*OutFile = stdout;
#endif
using ll=long long;using ull=unsigned long long;
using db = double;using ldb = long double;
#define int long long
const int N = 5e5 + 10;
const ll inf = 0x3f3f3f3f3f3f3f3f;
int n,a[N],c[N],r[N];stack<int> sta;
struct Segment_Tree{struct segment_tree{int l,r;ll val,lz,cover;#define l(x) tree[x].l#define r(x) tree[x].r#define val(x) tree[x].val#define lz(x) tree[x].lz#define cover(x) tree[x].cover}tree[N<<2];inline void P(int k){val(k) = max(val(k<<1),val(k<<1|1));}inline void D(int k){int ls = k<<1,rs = k<<1|1;if(cover(k) != inf){val(ls) = cover(k);val(rs) = cover(k);lz(ls) = lz(rs) = 0;cover(ls) = cover(rs) = cover(k);cover(k) = inf;}if(lz(k)){val(ls) += lz(k);val(rs) += lz(k);lz(ls) += lz(k);lz(rs) += lz(k);lz(k) = 0;}}void B(int k = 1,int l = 1,int r = n){l(k) = l,r(k) = r,lz(k) = 0,cover(k) = inf;if(l == r) return val(k) = 0,void();int mid = (l + r) >> 1;B(k<<1,l,mid);B(k<<1|1,mid+1,r);P(k);}void U1(int k,int l,int r,int val){if(l <= l(k) && r(k) <= r) return val(k) += val,lz(k) += val,void();D(k);int mid = (l(k) + r(k)) >> 1;if(l <= mid) U1(k<<1,l,r,val);if(r > mid) U1(k<<1|1,l,r,val);P(k);}void U2(int k,int l,int r,int val){if(l <= l(k) && r(k) <= r) return val(k) = val,lz(k) = 0,cover(k) = val,void();D(k);int mid = (l(k) + r(k)) >> 1;if(l <= mid) U2(k<<1,l,r,val);if(r > mid) U2(k<<1|1,l,r,val);P(k);}int qry1(int k,int p){if(l(k) == r(k)) return val(k);D(k);return (p <= ((l(k) + r(k))>>1))?qry1(k<<1,p):qry1(k<<1|1,p);}int qry2(int k,int l,int r,int p){if(val(k) < p) return -1;if(l(k) == r(k)) return l(k);D(k);int mid = (l(k) + r(k)) >> 1;if(r <= mid) return qry2(k<<1,l,r,p);if(l > mid) return qry2(k<<1|1,l,r,p);int res = qry2(k<<1,l,r,p);if(res == -1) return qry2(k<<1|1,l,r,p);return res;}#undef l#undef r#undef val#undef lz#undef cover
}T;
inline void solve(){cin>>n;rep(i,1,n,1) cin>>c[i];rep(i,1,n,1) cin>>a[i];a[n + 1] = 1e9+10;rep(i,1,n + 1,1){while(sta.size() && a[sta.top()] < a[i]) r[sta.top()] = i,sta.pop();sta.emplace(i);}T.B();ll ans = 0;rep(i,1,n-1,1){T.U2(1,i,i,-inf);if(r[i] > n) continue;T.U1(1,r[i],n,c[i]);if(c[i] < 0){int lst = T.qry1(1,r[i]-1),pos = T.qry2(1,r[i],n,lst);if(pos == -1) T.U2(1,r[i],n,lst);else if(pos - 1 >= r[i]) T.U2(1,r[i],pos-1,lst);}ans = max(ans,T.qry1(1,i+1));} cout<<ans<<'\n';
}
signed main(){cin.tie(nullptr)->sync_with_stdio(false);solve();
}

MX-S7-T4】「SMOI-R2」XA-Game

不会

p