大模型--模型量化GPTQ--23-编程知识

大模型--模型量化GPTQ--23

news/2024/11/27 9:42:35/文章来源:https://www.cnblogs.com/cavalier-chen/p/18571604

1. 参考
2. OBD
3. OBS
4. 从 OBS 到 OBQ
5. GPTQ Gradient PreTrained Quantity

1. 参考

GPTQ 量化技术演进：https://zhuanlan.zhihu.com/p/690834228?utm_id=0
OBS/OBD/GPTQ：https://www.cnblogs.com/wangbingbing/p/17547681.html

GPTQ使用的方法改进自OBC(Frantar, 2022)，OBC来源于OBS(Hassibi, 1992)，OBS来源于OBD(Lecun, 1990)

2. OBD

OBD 的基本思想是以模型训练损失为目标函数，迭代地选择剪枝参数使目标函数Loss最小化。
设模型的权重为w，损失函数为f，则在当前权重下，模型的训练损失为。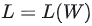
对损失函数进行泰勒展开可以估计权重调整造成的影响，对进行泰勒展开：

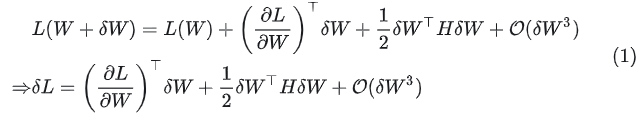
其中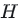：是 Hessian 矩阵
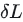是剪枝后损失的变化量，显然越小越好
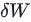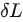目标就是找到一个，使得最小。

一个训练好的神经网络模型，其损失一般都处于权重空间中的局部极小值，因此可以认为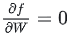，因此式中的第一项可以忽略。另外再忽略高阶项，则上式可以简化为：

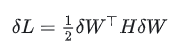
介绍 OBD 的一个重要假设，为了进一步简化问题，OBD 认为 Hessian 矩阵是一个对角矩阵--也就是只有对角线有元素，其他全为0，其含义是，同时剪枝多个权重参数对模型精度造成的影响，等于单独剪枝每个权重对模型造成影响之和

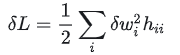
最终需要求解的问题就成了

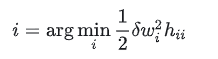
3. OBS

OBS 受到 OBD 关于减小模型剪枝对损失函数影响的启发，但是不同意 OBD 的假设。
认为权重剪枝之间是有关联的，所以不能简单地将 Hessian 矩阵假设为对角矩阵

再次分析：

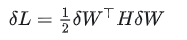
假设对第q个参数进行剪枝，

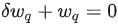
也就是对应位置的权重置为0，

于是这里就变成了带约束的凸优化问题：

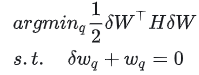
其中：约束条件可以写成更一般的形式：

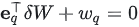
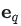第q个值为 1 的单位向量。

对于上述问题，可以使用拉格朗日乘子法来求解，定义拉格朗日函数：

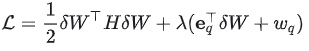
对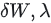求导，并设置为 0

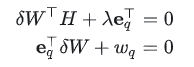
然后做如下变换：

对一个方程乘以
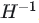
交换第二个方程的，：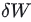

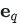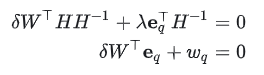
第二个方程乘以
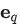
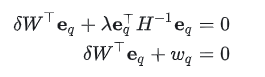
注意到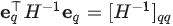并将第二个方程带入第一个方程
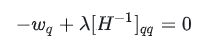
得到
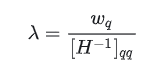
第一个方程，解得

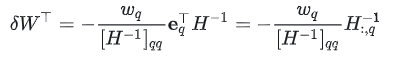
其中：
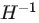表示的第q列，

获得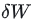之后带入损失函数

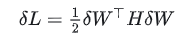
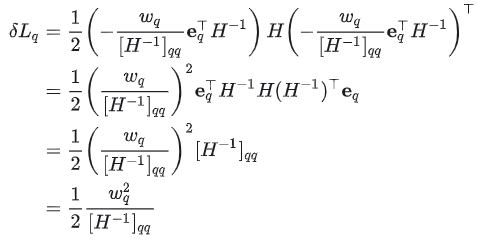
得到：

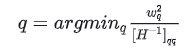
可以找到当前最优的剪枝参数q，再使用公式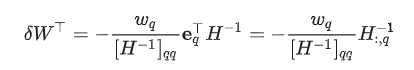计算所有权重的修正量，这就完成了一次迭代。不断找到需要剪枝的权重参数，直到达到剪枝的目标。

4. 从 OBS 到 OBQ

剪枝和量化都涉及到对权重值的修改，只不过剪枝是直接将权重设置为 0，而量化则是降低权重值的数值精度，比如将 fp32 数值变成 fp16，int8，int4 等
OBS 的思想可以很自然的应用到量化上来，这种方法也被称为OBQ (Optimal Brain Quantization)，为了兼顾剪枝和量化，论文的标题就叫 OBC (Optimal Brain Compression)。

从这个公式出发：

在 OBS 中，对应的约束条件为，
索引为 q 的权重修改量为，