1 引入原因
- K近邻算法需要在整个数据集中搜索和测试数据x最近的k个点,如果一一计算,然后再排序,开销过大
- 引入KD树的作用就是对KNN搜索和排序的耗时进行改进
2 KD树
2.1 主体思路
- 以空间换时间,利用训练样本集中的样本点,沿各维度依次对k维空间进行划分,建立二叉树
- 利用分治思想提高算法搜索效率
- 二分查找的算法复杂度是O(logN)
,KD树的搜索效率与之接近(取决于所构造kd-tree是否接近平衡树)
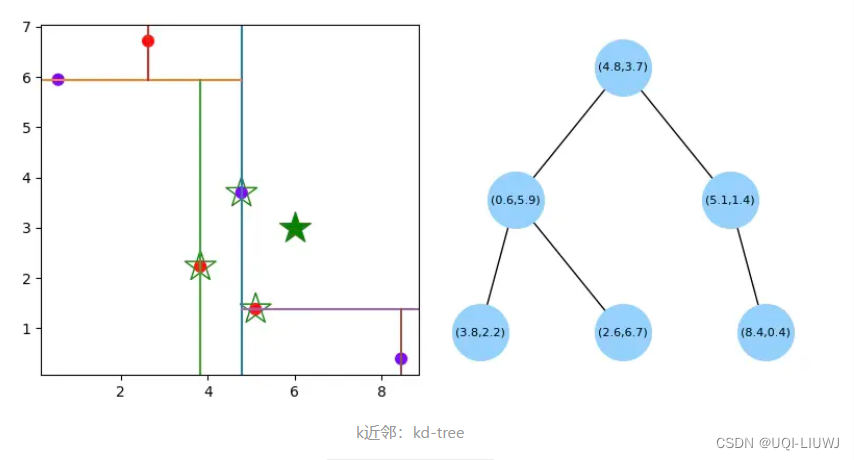
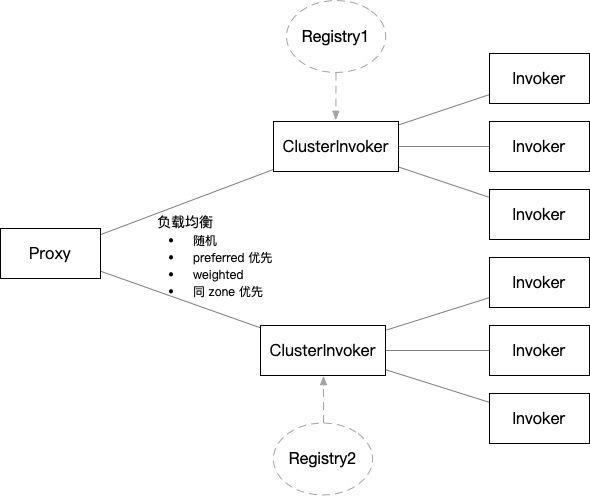
- 上图为为训练样本对空间的划分以及对应的kd树
- 绿色实心五角星为测试样本,通过kd-tree的搜索算法,快速找到与其最近邻的3个训练样本点(空心五角星标注的点)
2.2 KD树的建立
2.2.1 以一个例子引入
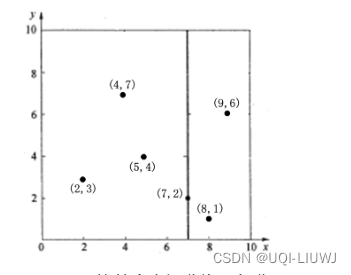
- 比如我有6个点:(2,3),(4,7),(5,4),(7,2),(8,1),(9,6)
- 1) 数据有两个维度,分别计算x,y方向上数据的方差
- x方向上的方差最大
- ——>先沿着X轴方向进行split
- 注:这一步也可以不要,因为KD树适用的问题大多是维度小于20的,所以按照维度顺序一个一个来也没有问题
- 2)根据x轴方向的值2,5,9,4,8,7排序选出中位数为7
- x≤7的和x >7的被分开了
- x≤7的和x >7的被分开了
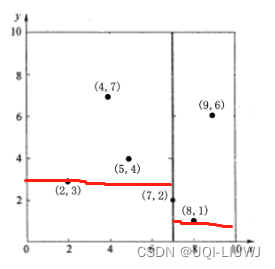
- 3) 被分开的左半区和右半区分别选出y轴方向的中位数(偶数选小的那个)
- 4)左上方三个点再根据x轴分一刀(其他三个区域已经各只剩一个点了)
- 最终得到的KD树
2.2.2 伪代码
def kd_tree_construct:input: x: 训练样本集dim: 当前节点的分割维度(子节点的分割维度=(dim+1)%样本的维度)output: node: 构造好的kd tree的根节点if 只有一个数据点:创建一个叶子结点node包含这一单一的点node.point = x[0]node.son1 = Nonenode.son2 = Nonereturn nodeelse:记dim维度上的中位点为x(对x中的数据按dim维排序,取中位点,偶数个则取较小的那个)记xl为左集合(dim维小于p点的所有点)记xr为右集合(dim维大于p点的所有点)创建带有两个孩子的node:node.point = pnode.son1 = fit_kd_tree(xl)node.son2 = fit_kd_tree(xr)return node2.3 KD树上的最近邻查找
2.3.1 伪代码
def kd_tree_search:global:Q, 缓存k个最近邻点(初始时包含一个无穷远点)q, 与Q对应,保存Q中各点与测试点的距离input: k, 寻找k个最近邻t, 测试点node, 当前节点(一开始时根节点)dim, 当前节点的分割维度(子节点的分割维度=(dim+1)%数据点的维度)output: 无if distance(t, node.point) < max(q):将node.point添加到Q,并同步更新q若Q内超过k个近邻点,则移出与测试点距离最远的那个点,并同步更新qif t[dim]-max(q) < node.point[dim]:kd_tree_search(k,t,node.son1)if t[dim]+max(q) > node.point[dim]:kd_tree_search(k,t,node.son2)
2.3.1 以一个例子开始
2.3.1.1 例子1
搜索(2.1,3.1)
记k=1
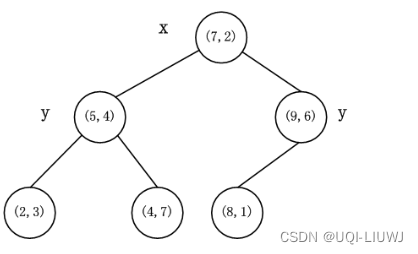
- 第1步:将(7,2)加入Q中,maxq=5.02,更新Q
- 2.1-5.02≤7
- 搜索左儿子
- 第2步:将(5.4)加入Q中,maxq=3.04,更新Q
- 3.1-3.04≤4
- 搜索下儿子
- 第3步:将(2,3)加入Q中,maxq=0.1414,更新Q
- 已经是叶子节点了,结束
- 3.1-3.04≥4
- 搜索上儿子
- 第4步:将(4,7)加入Q中,maxq=4.338>0.1414,不更新Q,仍为0.1414
- 已经是叶子节点了,结束
- 3.1-3.04≤4
- 2.1-5.02≥7
- 搜索右儿子
- 第5步,将(9,6)加入Q中,maxq=7.484>0.1414,不更新Q,仍为0.1414
- 3.1+7.484>6
- 搜索上儿子
- 没有上儿子,结束
- 2.1-5.02≤7
- 算法结束,最近的点是(2,3),q=0.1414
2.3.1.2 例子2 回溯时改变最近邻点
假设我们要查询的点是2,4.5
同样记k=1

- 第1步:将(7,2)加入Q中,maxq=5.59,更新Q
- 2-5.59≤7
- 搜索左儿子
- 第2步:将(5.4)加入Q中,maxq=3.04,更新Q
- 4.5-3.04≤4
- 搜索下儿子
- 第3步:将(2,3)加入Q中,maxq=1.5,更新Q
- 4.5+3.04≥4
- 搜索上儿子
- 第4步:将(4,7)加入Q中,maxq=3.20>1.5,不更新Q,仍为1.5
- 4.5-3.04≤4
- 2+5.59 >7
- 搜索右儿子
- 第5步,将(9,6)加入Q中,maxq=7.16>1.5,不更新Q,仍为1.5
- 4.5+7.16>6
- 搜索上儿子
- 没有上儿子,结束
- 4.5+7.16>6
- 2-5.59≤7
- 算法结束,最近的点是(2,3),距离为1.5
参考内容:KNN的核心算法kd-tree和ball-tree - 简书 (jianshu.com)
k-d tree算法 - J_Outsider - 博客园 (cnblogs.com)

![[C#][原创]操作注册表一些注意点](https://img-blog.csdnimg.cn/img_convert/a27162d9b3fbbcd63bf659c7d9645a5f.gif)




![java八股文面试[Spring]——如何实现一个IOC容器](https://img-blog.csdnimg.cn/img_convert/f021207ca7c074ef3cc030ca5c3691f9.png)


![[matlab]matlab配置mingw64编译器](https://img-blog.csdnimg.cn/670dca82206f4d4e9a3ce799b27ab248.png)