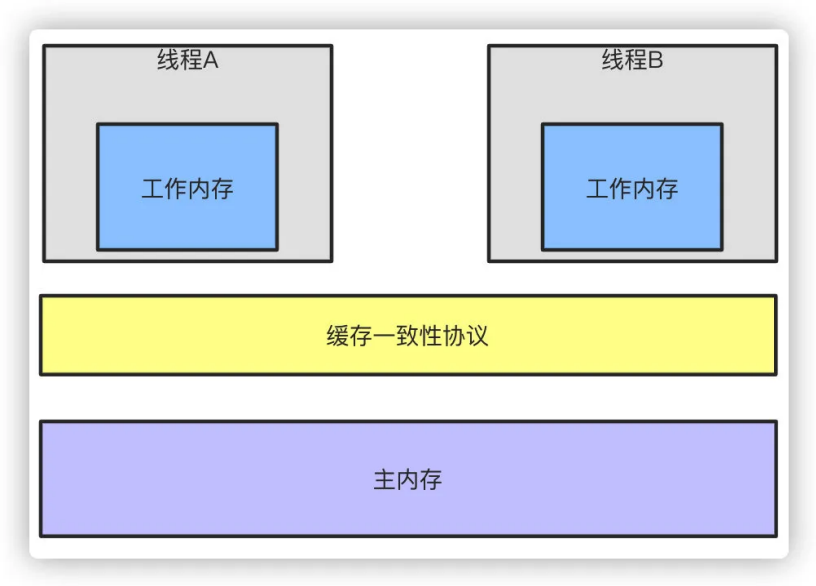
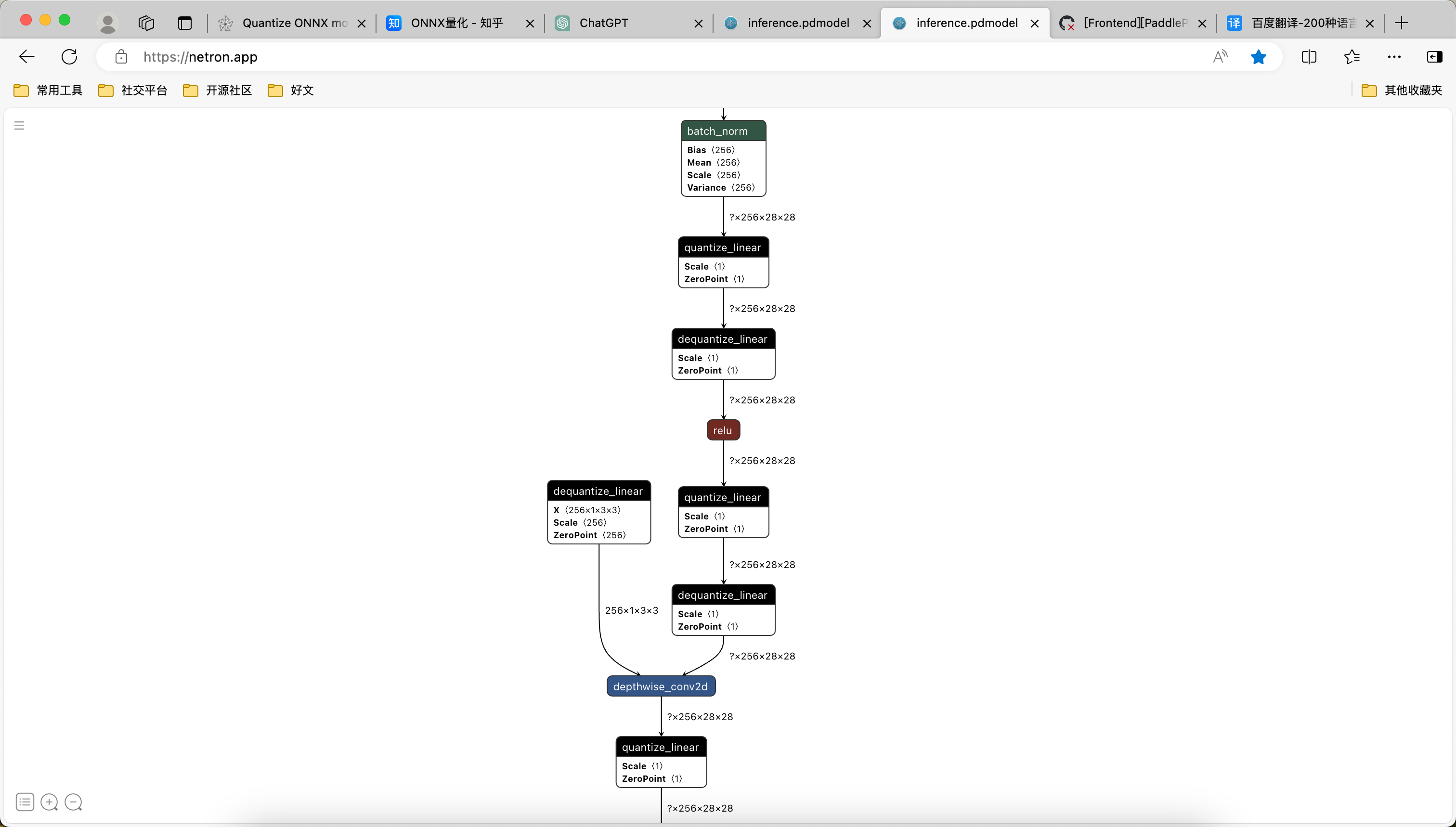
算法
一眼顶针, 鉴定为树形 \(\rm{dp}\)
套路的, 设 \(f_{i, 0/1}\) 表示以 \(i\) 为根的子树, 是否加强 \(i\) 的最大点权和
状态转移方程为
\[\begin{cases}
\displaystyle f_{u, 1} \gets \sum_{v \in \rm{Son}(u)} \max(f_{v, 0}, f_{v, 1} - 2c) + Val_u \\
\displaystyle f_{u, 0} \gets \sum_{v \in \rm{Son}(u)} \max(f_{v, 0}, f_{v, 1})
\end{cases}\]
代码
无实现难度, 不写
总结
注意两头都要影响, 因此是 \(2c\)