本文将重点探讨一种替代传统单一检测器的方法:不是采用单一检测器分析数据集的所有特征,而是构建多个专注于特征子集(即子空间)的检测器系统。
在表格数据的异常检测实践中,我们的目标是识别数据中最为异常的记录,这种异常性可以相对于同一数据集中的其他记录衡量,也可以相对于历史数据进行评估。
在实际应用中,寻找最具意义的异常面临着多重挑战。首要的问题是缺乏一个标准的统计异常性定义,无法明确界定哪些数据异常应被视为最显著。此外,最相关(不一定是统计上最异常)的异常往往依赖于具体项目背景,且可能随时间动态变化。
从技术层面来看,异常检测还面临着一系列挑战,其中最显著的是处理高维数据时遇到的问题。维度灾难对异常检测的影响是多方面的,其中最关键的是使距离度量变得不可靠。大量异常检测算法依赖于计算记录间的距离来识别异常 - 即找出那些与少数记录相似但与大多数记录显著不同的数据点:具体而言,就是与少量其他记录距离近但与大多数记录距离远的数据点。
举例来说,在一个包含40个特征的数据表中,每条记录可以被视为40维空间中的一个点,其异常程度可以通过与该空间中其他点的距离关系来评估。这就需要一种计算记录间距离的方法。常用的度量方式包括欧氏距离等(假设数据为数值型或已转换为数值形式)。因此每条记录的异常程度通常基于其与数据集中其他记录的欧氏距离来衡量。
这种距离计算方法在处理高维数据时往往会失效。因为即使在特征数量仅为十到二十个时就可能出现问题,而在三十或四十个以上特征的情况下,这个问题几乎必然存在。
,目前主流的异常检测器大多属于数值型多变量检测器 - 这类检测器假设所有特征均为数值型,且通常同时处理全部特征。典型如LOF(局部异常因子)和KNN(k近邻),这两种使用最广泛的检测器都基于记录在高维空间中的距离关系来评估其异常性。
基于数据点间距离的异常检测示例
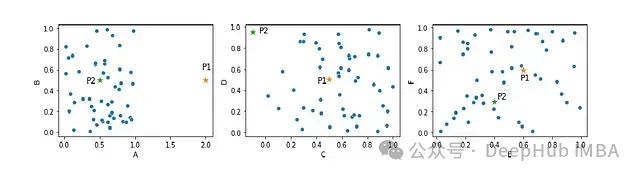
下面的可视化图表。这是一个包含六个特征的数据集的三个二维散点图展示。其中包含两个可以合理判定为异常值的点:P1和P2。
先看点P1,其在特征A维度上显著偏离其他数据点的分布。从单一特征A的角度来看,P1可以明确地被标识为异常值。但是当检测器同时考虑所有六个维度计算点间距离时,由于高维空间距离计算的特性,P1的异常性可能不再那么显著。这是因为P1在其他五个特征维度上表现出正常的分布特征,因此在6维空间中其与其他点的整体距离可能落在正常范围内。
这种基于点间距离的异常检测方法仍具有其合理性:P1和P2之所以被认定为异常值,是因为它们至少在某些维度上与数据集的主体显著分离。
https://avoid.overfit.cn/post/62eaac296ae24672af837a9e420cf1dc