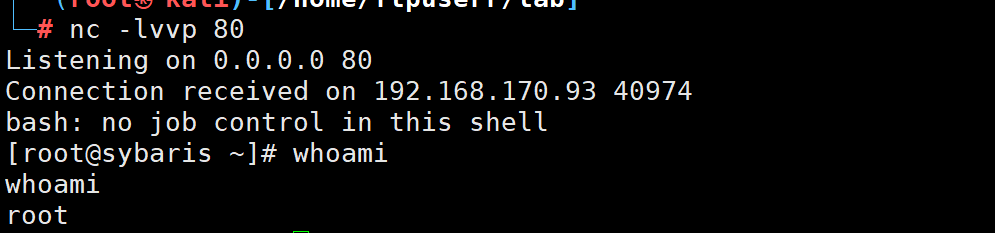
我们设 \(dp_{x,y}\) 表示上一个红色是 \(x\),上一个蓝色是 \(y\) 时最大的价值。
容易发现转移为 \(dp_{a_i,x}=\max\limits_{j=1}^k dp_{k,x}+[k=a_i]a_i,dp_{x,a_i}=\max\limits_{j=1}^k dp_{x,k}+[k=a_i]a_i\)。其中 \(k\) 是值域。
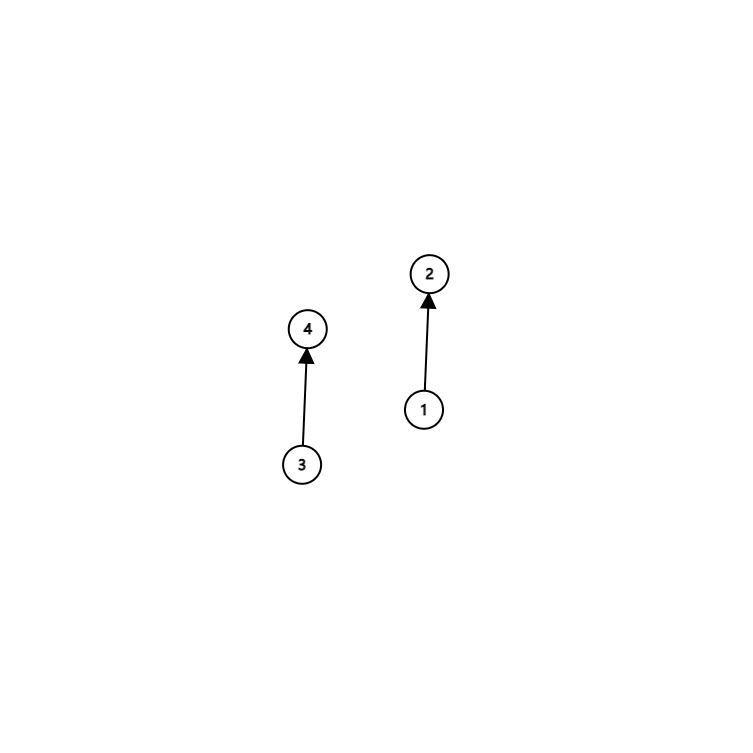
容易发现,转移完后的 \(dp\) 数组中有值的位置是一个十字架(如下图)。
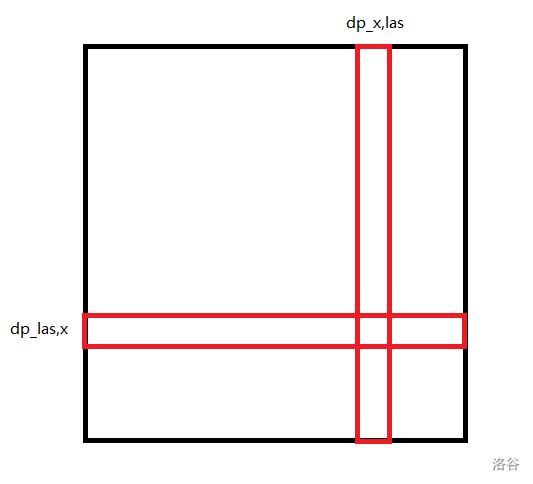
我们考虑直接维护十字架上的值并对其进行转移。
考虑若 \(a_i=a_{i-1}\),相当于全局加上 \(a_i\),打一个标记即可。
若 \(a_i\not=a_{i-1}\),记 \(las=a_i,f_{i,x}=dp_{a_i,x},g_{i,x}=dp_{x,a_i}\)。
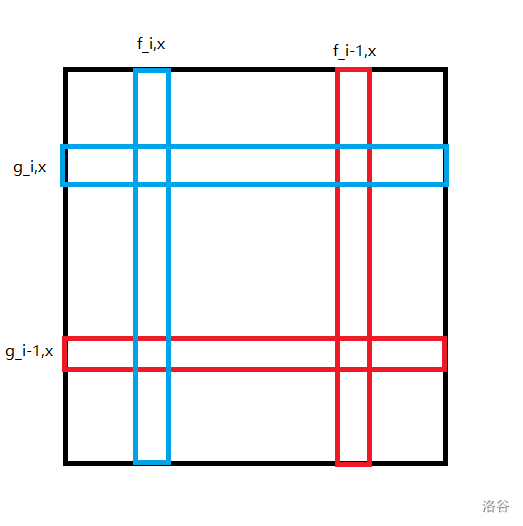
容易发现转移:
\[\begin{array}{c}
f_{i,x}&=&f_{i-1,x}\\
f_{i,las}&=&\max(g_{i-1,a_i}+a_i,maxg)\\
g_{i,x}&=&g_{i-1,x}\\
g_{i,las}&=&\max(f_{i-1,a_i}+a_i,maxf)\\
f_{i,a_i}=g_{i,a_i}&=&\max(f_{i,a_i},g_{i,a_i})
\end{array}
\]
直接维护即可,复杂度 \(O(T(n+V))\)