题目
题目描述
给定一棵树,对于每一个点,输出离它最远的点到它的距离。
输入格式
第一行包含整数 \(n\)。
接下来 \(n-1\) 行,每行包含两个整数 \(a_i,b_i\),表示点 \(a_i\) 和 \(b_i\) 之间存在一条边。
输出格式
输出一行 \(n\) 个整数,第 \(i\) 个数表示离节点 \(i\) 最远的点到它的距离。
样例
输入数据#1
8
1 5
1 4
6 3
2 6
6 1
3 7
4 8
输出数据#2
3 4 4 4 4 3 5 5
数据范围
- 对于 \(20\%\) 的数据:\(1≤n≤10\)。
- 对于 \(60\%\) 的数据:\(1≤n≤10^3\)。
- 对于 \(100\%\) 的数据:\(1≤n≤10^5\),\(1≤a_i,b_i≤n\)。
思路分析
树的直径好题。
我们如果对每个点都跑一遍树的直径 dfs,时间复杂度 \(O(n^2)\),超时。数据范围 \(n\leq10^5\) 显然只允许我们跑一遍树的直径 dfs。
其实,我们只需先找到一条直径,然后对于每个点,比较两个端点哪个距离该点较远即可。
现在求点 \(u\) 最远的点到它的距离,记为 \(ans\),跑树的直径 dfs 后得到直径 \(a\to b\),分类讨论:
若点 \(u\) 不在直径 \(a\to b\) 的路径上,如下图:
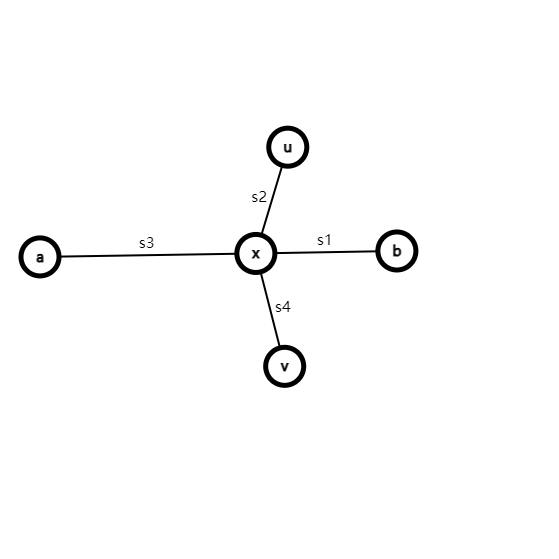
反证法:
假设有点 \(v\) 是点 \(u\) 最远的点,距离为 \(s_2+s_4\),直径的端点 \(a\) 到点 \(u\) 的距离为 \(s_2+s_3\),则:
\[s_2+s_4>s_2+s_3
\]
解得 \(s_4>s_3\)
所以 \(x\to v\) 的路径比 \(x\to a\) 的路径更长,直径则应为 \(s_1+s_4\),与树的直径是 \(a\to b\) 矛盾,显然不存在。
若点 \(u\) 在直径 \(a\to b\) 的路径上:
证明如上,其中 \(s_2=0\),显然也不存在。
证毕。
\(\texttt{code}\)
/*Written by smx*/
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define QAQ cout<<"QAQ\n";
const int MAXN=1e5+5,inf=1e18,mod=1e9+7;
int n;
vector<int> g[MAXN];
int dist[MAXN],d[MAXN];
int dfs(int now,int fa){int ans=now;for(auto x:g[now]){if(x==fa){continue;}dist[x]=dist[now]+1;int d=dfs(x,now);if(dist[d]>dist[ans]){ans=d;}}return ans;
}
signed main(){//freopen(".in","r",stdin);//freopen(".out","w",stdout);ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin>>n;for(int i=1;i<n;i++){int u,v;cin>>u>>v;g[u].push_back(v);g[v].push_back(u);}int u,v;u=dfs(1,0);dist[u]=0;v=dfs(u,0);for(int i=1;i<=n;i++){d[i]=dist[i];}dist[v]=0;dfs(v,0);for(int i=1;i<=n;i++){cout<<max(d[i],dist[i])<<" ";}return 0;
}