前情概要
在和同事研讨下述题目的解答时,碰到了一些困难,思路不太好把握,探索一番,做个记录。
案例分析

总基调:题目要求清洁钢球能擦净凹槽的最底部,则钢球要和能经过抛物线的底部[顶点],当钢球半径最大时,则钢球与抛物线相切于底部的顶点 .
探索1️⃣:从学科网和菁优网下载答案参考学习,基本上看不大懂,感觉选择的角度是从形上容易切入思考,但在数上运算时不太好理解,干脆放弃,思考从数上入手思考;一点小反思,即使网上老师的作答,也不要一味的迷信,如果你有多个网络信息源,可以下载多个解答,在比较中选优[我也曾经给菁优网解答过题目,前几年最贵的导数类解答题也只开价 \(4.5\) 元,而且要求多,有分析,有解答,有配套的图象,还得有解后反思,太麻烦,解答了 \(100\) 多个题目后放弃了] .
探索2️⃣:从图形上入手分析,做出经过球心的截面图形,建系如图所示,根据对称性设圆的半径最大时圆心为 \(A\)\((0,r)\),\((r>0)\),抛物线上任意一点为 \(P\)\((x,y)\),则 \(y\)\(\geqslant\)\(0\),
由图可知,抛物线上的任意一点一定满足条件:\(|PA|\)\(\geqslant\) \(r\) [1],
为运算简单,采用这样的运算思路,\(|PA|^2\)\(\geqslant\)\(r^2\),即 \((x-0)^2\)\(+\)\((y-r)^2\)\(\geqslant\)\(r^2\),
将 \(x^2\)\(=\)\(4y\) 代入,打开整理得到,\(y^2\)\(+\)\(4y\)\(-\)\(2ry\)\(\geqslant\)\(0\),
即 \(y\)\(\cdot\)\((y+4-2r)\)\(\geqslant\)\(0\),由题目可知\(y\)\(\geqslant\)\(0\),由 符号法则 可知,\(y\)\(+\)\(4\)\(-\)\(2r\)\(\geqslant\)\(0\),
即 \(2r\)\(\leqslant\)\(y\)\(+\)\(4\),即 \(r\)\(\leqslant\)\(\cfrac{y}{2}\)\(+\)\(2\),
当 \(y\) 取最小值 \(0\) 时,\(r\)\(\leqslant\)\(2\),则 \(r\) 的取值范围是 \((0,2]\),故 \(r\) 的最大值为 \(2\) . 选择 \(C\) 选项 .
- 相关补充:基本采用了大神 Math173 的做法,请参阅 相似解答
探索3️⃣:刚好那几天接触了个 纳米搜索,想到用这个题目的图片练手,既学习纳米搜索的使用,也想看看所谓的 Ai 搜索到底功能如何,你别说,还真是有收获,由此看到一片不一样的天地:我的搜索结果图片为证,是为记
设钢球的圆心为 \(A(0,r)\) ( \(r\) 为钢球半径),当钢球半径最大时,钢球与抛物线相切,
设切点坐标为 \(P(x,y)\) ,对于抛物线 \(x^2\)\(=\)\(4y\) ,其导数为 \(y^{\prime}\)\(=\)\(\cfrac{x}{2}\) ,则在点 \((x, y)\) 处的切线斜率为 \(\cfrac{x}{2}\),
同时,圆心 \(A(0, r)\) 与切点 \(P(x,y)\) 连线的斜率为 \(k_{_{AP}}\)\(=\)\(\cfrac{y-r}{x}\),[2]
因为切线 \(l\) 与直线 \(AP\) 的连线垂直,所以它们斜率乘积为 \(-1\) ,
即 \(\cfrac{x}{2}\)\(\times\)\(\cfrac{y-r}{x}\)\(=\)\(-1\) ,化简得 \(y\)\(-\)\(r\)\(=\)\(-2\) ,即 \(y\)\(=\)\(r\)\(-\)\(2①\),
又因为 \((x,y)\) 在抛物线上,所以 \(x^2\)\(=\)\(4y\) ,
将 \(y\)\(=\)\(r-2\) 代入 \(x^2\)\(=\)\(4y\) 可得 \(x^2\)\(=\)\(4(r-2)②\) ,
将 \(①②\) 代入圆的方程: \((x-0)^2\)\(+\)\((y-r)^2\)\(=\) \(r^2\) 中,即 \(4(r-2)\)\(+\)\((r-2-r)^2\)\(=\)\(r^2\),
整理得到,\((r-2)^2\)\(=\)\(0\),解得 \(r\)\(=\)\(2\),[将其代入 \(①②\) 可得切点坐标为 \((0,0)\)]
故清洁钢球的最大半径为 \(2\) ,选择 \(C\) 选项 .
延申练习

解析:设清洁钢球的半径为 \(r\),则其球心坐标为 \(P(0,1+r)\),则双曲线上的所有点到 \(P\) 的距离不小于 \(r\),设双曲线上的点为 \(Q(x_0, y_0)\),
则 \(|PQ|^2\)\(\geqslant\)\(r^2\)\(\Longleftrightarrow\)\(x_0^2\)\(+\)\((y_0-1-r)^2\)\(\geqslant\)\(r^2\)\(\Longleftrightarrow\)\(y_0^2\)\(-1\)\(+\)\((y_0-1-r)^2\)\(-\)\(r^2\)\(\geqslant\)\(0\)
整理可得 \(2\)\((y_0-r)\)\((y_0-1)\)\(\geqslant\)\(0\)\(\Longleftrightarrow\)\(r\)\(\leqslant\)\(y_0\),
因此 \(r\) 的最大值为 \(y_0\) 的最小值,则清洁钢球的最大半径为 \(1\),故选 \(A\) .
[备注]:对高中学生而言,以下内容是超纲的,我也不清楚这个公式。
根据曲线的曲率半径的计算公式 \(R=\left|\cfrac{\left(1+f^{\prime 2}(x)\right)^{\frac{3}{2}}}{f^{\prime \prime}(x)}\right|\),可得双曲线在底部的曲率半径为 \(1\),因此清洁钢球的最大半径为 \(1\) .
这是这类题目的题眼,虽然到现在我们不知道本题目该如何控制,不着急,到最后就柳暗花明了。原因是所有的从形上体现出来的信息一定有与之对应的数的表达形式,就是我们一时半会儿没有找到而已。 ↩︎
目前,这种思路有个漏洞是,当切点为坐标原点时,切线的斜率为 \(0\),而直线 \(AP\) 的斜率是不存在的。 ↩︎
 关于抛物线和圆的位置关系的问题探索和引申
关于抛物线和圆的位置关系的问题探索和引申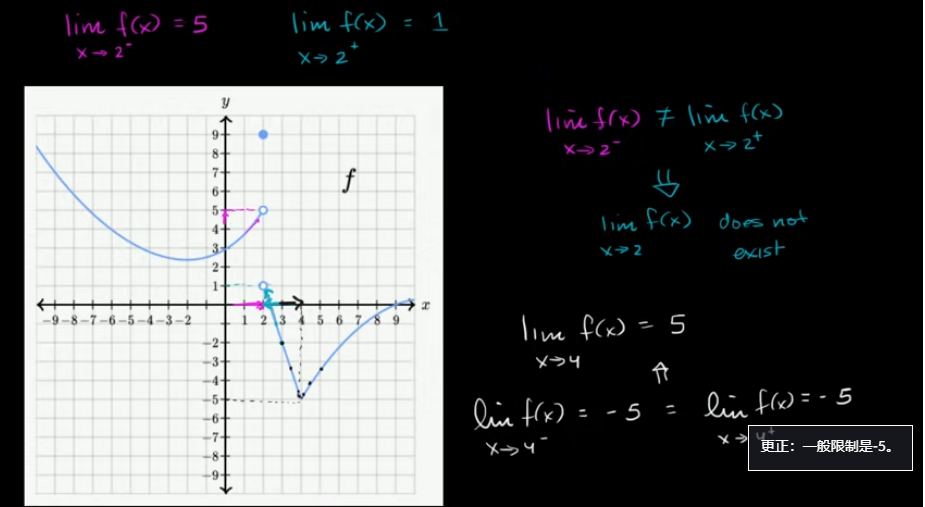


![LeetCode 509[斐波那契数]](https://img2024.cnblogs.com/blog/3512406/202412/3512406-20241204173106567-336518070.png)