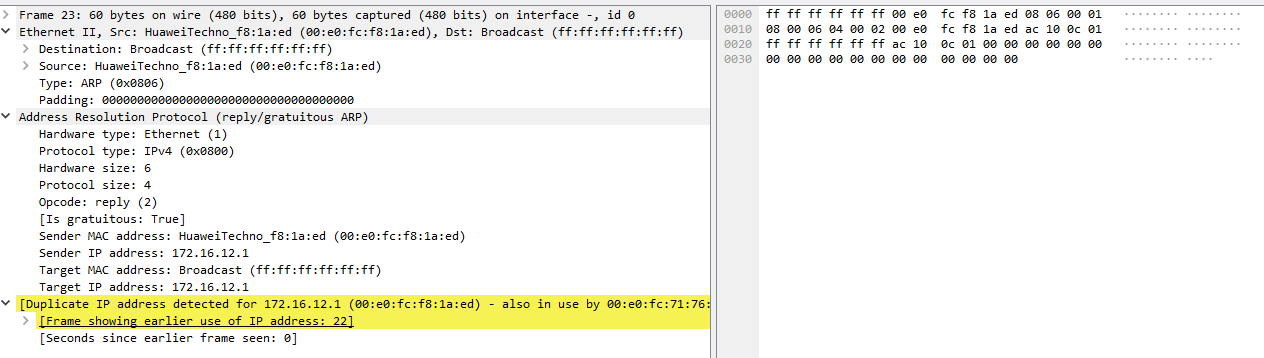
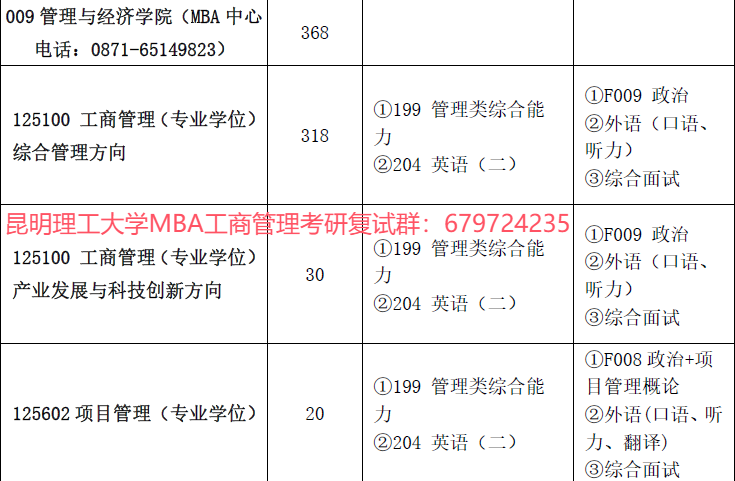
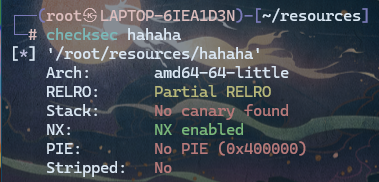
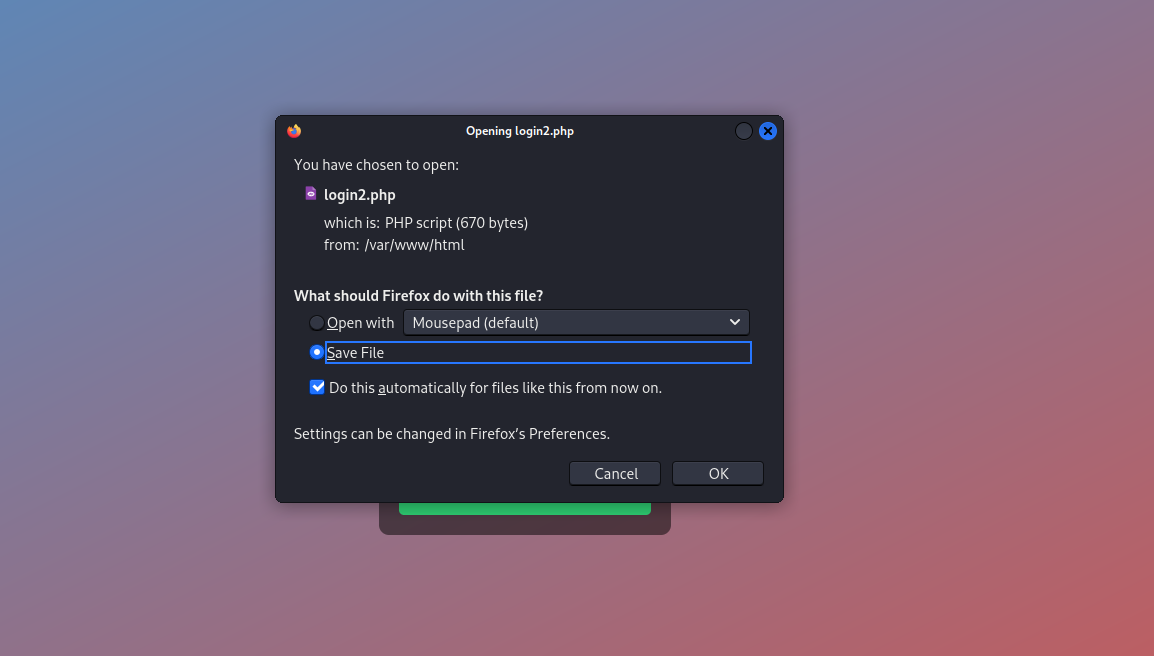
Pohlig-Hellman算法——用中国剩余定理考虑离散对数问题
除了作为定理和算法外,建议读者将中国剩余定理看作一种思维方式。如果 $ m = m_1 \cdot m_2 \cdot \cdots \cdot m_t $ 是一组两两互质的整数的乘积,那么中国剩余定理告诉我们,求解关于 $ m $ 的方程实际上等价于分别求解关于 $ m_i $ 的方程,然后将这些解结合起来得到关于 $ m $ 的解。
在离散对数问题(DLP)中,我们需要求解方程
在这个问题中,模数 $ p $ 是素数,中国剩余定理似乎与问题无关。然而,回想一下,解 $ x $ 仅在模 $ p-1 $ 下确定,因此我们可以将解看作是位于 $ \mathbb{Z}/(p-1)\mathbb{Z} $ 中。这暗示着 $ p-1 $ 的质因数分解可能在确定离散对数问题在 $ \mathbb{F}_p^* $ 中的难度上起到作用。
比如,如果 \(p-1\) 的质因数分解为不同素数的一次幂的乘积,这个时候利用中国剩余定理可以把求解 \(x(\bmod p-1)\) 转化为去求解一个模数均为素数的一次模同余方程组。解一次模同余方程自然是要比解高次模同余方程简单。
更一般地说,如果 $ G $ 是一个群,且 $ g \in G $ 是一个阶为 $ N $ 的元素,那么方程 $ g^x = h $ 在 $ G $ 中的解仅在模 $ N $ 下确定,因此从中国剩余定理的观点看, $ N $ 的质因数分解会影响离散对数问题求解的难度。这个想法正是Pohlig-Hellman算法的核心。
我们将对于任意群 $ G $ 进行陈述和证明。但是,如果你更习惯于处理模 $ p $ 下的整数问题,你可以直接将 $ G $ 替换为 $ \mathbb{F}_p^* $。
引理 1 使用扩展欧几里得算法求解 \(gcd(a,b)(a>b\geq 1)\) 的时间复杂度为 \(O(\log b)\)
证明 (若 \(a<b\) 我们只需多做一次模运算, 若 \(b=0\) 或 \(a=b\) 模运算的次数分别为 \(0\) 和 \(1\) ), 构造数列 \(\left\{u_n\right\}: u_0=a, u_1=b, u_k=u_{k-2} \bmod u_{k-1}(k\geq2)\), 显然, 若算法在第 \(n\) 次模运算时终止, 则有 \(u_n=\operatorname{gcd}(a, b), u_{n+1}=0\). 我们比较数列 \(\left\{u_n\right\}\) 和菲波那契数列 \(\left\{F_n\right\}, F_0=1\leq u_n, F_1=1\leq u_{n-1}\), 又因为由 \(u_k \bmod u_{k+1}=u_{k+2}\), 可得 \(u_k\geq u_{k+1}+u_{k+2}\), 则 \(F_2=F_0+F_1\leq u_n+u_{n-1}\leq u_{n-2}\)由数学归纳法容易得到 \(F_{k}\leq u_{n-k}(\forall 0\leq k \leq n)\), 于是得到 \(a=u_0 \geq F_n, b=u_1 \geq F_{n-1}\). 也就是说如果欧几里得算法需要做 \(n\) 次模运算, 则 \(b\) 不小于 \(\mathrm{F}_{n-1}\). 换句话说, 若 \(b<F_{n-1}\), 则算法所需模运算的次数必定小于 \(n\). 所以模运算的次数为 \(O(\log b)\).
注:\(F_n=\frac{1}{\sqrt{5}}\left(\phi^n-(1-\phi)^n\right) \approx \frac{\phi^n}{\sqrt{5}}\) 其中: \(\phi=\frac{1+\sqrt{5}}{2}\) 是黄金分割率(约为 1.61803)。
换句话说,把扩展欧几里得算法的每一步结果从 \(\gcd (a,b)\) 开始倒过来看,增长速度大于斐波那契数列。
推论:使用扩展欧几里得算法实现中国剩余定理的求解的时间复杂度为 \(O(\log N)\),其中 \(N\) 为所有两两互素的模数的乘积。
定理 2(Pohlig–Hellman 算法)
设 $ G $ 是一个群,假设我们有一个算法可以解决 $ G $ 中任何阶为素数的幂次的元素的离散对数问题。具体来说,若 $ g \in G $ 的阶为 $ q^e $,我们假设能够在 $ O(S_{q^e}) $ 步内求解 $ g^x = h $ 的离散对数问题,其中 $ S_{q^e} $ 是与 $ q^e $ 相关的某个函数。
由定理 \(5\),\(S_{q^e}\) 可以取到 \(O(q^{e/2}\log q^e)\approx O(q^{e/2})\)
现在,设 $ g \in G $ 是阶为 $ N $ 的元素,并假设 $ N $ 可以分解为素数幂的积形式:
那么,离散对数问题 $ g^x = h $ 可以在
证明
由中国剩余定理,
现在的问题是
我们要在 \(()\) 中填入一些具体的元素,使得我们可以再次使用中国剩余定理对右边的方程组进行具体的求解。
这时需要利用定理所给的条件————“假设我们有一个算法可以解决 $ G $ 中任何阶为素数的幂次的元素的离散对数问题”来构造 \(()\) 中的具体的元素。
设 \(x\equiv y_i(\bmod q_i^{e_i})\),令 \(g_i=g^{N/q_i^{e_i}}\),\(h_i=h^{N/q_i^{e_i}}\),现考虑离散对数问题 \(g_i^y=h_i\) 的解,记作 \(y_i\)。
则易知 \(y_i\) 是模 \(q_i^{e_i}\) 定义的,而恰好 \(x(\bmod q_i^{e_i})\) 也是模 \(q_i^{e_i}\) 定义的。将 \(x\) 代入方程 \(g_i^y=h_i(\forall 1\leq i\leq t)\) 发现 \(x\) 确实是解。于是 \(x \equiv y_i(\bmod q_i^{e_i})\).
因此
此时再对右边使用中国剩余定理即可求得 \(x(\bmod N)\).
对上述进行归纳可得算法步骤:
-
对于每个 $ 1 \leq i \leq t $,计算 $ g_i $ 和 $ h_i $:
\[g_i = g^{N/q_i^{e_i}} \quad \text{和} \quad h_i = h^{N/q_i^{e_i}}. \]注意到 $ g_i $ 的阶为 $ q_i^{e_i} $,因此我们可以使用给定的算法求解离散对数问题:
\[g_i^{y} = h_i. \]令 $ y_i $ 为该方程的解。
-
使用中国剩余定理解以下同余方程组:
\[x \equiv y_1 \pmod{q_1^{e_1}}, \quad x \equiv y_2 \pmod{q_2^{e_2}}, \quad \dots, \quad x \equiv y_t \pmod{q_t^{e_t}}. \quad (2.15) \]
该过程的运行时间是显而易见的。步骤 \(1\) 对每个 $ i $ 需要 $ O(S_{q_i^{e_i}}) $ 步,步骤 \(2\) 使用中国剩余定理需要 $ O(\log N) $ 步。在实际应用中,中国余数定理的计算通常与离散对数计算相比可以忽略不计。\(\square\)
引理 3(模运算的复杂度)
模运算(取模运算)的时间复杂度取决于我们如何执行该操作以及操作数的大小。模运算的基本形式是:
其中 $ a $ 是被除数,$ m $ 是模数,要求计算 $ a $ 除以 $ m $ 的余数。
-
传统的除法方法:
- 模运算本质上是计算整数除法后的余数: $ a \div m $ 然后取余。
- 在计算机中,整数除法的时间复杂度通常是与被除数的位数(或大小)成正比的。
- 对于 $ a $ 和 $ m $ 都是 $ k $ 位数的整数,传统除法方法的时间复杂度是 $ O(k^2) $,即 $ O(\log^2 a) $,其中 $ a $ 是被除数, $ k $ 是 $ a $ 和 $ m $ 的二进制位数。
-
高效的除法算法:
- 对于大数模运算,某些优化算法如快速模乘法(Fast Modular Multiplication)可以将除法和模运算的复杂度降低到 $ O(k \log k) $。
- 在现代计算中,许多情况下会使用更高效的数值算法,比如基于蒙哥马利算法(Montgomery multiplication)或卡拉比-卡拉法(Karatsuba)乘法的优化算法,这些算法能在多项式时间内高效计算大数的模。
-
模幂运算的时间复杂度:
对在许多加密算法(如RSA加密)中,常常需要计算模幂运算,即计算:
这种运算的时间复杂度与幂的大小和模数有关,通常使用快速幂算法来实现。
- 快速幂算法的时间复杂度是 $ O(\log b) $,其中 $ b $ 是指数。因为快速幂算法通过二分法分解指数 $ b $,使得计算复杂度大大减少。每一轮操作都是对指数进行二分,最终使得运算次数为 $ \log b \(。 \)\square$
引理 4 (离散对数问题复杂度的平凡上界):
设 $ G $ 是一个群,$ g \in G $ 是阶为 $ N $ 的元素,那么离散对数问题
可以在 $ O(N) $ 步内解决。\(\square\)
如果我们在 $ F_p^* $ 中工作,那么每次计算 $ g^x \mod p $ 需要 $ O((\log p)^k) $ 次计算操作,其中常数 $ k $ 和隐含的大 $ O $ 常数依赖于计算机和用于模乘的算法。因此,总的计算步骤数,或称运行时间,是 $ O(N(\log p)^k) \(。通常,\) O((\log p)^k) $ 所贡献的因子可以忽略不计,因此我们将其省略,直接称运行时间为 $ O(N) $。
我们将介绍 Shanks 提出的离散对数算法,这是一个碰撞算法。碰撞算法的运行时间略大于 $ O(\sqrt{N}) $ 步,这在 $ N $ 较大时,相较于 $ O(N) $ 是一个巨大的节省。
碰撞算法(Collision Algorithm)是指在密码学中,试图找到两个不同的输入数据,它们经过某个哈希函数处理后产生相同的哈希值的算法。简单来说,碰撞就是两个不同的输入“碰撞”到同一个输出。
定理 5 (Shanks 的小步–大步算法):
设 $ G $ 是一个群,且 $ g \in G $ 是阶为 $ N \geq 2 $ 的元素。以下算法在 $ O(\sqrt{N} \cdot \log N) $ 步内解决离散对数问题 $ g^x = h $。
- 令 $ n = 1 + \lfloor \sqrt{N} \rfloor \(,特别地,\) n > \sqrt{N} $。
- 创建两个列表:
- 列表 \(1\):$ e, g, g^2, g^3, \dots, g^n $
- 列表 \(2\):$ h, h \cdot g^{-n}, h \cdot g^{-2n}, h \cdot g^{-3n}, \dots, h \cdot g{-n2} $
- 查找两个列表之间的匹配项,假设为 $ g^i = h \cdot g^{-jn} $。
- 则 $ x = i + jn $ 是 $ g^x = h $ 的解。
证明:
我们首先做一些观察。首先,在创建列表 \(2\) 时,我们首先计算 $ u = g^{-n} $,然后通过计算 $ h, h \cdot u, h \cdot u^2, \dots, h \cdot u^n $ 来构建列表 \(2\)。所以,创建两个列表大约需要 $ 2n $ 次乘法运算。其次,假设存在匹配项,我们可以通过标准的查找算法,在 $ O(n\log n) $ 步内找到匹配项,因此第 3 步需要 $ O(n\log n) $ 步。因此,整个算法的总运行时间为 $ O(n \log n) = O(\sqrt{N} \log N) $。在这最后一步,我们使用了 $ n \approx \sqrt{N} $ 的事实,因此有
为了证明该算法有效,我们必须证明列表 \(1\) 和列表 \(2\) 总是有一个匹配项。为此,假设 $ x $ 是离散对数问题 $ g^x = h $ 的解,并将 $ x $ 表示为
我们知道 $ 1 \leq x < N $,因此
因此我们可以将方程 $ g^x = h $ 重写为
因此,$ g^r $ 在列表 \(1\) 中,且 $ h \cdot g^{-qn} $ 在列表 \(2\) 中,这表明列表 \(1\) 和列表 \(2\) 有一个共同元素。