目录
一.题目描述
二.思路分析
三.代码编写
一.题目描述
将x减到0的最小操作数

题目要求我们在数组的两端不断地取值,使得取出的数之和等于x,问我们最少需要取几次。
也就是说,在两边取两个区间,使得这两个区间的之和等于x,求这两个区间长度之和最小是多少。
两个区间研究起来比较麻烦,正难则反,我们可以转化为研究两侧区间所围的区间,那么只需找到满足条件的最长区间,这个条件就是区间之和为sum-target(sum是整个数组的和),结果就是数组的长度减去求得的len。
二.思路分析
两层for循环暴力枚举所有的区间,找到符合条件的区间,通过比较得到最长的区间长度,从而得到结果。代码就不具体实现了。
使用滑动窗口优化,首先要证明right不需要回退
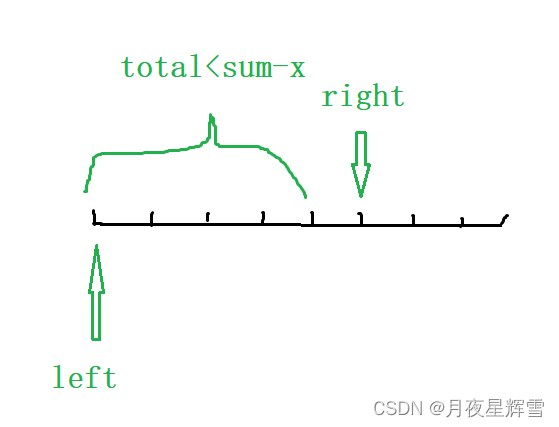
right不断向后移动,当移动到图中位置时,区间之和total>= sum-x, right停了下来,(潜台词是[left, right - 1]区间的和是小于total的)。此时应该判断total是否等于sum-x, 如果是就更新结果。隐含条件:。
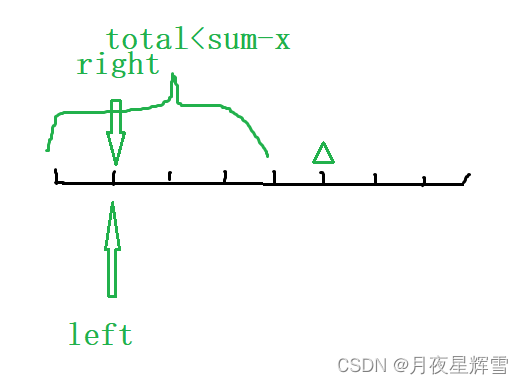
按照暴力枚举策略 ,left向后移动一步,right回退。但是最终right还是会回到原处。因为图中大括号对应的区间之和是不满足要求的,right会一直向右移动。故right没有必要往回退,留在原地即可。
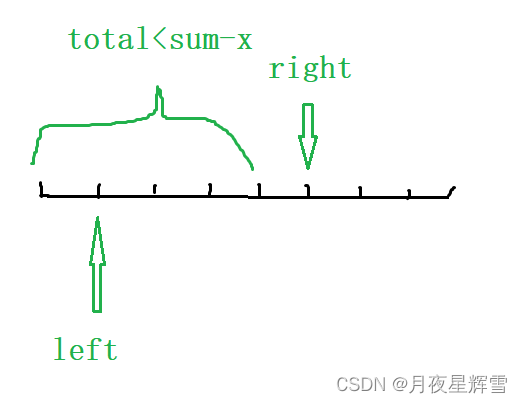
那么此时的区间之和是否小于sum-x呢?不确定,因为可能跳过的是一个很小的数,区间之和仍然>=sum-x,此时right没有必要向后枚举了,因为区间再往后扩展,和肯定大于sum-x了。所以让left继续向后移动,直到total <sum-x时,right再向后移动。
所以判断是一个循环的逻辑,不能用if简单地只判断一次。
三.代码编写

其中更新结果时total应该等于target,故可以再判断条件成立,出窗口之前判断total是否等于target,如果等于就更新结果。
class Solution {
public:int minOperations(vector<int>& nums, int x) {int sum = 0;for (auto e : nums){sum += e;}int target = sum - x;int n = nums.size();int len = -1;int left = 0, right = 0;int total = 0;//统计窗口内所有数的和while (right < n){//进窗口total += nums[right];//判断while (total >= target){//更新结果if (total == target){len = max(len, right - left + 1);}//出窗口total -= nums[left++];}right++;}return len == -1 ? -1 : n - len;}
};当你怀着激动的心情提交代码时,发现到第6个用例就挂了


这种错误提示,八成是越界访问了。模拟代码的执行逻辑,最后发现确实是left越界了。原因在于target是个负数,当right移动到n-1位置,left移动到n位置时,total恰好等于0,但还是大于等于target,故还要出窗口,此时left就越界访问报错了。所以targe小于等于0时需要特殊处理。
当target小于0时,直接返回-1,因为所有数都是正整数,不可能有结果。当target=0时,说明sum=x,直接返回数组长度即可。
class Solution {
public:int minOperations(vector<int>& nums, int x) {int sum = 0;for (auto e : nums){sum += e;}//越界情况单独处理int target = sum - x;if (target < 0){return -1;}if (target == 0){return nums.size();}int n = nums.size();int len = -1;int left = 0, right = 0;int total = 0;//统计窗口内所有数的和while (right < n){//进窗口total += nums[right];//判断while (total >= target){//更新结果if (total == target){len = max(len, right - left + 1);}//出窗口total -= nums[left++];}right++;}return len == -1 ? -1 : n - len;}
};事实上,还可以将更新结果的操作放在while循环外面,这时只需把循环的条件改为total>target。当程序通过while循环的逻辑后,total要么小于target,要么等于target。此时再进行判断,如果等于就更新结果,这样的逻辑会更加简单,而且此时target=0的情况也不会越界访问了。
class Solution {
public:int minOperations(vector<int>& nums, int x) {int sum = 0;for (auto e : nums){sum += e;}//越界情况单独处理int target = sum - x;if (target < 0){return -1;}int n = nums.size();int len = -1;int left = 0, right = 0;int total = 0;//统计窗口内所有数的和while (right < n){//进窗口total += nums[right];//判断while (total > target){//出窗口total -= nums[left++];}//更新结果if (total == target){len = max(len, right - left + 1);}right++;}return len == -1 ? -1 : n - len;}
};时间复杂度O(n)