题面
题目描述
NOI2130 即将举行。为了增加观赏性,CCF 决定逐一评出每个选手的成绩,并直播即时的获奖分数线。本次竞赛的获奖率为 $w%$,即当前排名前 $w%$ 的选手的最低成绩就是即时的分数线。
更具体地,若当前已评出了 $p$ 个选手的成绩,则当前计划获奖人数为 $\max(1, \lfloor p \times w %\rfloor)$,其中 $w$ 是获奖百分比,$\lfloor x \rfloor$ 表示对 $x$ 向下取整,$\max(x,y)$ 表示 $x$ 和 $y$ 中较大的数。如有选手成绩相同,则所有成绩并列的选手都能获奖,因此实际获奖人数可能比计划中多。
作为评测组的技术人员,请你帮 CCF 写一个直播程序。
输入格式
第一行有两个整数 $n, w$。分别代表选手总数与获奖率。
第二行有 $n$ 个整数,依次代表逐一评出的选手成绩。
输出格式
只有一行,包含 $n$ 个非负整数,依次代表选手成绩逐一评出后,即时的获奖分数线。相邻两个整数间用一个空格分隔。
样例 #1
样例输入 #1
10 60
200 300 400 500 600 600 0 300 200 100
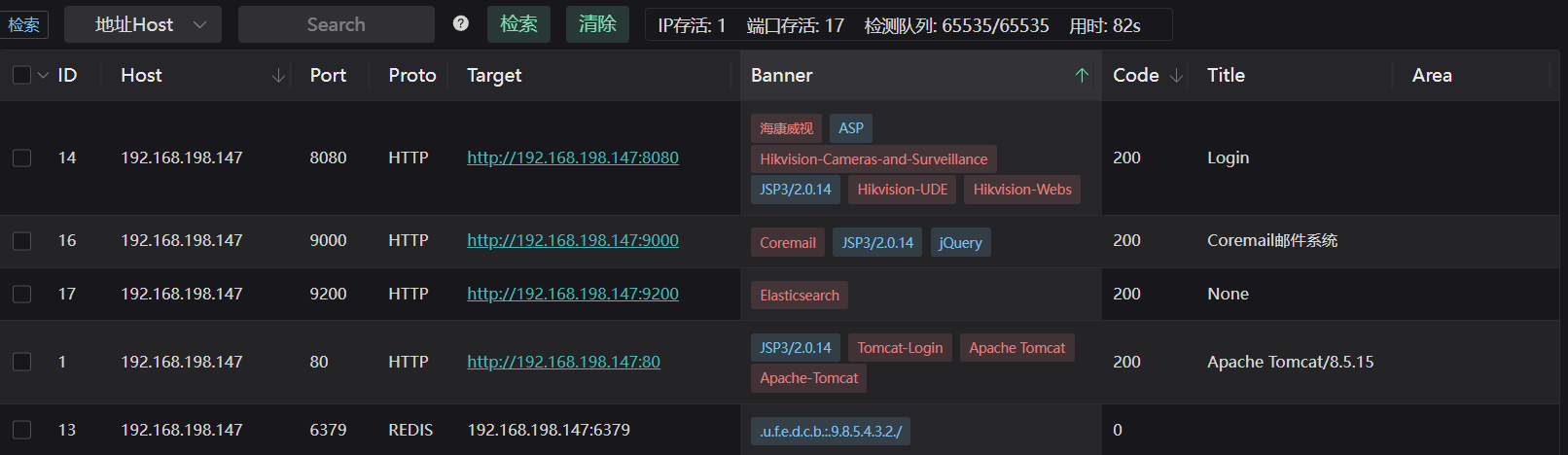
样例输出 #1
200 300 400 400 400 500 400 400 300 300
样例 #2
样例输入 #2
10 30
100 100 600 100 100 100 100 100 100 100
样例输出 #2
100 100 600 600 600 600 100 100 100 100
提示
样例 1 解释

数据规模与约定
各测试点的 $n$ 如下表:
| 测试点编号 | $n=$ |
|---|---|
| $1 \sim 3$ | $10$ |
| $4 \sim 6$ | $500$ |
| $7 \sim 10$ | $2000$ |
| $11 \sim 17$ | $10^4$ |
| $18 \sim 20$ | $10^5$ |
对于所有测试点,每个选手的成绩均为不超过 $600$ 的非负整数,获奖百分比 $w$ 是一个正整数且 $1 \le w \le 99$。
提示
在计算计划获奖人数时,如用浮点类型的变量(如 C/C++ 中的 float 、 double,Pascal 中的 real 、 double 、 extended 等)存储获奖比例 $w%$,则计算 $5 \times 60%$ 时的结果可能为 $3.000001$,也可能为 $2.999999$,向下取整后的结果不确定。因此,建议仅使用整型变量,以计算出准确值。
思路
按照题意模拟,每有一个人评出成绩就计算有几个人获奖,将成绩从大到小排序并输出第 $\max(1, \lfloor p \times w %\rfloor)$ 个人的成绩。
问题
$10 \le n \le 10^5$ ,若每次读入均排序会超时,最多只能通过一半测试点。
解决方案1
注意到分数的范围最高只有 $600$ ,考虑桶排序。
#include<bits/stdc++.h>
using namespace std;
int a[601],n,w,x;int main()
{scanf("%d%d",&n,&w);for(int i=1;i<=n;i++){scanf("%d",&x),a[x]++;int sum=0;for(int j=600;j>=0;j--){sum+=t[j];if(sum>=max(1,i*w/100)){printf("%d ",j);break;}}}return 0;
}
解决方案2
因为是排序导致的超时,所以理所当然想到使用 STL 中的大小根堆来维护分数。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;ll read()
{ll k,f=1;char c;while((c=getchar())<'0'||c>'9') if(c=='-') f=-1;k=c^48;while((c=getchar())>='0'&&c<='9')k=(k<<3)+(k<<1)+(c^48);return k*f;
}void put(ll k)
{if(k<0) putchar('-'),k=~k+1;if(k>9) put(k/10);putchar(k%10+'0');
}ll n,w,now,las,sco[1000010];
priority_queue<ll,vector<ll>,greater<ll> > q1;
priority_queue<ll,vector<ll>,less<ll> > q2;int main()
{//freopen("live.in","r",stdin);//freopen("live.out","w",stdout);n=read(),w=read();for(ll i=1;i<=n;i++){sco[i]=read();q2.push(sco[i]);if(q1.size()&&q2.size())while(q1.top()<q2.top())q2.push(q1.top()),q1.pop(),q1.push(q2.top()),q2.pop();now=max(1ll,i*w/100);while(q1.size()>now) q2.push(q1.top()),q1.pop();while(q1.size()<now) q1.push(q2.top()),q2.pop();put(q1.top()),putchar(' ');}return 0;
}
(该代码转自洛谷Ink_Bottle的博客, 原址Link ,因为作者倾向于使用桶排序,但这种方法确实更正规。)
提示:距 CSP-J/S 2024 第二轮 还剩 10 天。