01背包+多状态dp
前置知识
dp的四步法(绝对不是水字数):
- 确定状态
- 确定答案
- 确定状态转移方程
- 确定初始状态和边界
P7074 [CSP-J2020] 方格取数
题目中所给出的状态是这样的(图一):
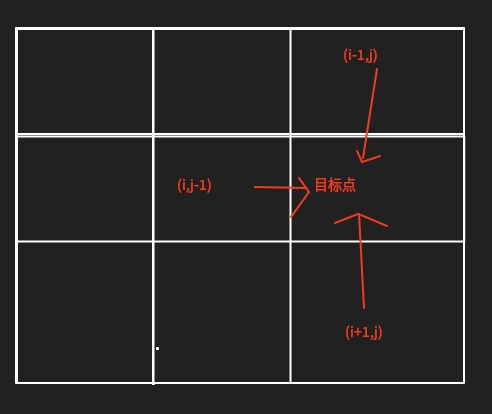
但是这样就会导致一个问题, \(i\) 值会访问空的地方,所以这里会有两种方案:
- 左上角走到右下角(最短路线)
- 三角形取数(题目所给方式)
本体上下之间其实并不存在后效性,因为不能重复经过一个点。
认定一个方向之后只能走原本方向或者右边每一列,行和行之间存在后效性的因为第 \((i,j)\) 的答案可能从第 \(i-1\) 行,第 \(j\) 列到达或者从第 \(i+1\) 行,第 \(j\) 列到达,所以本题解题思路就来了。
dp四步法:
-
确定状态
dp[i][j]表示 \((i,j)\) 能或得到的最大数字之和。 -
确定答案
max{dp[i][1]~dp[i][m]}中的最大值。 -
确定状态转移方程
dp[i][j][0] = max(dp[i-1][j][0], max(dp[i][j-1][1], dp[i][j-1][0])) + a[i][j]; dp[i][j][1] = max(dp[i+1][j][1], max(dp[i][j-1][1], dp[i][j-1][0])) + a[i][j];注意:
以上两个的方程要列不同的
for循环,反正我又不给代码。拓展知识我就不做了,因为我善。
-
确定初始状态和边界
把
dp数组全部都复制为LONGLONG_MIN。第一列要初始化,所以还要跑一边循环。
D1238 【例9.11】01背包问题暨01背包问题讲解
当我们开始学这道题的时候,就代表我们开始学01背包了。
但是为了水字数巩固知识点,我先把01背包给讲一下。
01背包理论知识
从名字上就很好理解, \(0\) 代表不选, \(1\) 代表选。
同时对应着dfs中的选和不选问题(驭澄音)。
这种问题一般有3种写法:
- 第一种就是最简单并且本人最会的暴搜,只要数据不大,优势在我。
- 第二种就是本人最不会的贪心。这里的贪心可贪多个值
,比何坤还能贪。 - (第三种写法在后面)。
接下来我们要用贪心的角度想一下这道题:
-
按照重量贪。
容量10
物品1 物品2 物品三 重量 10 6 4 价值 1 0.1 0.1 重量贪:物品2+物品3=0.1+0.1=2
正常:物品1=10
直接过
-
按照价格贪。
容量10
物品1 物品2 物品三 重量 10 6 4 价值 10 8 4 价格贪:物品1=10
正常:物品2+物品3=8+4=12
也过
-
按照性价比贪。
容量10
物品1 物品2 物品三 重量 8 6 4 价值 10 7 4 性价比 1.25 0.86 1 性价比贪:物品1=10
正常:物品2+物品3=7+4=11
也过
看得出来,贪心的每一个方法都有hack。
不藏了,我们现在直接拿出我们的dp吧。
温馨提示:
01背包属于多状态
dp。 时间复杂度: \(O(n*m)\)
空间复杂度: \(O(n*m)\)
解题
这题给定一个容量为 \(m\) 的背包,现在有 \(n\) 件物品,每件物品只有一个,问从中任意挑选装入到背包
之中可以获取的最大价值。
-
确定状态:
dp[i][j]代表着前面 \(i\) 件商品,任意挑选装入到背包容量为 \(j\) 的背包之中可以获取到的最大价值。\(j\) 是背包的容量,背包可以不装满。
-
确定答案
dp[n][m] max{dp[1][m]~dp[i][m]} 以上两种都是对的。 这个题目的答案存在单调性,物品数量越多,挑选的自由度越高,答案是非下降的 -
确定状态转移方程
第一种
第i件物品准备装入
分两种情况
装得下:
dp[i-1][j-w[i]]+val[i] 装不下:
dp[i-1][j]第二种
第i件物品不准备装入
dp[i - 1][j]合并之后发现,只有装得下和装不下两种情况。
所以代码如下:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + val[i]); //装入第i件物品和不装入第i件物品做选择 ff(i, 1, n)ff(j, 0, w)if (j >= w[i]) //装得下,所以有两种选择dp[i][j] = max(dp[i - 1][jl, dp[i - 1][j - w[i]] + val{i]) ;elsedp[i][j] = dp[i - 1][j]; //装不下不装入 -
确定初始状态和边界
dp[0][0]=0;//不选任何物品放入到容量为0的背包之中,答案就是0 (真实存在) dp[i][0]=0;//选择前i件物品放入到容量为0的背包之中,答案就是0(真实存在) dp[0][j]=0; //选择前0件物品放入到背包容量为j的背包之中,答案是0(实际不存在的)
D1253 Charm Bracelet
这题就是D1238 【例9.11】01背包问题的数据加强版。
这题只需要把dp改成一维数组,然后在用个pre数组存储上一次的答案按就可以了,没啥好说的。
P1802 5 倍经验日
这题也跟D1253 Charm Bracelet一样,都是拿这个D1238 【例9.11】01背包问题模板题改的。
这题主要是long long的问题和失败也加分,其他的也都没有了。