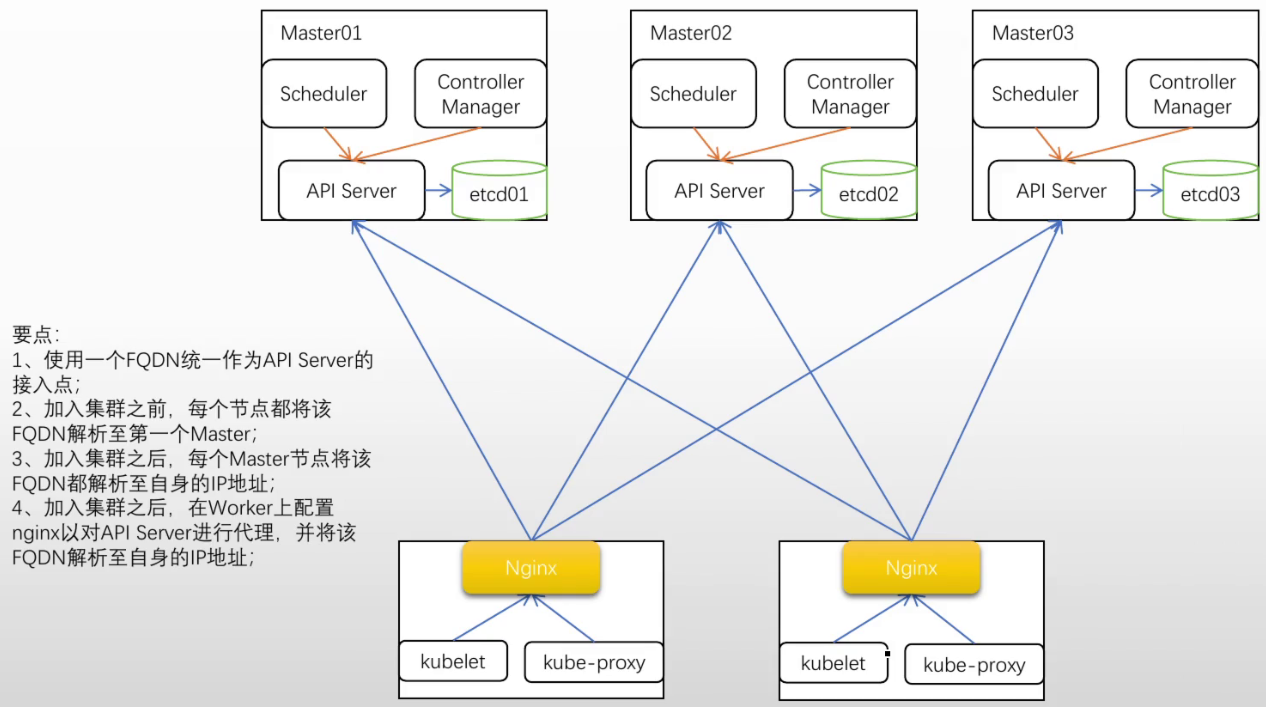
1. 基本概念
1.1 流网络,不考虑反向边

如果存在反向边也没事,不如有u->v和v->u两条边,那么就可以新加入一个点 p,u->v,v->p,p->u,转化为这三条边
1.2 可行流,不考虑反向边
1.2.1 两个条件:容量限制、流量守恒
容量限制:每条边流的不能超过这条边的权值
流量守恒:每个点流入的流量等于流出去的流量()

1.2.2 可行流的流量指从源点流出的流量 - 流入源点的流量
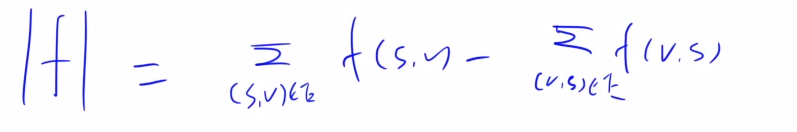
1.2.3 最大流是指最大可行流
1.3 残留网络,考虑反向边,残留网络的可行流f' + 原图的可行流f = 原题的另一个可行流
(1) |f' + f| = |f'| + |f|
(2) |f'| 可能是负数
1.4 增广路径
1.5 割1.5.1 割的定义1.5.2 割的容量,不考虑反向边,“最小割”是指容量最小的割。1.5.3 割的流量,考虑反向边,f(S, T) <= c(S, T)1.5.4 对于任意可行流f,任意割[S, T],|f| = f(S, T)1.5.5 对于任意可行流f,任意割[S, T],|f| <= c(S, T)1.5.6 最大流最小割定理(1) 可行流f是最大流(2) 可行流f的残留网络中不存在增广路(3) 存在某个割[S, T],|f| = c(S, T)
1.6. 算法1.6.1 EK O(nm^2)1.6.2 Dinic O(n^2m)
1.7 应用1.7.1 二分图(1) 二分图匹配(2) 二分图多重匹配1.7.2 上下界网络流(1) 无源汇上下界可行流(2) 有源汇上下界最大流(3) 有源汇上下界最小流1.7.3 多源汇最大流