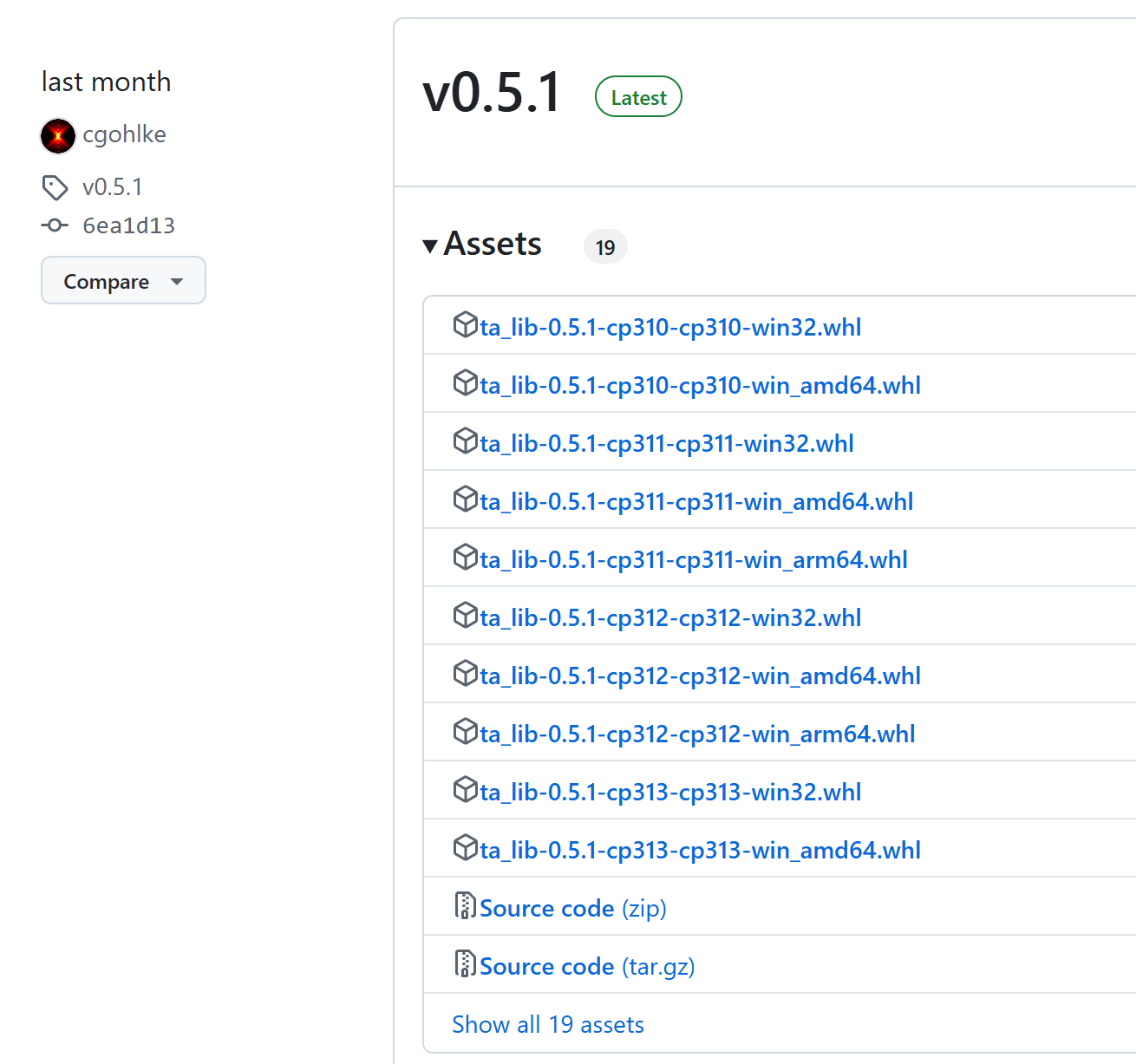
根据加速定理,我们明白了我们必须对算法定义复杂性而不能对问题定义复杂性。然而,直观上确实存在不同问题的难易程度(hardness)之分。有的问题只需要扫描一遍输入就可以求出,有的问题似乎除了暴力搜索之外没有好办法。那么我们应该如何比较不同问题之间的难度呢?(除非特殊说明,我们所说的“问题”就是指判定性问题,一个问题\(L\)是\(\{0,1\}^\ast\)的一个子集)
归约
\(m\)-归约
\(\newcommand{\M}{\mathbb{M}}\)比较问题难度的最直接也是最本质的方法就是归约(reduction)。当我们要判定一个问题\(A\)时,如果我们能找到一个可计算全函数\(f\)使得\(x\in A\iff f(x)\in B\),那么我们就可以对于每个输入\(x\)做一步计算\(f(x)\)而把问题转化为\(B\)。如果这样的\(f\)存在,我们就称问题\(A\)能归约成问题\(B\)。这是最基本的归约形式,称为\(m\)-归约,记为\(A\leq_mB\)。如果\(A\leq_m B\),则说明只要我们有办法解决\(B\)就一定能解决\(A\),所以\(B\)是一个比\(A\)难或至少\(A\)不比\(B\)更难。
\(m\)-归约和我们直观上理解的“归约”还是有一些差距的。我们从图灵机的角度看\(m\)-归约,它说的实际上是:如果存在一个判定\(B\)的图灵机\(\M_B\),存在一个计算\(f\)的图灵机\(\M_f\),那么我们可以构造一台判定\(A\)的图灵机\(\M_A\),方法是对于每个输入\(x\),先调用子程序\(\M_f\)计算得到\(f(x)\),在把\(f(x)\)作为\(\M_B\)的输入,那么\(\M_B\)的输出刚好就是判定\(x\in A\)的正确答案。注意到在这个过程中,我们只允许\(\M_A\)调用一次子程序\(\M_B\),并且必须是在程序末尾调用。而在我们直观上理解的“归约”中,我们应当可以反复调用\(\M_B\)多次,并且不一定是在结尾时调用。
图灵归约
为了让归约的定义更加直观,我们引入神谕图灵机(oracle Turing machine)的概念。一台带有问题\(L\)的神谕图灵机可以在运行过程中用一步计算的代价询问是否有\(x\in L\)并获得正确回答(因此,这也是一个假想模型)。具体的,定义神谕图灵机\(\M^L\)上有一条神谕带,它有三个额外的运行状态\(q_{query},q_{yes},q_{no}\),某时刻如果神谕带上写着\(z\),并且图灵机进入状态\(q_{query}\),那么下一步如果\(z\in L\)就会进入状态\(q_{yes}\),否则就会进入状态\(q_{no}\)。
如果存在一台神谕图灵机\(\M^B\)使得\(\M^B\)能够判定问题\(A\),就称\(A\)能图灵归约到\(B\),记为\(A\leq_T B\)。由此可见,图灵归约可以反复调用判定\(B\)的子程序,并且可以在调用的间隙做计算。这符合我们对归约的直观印象。
多项式归约
在复杂性中,我们特别关心多项式时间可完成的归约(高效归约)。
和\(m\)-归约对应,我们定义Karp归约:如果存在一个多项式时间可计算全函数\(f\)使得\(x\in A\iff f(x)\in B\),那么就称问题\(A\)能Karp归约为问题\(B\)。记为\(A\leq_K B\)。
和图灵归约对应,我们定义Cook归约:如果存在一台多项式运行时间的神谕图灵机\(\M_P^B\)使得\(\M_P^B\)能够判定问题\(A\),就称\(A\)能Cook归约到\(B\),记为\(A\leq_C B\)。(如果我们定义复杂性类\(\text{P}^L\)为所有带神谕\(L\)的多项式时间图灵机能判定的问题集合,那么“存在一台多项式运行时间的神谕图灵机\(\M_P^B\)使得\(\M_P^B\)能够判定问题\(A\)”可以写为\(A\in \text{P}^B\))
显然,归约有传递性。因此我们可以良好的比较问题间的大小。比较的方式可以是\(m\)-归约,也可以是图灵归约、多项式归约。不同的比较方法会导致不同的难易指标。
时间意义的难度
在时间复杂性中,研究\(\text{P}\)是否等于\(\text{NP}\)时,我们可以采取这样的思路:如果在多项式归约意义下\(\text{NP}\)中最难的那个问题能被多项式解决,那么我们也就证明了\(\text{P}=\text{NP}\)。
如果存在问题\(B\)使得\(\forall A\in \text{NP}\),\(A\leq_K B\),那么就称\(B\)是一个NP-hard问题(注意这里我们用的是Karp归约,也即只能调用一次子程序的多项式归约)。如果\(BL\)是NP-hard的并且\(B\in \text{NP}\),那么就称\(B\)是NP-complete的。定义问题类\(\text{NPC}\)是所有NP-complete问题的集合。
Cook-Levin定理指出,SAT问题是NP-complete的。证明:证毕。
Karp证明了SAT问题可以Karp归约到21个组合问题,包括3SAT、图的点覆盖问题、01整数规划等等耳熟能详的问题。只要证明这些问题中的任何一个有多项式算法,就能证明\(\text{P}=\text{NP}\)。
一个有趣的问题是,如果\(\text{P}\neq\text{NP}\),那么\(\text{NP}\setminus\text{P}\)中是否含有除了NP-complete问题以外的其它问题?Ladner定理指出,\(\text{NP}\setminus\text{P}\)中确实含有除了NP-complete问题以外的其它问题,并且这样的问题数量是无穷多的。证明:证毕。
空间意义的难度
类比时间复杂性,在那里我们可以用最小的时间资源类\(\text{P}\)来定义归约,从而能够比较不同问题在时间复杂性意义下的难度。那么对于空间复杂性,我们能否用最小的空间资源类\(\text{L}\)来定义归约,从而比较不同问题在空间复杂性意义下的难度呢?
如果存在一个对数空间可计算的全函数\(f\)使得\(x\in A\iff f(x)\in B\),那么就称问题\(A\)能对数空间归约为问题\(B\)。记为\(A\leq_L B\)。
以上定义等价于:如果存在一个隐式对数空间可计算(implicitly logspace computable)全函数\(f\)使得\(x\in A\iff f(x)\in B\),那么就称问题\(A\)能对数空间归约为问题\(B\)。记为\(A\leq_L B\)。其中,\(f\)是隐式对数空间可计算的当且仅当 ①\(\forall x,|f(x)|\)是关于\(|x|\)的多项式长的;②输入\(x,i\),判定是否成立\(i\leq |f(x)|\)的问题只需要对数空间;③输入\(x,i\),判定是否成立\(f(x)\)的第\(i\)位是1只需要对数空间。这三点定义“隐式地”保证了\(f\)的计算只需要用到对数空间,因为对于每个\(x\),计算\(f(x)\)的每一位以及计算\(f(x)\)的位数都只需要对数空间。
如果存在问题\(B\)使得\(\forall A\in \text{L}\),\(A\leq_L B\),那么就称\(B\)是一个L-hard问题。如果\(B\)是L-hard的并且\(B\in \text{L}\),那么就称\(B\)是L-complete的。类似的,可以定义NL-hard,NL-complete,PSPACE-hard,PSPACE-complete等等(都是用对数空间归约定义)。
可达性问题(Reachability Problem)是指:给定一张有向图和有向图上两个节点,判定两点间是否存在一条可达路径。可以证明,可达性问题是NL-complete问题,也即所有非确定性图灵机能在对数空间判定的问题都可以归约为可达性问题,并且可达性问题本身也只需要非确定性图灵机在对数空间内判定。
量化布尔公式问题(Quantified Boolean Formula Problem, QBF Problem)是指:。Stockmeyer-Meyer定理指出,QBF问题是PSPACE-complete的。
Savitch定理指出:对于空间可构造函数\(S(n)\),始终成立\(\text{NSPACE}(S(n))\subseteq \text{SPACE}((S(n))^2)\)。也即非确定性图灵机在空间\(S(n)\)下能判定的问题一定能用确定性图灵机在\(S(n)^2\)的空间内判定。这里的平方使得我们能把多项式空间的确定性图灵机和多项式空间的非确定性图灵机等价起来。当我们要证明一个问题可以用确定性图灵机在多项式空间内判定时,只需证明这个问题可以用非确定性图灵机在多项式空间内判定。这意味着\(\text{PSPACE}=\text{NPSPACE}\)。这是一个有点反直觉的结论,侧面反映出多项式空间类已经是一个极其广大的类了。
根据Savitch定理,设\(\text{NPSPACE}\)在全集\(\{0,1\}^*\)下的补集