Shor’s Algorithm

本文延续RSA与ECC-ElGamal。

Shor算法（Shor’s Algorithm）几乎是最为出名的量子算法，原因就在于其可以在多项式的时间复杂度内完成大数的质因分解问题。也由此，基于质因分解难题的RSA算法受到了严重的量子威胁，而RSA算法正是在日常生活之中最为常用（如HTTPS协议、SSH协议、X.509证书等）的非对称算法。
事实上对于Shor算法，其更为广义的用法是求解离散对数问题（Discrete Logarithm Problem，DLP）。类似于RSA算法，SM2算法、ECDHE算法等其安全性则是基于椭圆曲线离散对数问题（Elliptic Curve Discrete Logarithm Problem，ECDLP），同样受到了Shor算法的威胁。
注：关于经典环境中关于ECDLP问题的小子群攻击思想可以参考ECDLP。
下文将对如何在量子环境中利用Shor算法攻击RSA算法（DLP）以及基于椭圆曲线的算法（ECDLP）做简要介绍及分析。

一些基础
（本节对于熟悉RSA算法机制或是群论的可以跳过）
观察如下周期函数：

\(f(x)=a^x\mod{N}\)

• 注解：模及模运算
  模运算（简写为\(\mbox{mod}\)）表示一个数除以另一个数的与余数，如：\(17\mod{5}=2\)
  因为\(17÷5=3\)有余数\(2\)（即，\(17=(3×5)+2\)）。在Python中，模运算的符号记为%。
  从而，对应的模运算即为\(12\equiv 2(\mod{5})\)
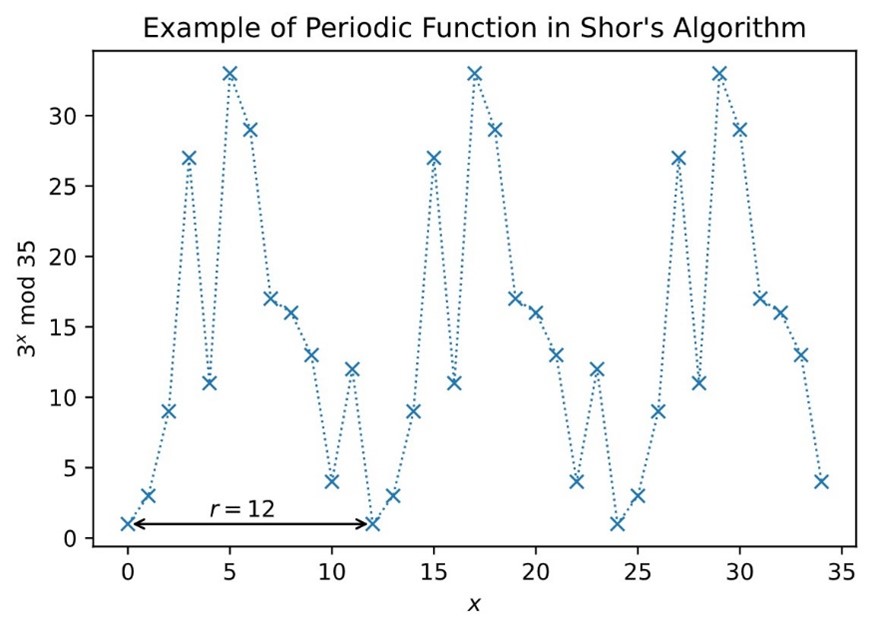
  其中，\(a\)和\(N\)为正整数，\(a\)小于\(N\)，且二者没有相同的因数。周期，或者说阶（\(r\)），是满足下式的最小（非零）整数：\(a^r\mod{N}=1\)

下图展示了上述模运算的图像。要注意，点之间的连线仅是为了方便观察周期性，并不表示连线之间具有实际含义的取值。

Shor算法的实现
Shor算法使用类似于量子相位估计算法（Quantum Phase Estimation，QPE）的酉算子：

\(U|y〉≡|ay\mod{N}〉\)
为了深入理解算子\(U\)的含义，需要寻找其对应的特征值（此处不妨回想一下线性代数之中，\(U\)算子即为一个矩阵，而量子态\(|y〉\)则为一个列向量，因为量子算法中的算子均符合幺正性，则对于一个量子态必然会有一个特征值）。若从量子态\(|1〉\)开始，可以看到每次对其应用\(U\)算子都是相当于进行了一次乘\(a\)的模运算。当应用\(r\)次之后，量子态回到了开始的量子态\(|1〉\)。例如，当\(a=3\)且\(N=35\)时：\(U|1〉=|3〉\)
\(U^2 |1〉=|9〉\)
\(U^3 |1〉=|27〉\)
\(⋮\)
\(U^{(r-1)}|1〉=|12〉\)
\(U^r |1〉=|1〉\)

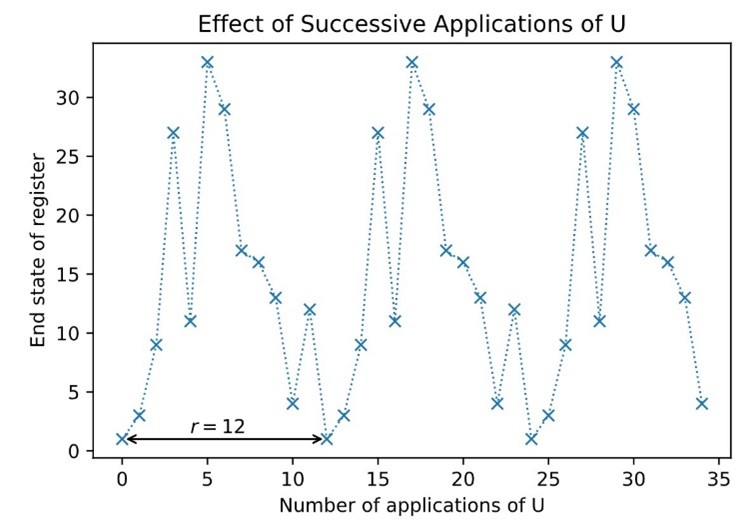
如此，考虑如下其本征态是循环的叠加态\(|u_0〉\)，及其应用\(U\)算子时的特征值：

\(|u_0〉=\frac{1}{\sqrt{r}} \sum\limits_{k = 0}^{r - 1} e^{\frac{-2πik}{r}}|a^k\mod{N}〉\)
\(U|u_1 〉=e^{\frac{2πi}{r}}|u_1 〉\)

• 例如，当\(a=3\)且\(N=35\)时：\(\left| u_{1} \right\rangle = \frac{1}{\sqrt{12}}\left( {\left| 1 \right\rangle + e^{- \frac{2\pi i}{12}}\left| 3 \right\rangle + e^{- \frac{4\pi i}{12}}\left| 9 \right\rangle\cdots + e^{- \frac{20\pi i}{12}}\left| 4 \right\rangle + e^{- \frac{22\pi i}{12}}\left| 12 \right\rangle} \right)\)\(U\left| u_{1} \right\rangle = \frac{1}{\sqrt{12}}\left( {\left| 3 \right\rangle + e^{- \frac{2\pi i}{12}}\left| 9 \right\rangle + e^{- \frac{4\pi i}{12}}\left| 27 \right\rangle\cdots + e^{- \frac{20\pi i}{12}}\left| 12 \right\rangle + e^{- \frac{22\pi i}{12}}\left| 1 \right\rangle} \right)\)\(U\left| u_{1} \right\rangle = e^{\frac{2\pi i}{12}} \cdot \frac{1}{\sqrt{12}}\left( {e^{- \frac{2\pi i}{12}}\left| 3 \right\rangle + e^{- \frac{4\pi i}{12}}\left| 9 \right\rangle + e^{- \frac{6\pi i}{12}}\left| 27 \right\rangle\cdots + e^{- \frac{22\pi i}{12}}\left| 12 \right\rangle + e^{- \frac{24\pi i}{12}}\left| 1 \right\rangle} \right)\)\(U\left| u_{1} \right\rangle = e^{\frac{2\pi i}{12}}\left| u_{1} \right\rangle\)此处可以看到\(r=12\)出现在了量子态相位指数的分母。

这个特征值（即\(e^\frac{2πi}{r}\)）非常重要，因为其包含了周期\(r\)。事实上，\(r\)必须出现在此处，从而确保\(r\)计算基态（\(r\) computational basis states）的相位差相等。上述的量子态\(|u_1 〉\)并不是唯一具有这种特性的特征态。为了更具一般性，考虑如下的量子态：

\(\left| u_{s} \right\rangle = \frac{1}{\sqrt{r}}{\sum\limits_{k = 0}^{r - 1}{e^{- \frac{2\pi isk}{r}}\left| {a^{k}~\text{mod}~N} \right\rangle}}\)
\( U\left| u_{s} \right\rangle = e^{\frac{2\pi is}{r}}\left| u_{s} \right\rangle\)

• 例如，当\(a=3\)且\(N=35\)时：\(\left| u_{s} \right\rangle = \frac{1}{\sqrt{12}}\left( {\left| 1 \right\rangle + e^{- \frac{2\pi is}{12}}\left| 3 \right\rangle + e^{- \frac{4\pi is}{12}}\left| 9 \right\rangle\cdots + e^{- \frac{20\pi is}{12}}\left| 4 \right\rangle + e^{- \frac{22\pi is}{12}}\left| 12 \right\rangle} \right)\)\(U\left| u_{s} \right\rangle = \frac{1}{\sqrt{12}}\left( {\left| 3 \right\rangle + e^{- \frac{2\pi is}{12}}\left| 9 \right\rangle + e^{- \frac{4\pi is}{12}}\left| 27 \right\rangle\cdots + e^{- \frac{20\pi is}{12}}\left| 12 \right\rangle + e^{- \frac{22\pi is}{12}}\left| 1 \right\rangle} \right)\)\( U\left| u_{s} \right\rangle = e^{\frac{2\pi is}{12}} \cdot \frac{1}{\sqrt{12}}\left( {e^{- \frac{2\pi is}{12}}\left| 3 \right\rangle + e^{- \frac{4\pi is}{12}}\left| 9 \right\rangle + e^{- \frac{6\pi is}{12}}\left| 27 \right\rangle\cdots + e^{- \frac{22\pi is}{12}}\left| 12 \right\rangle + e^{- \frac{24\pi is}{12}}\left| 1 \right\rangle} \right)\)\(U\left| u_{s} \right\rangle = e^{\frac{2\pi is}{12}}\left| u_{s} \right\rangle\)

现在，对于\(s\)的每个取值都有了一个对应的特征值，其中

$0≤s≤r-1$ 事实上若是将这些量子态求和，除了$|1〉$之外的本征态的相位将会相互抵消，从而有： $ \frac{1}{\sqrt{r}}{\sum\limits_{s = 0}^{r - 1}\left| u_{s} \right\rangle} = \left| 1 \right\rangle$

• 例如，当\(a=7\)且\(N=15\)时(有\(r=4\))：\( \begin{matrix} \frac{1}{2} & ( & {\left| u_{0} \right\rangle = \frac{1}{2}\left( \left| 1 \right\rangle \right.} & + & \left| 7 \right\rangle & + & \left| 4 \right\rangle & + & \left. \left| 13 \right\rangle \right) & \cdots & ~ \\ ~ & + & {\left| u_{1} \right\rangle = \frac{1}{2}\left( \left| 1 \right\rangle \right.} & {+ e^{- \frac{2\pi i}{4}}} & \left| 7 \right\rangle & {+ e^{- \frac{4\pi i}{4}}} & \left| 4 \right\rangle & {+ e^{- \frac{6\pi i}{4}}} & \left. \left| 13 \right\rangle \right) & \cdots & ~ \\ ~ & + & {\left| u_{2} \right\rangle = \frac{1}{2}\left( \left| 1 \right\rangle \right.} & {+ e^{- \frac{4\pi i}{4}}} & \left| 7 \right\rangle & {+ e^{- \frac{8\pi i}{4}}} & \left| 4 \right\rangle & {+ e^{- \frac{12\pi i}{4}}} & \left. \left| 13 \right\rangle \right) & \cdots & ~ \\ ~ & + & {\left| u_{3} \right\rangle = \frac{1}{2}\left( \left| 1 \right\rangle \right.} & {+ e^{- \frac{6\pi i}{4}}} & \left| 7 \right\rangle & {+ e^{- \frac{12\pi i}{4}}} & \left| 4 \right\rangle & {+ e^{- \frac{18\pi i}{4}}} & \left. \left| 13 \right\rangle \right) & ) & {= \left| 1 \right\rangle} \end{matrix}\)

由于基态\(|1〉\)是上述量子态的叠加态，这也意味着若是对基态\(|1〉\)应用带\(U\)算子的\(QPE\)，将会测得相位为：

$\phi = \frac{s}{r}$ 其中，$s$是一个介于$0$至$r-1$之间的整数。最后，可以利用$ϕ$的[连分数算法](https://en.wikipedia.org/wiki/Continued_fraction)来计算$r$。

应用于RSA算法
本节不再对RSA算法进行介绍，原理参阅RSA。
应用于RSA算法的Shor算法量子线路图如下：

注意：量子线路图中的上方为低位量子比特，下方为高位量子比特。此外，为了方便叙述，此节之后不再记函数的周期为\(r\)而为\(R\)，且重记\(⌈r⌉=\log_{2}⁡R\)，上述量子图中\(r\)仍指函数周期。

1. 算法开始时，初始化低位的\(n\)个量子比特为\(|0〉\)且初始高位\(r\)个量子比特为\(|1〉\)。之后，对低位应用\(QFT\)算子（Quantum Fourier Transform，量子傅里叶变换。注：在对零态\(|0〉\)应用\(QFT\)算子时与\(Hadamard\)变换\(H^{⨂n}\)等效。），此时的量子态为：\(\left| 0 \right\rangle\left| 1 \right\rangle\overset{QFT}{\rightarrow}\frac{1}{\sqrt{N}}{\sum\limits_{k = 0}^{N - 1}\left| k \right\rangle}\left| 1 \right\rangle = \frac{1}{\sqrt{N}}{\sum\limits_{k = 0}^{N - 1}\left| k \right\rangle}\frac{1}{\sqrt{R}}{\sum\limits_{s = 0}^{R - 1}\left| u_{s} \right\rangle} = \frac{1}{\sqrt{NR}}{\sum\limits_{k = 0}^{N - 1}{\sum\limits_{s = 0}^{R - 1}{\left| k \right\rangle\left| u_{s} \right\rangle}}}\)其中，\(N=2^n\)。
2. 之后，以低位量子比特为控制位对高位应用受控\(U^k\)算子，获得量子态为：\(\begin{matrix} {\frac{1}{\sqrt{NR}}{\sum\limits_{k = 0}^{N - 1}{\sum\limits_{s = 0}^{R - 1}{\left| k \right\rangle U^{k}\left| u_{s} \right\rangle}}}} & = & {\frac{1}{\sqrt{NR}}{\sum\limits_{k = 0}^{N - 1}{\sum\limits_{s = 0}^{R - 1}{\left| k \right\rangle e^{\frac{2\pi iks}{R}}\left| u_{s} \right\rangle}}}} \\ & = & {\frac{1}{\sqrt{R}}{\sum\limits_{s = 0}^{R - 1}{\frac{1}{\sqrt{N}}{\sum\limits_{k = 0}^{N - 1}{e^{\frac{2\pi iks}{R}}\left| k \right\rangle}}\left| u_{s} \right\rangle}}} \\ & = & {\frac{1}{\sqrt{R}}{\sum\limits_{s = 0}^{R - 1}{\left| {\mathcal{S}_{N}\left( {s/R} \right)} \right\rangle\left| u_{s} \right\rangle}}} \end{matrix}\)其中，\( \left| {\mathcal{S}_{N}\left( {s/R} \right)} \right\rangle = e^{\frac{2\pi iks}{R}}\left| k \right\rangle\)。
   注：对任意量子态应用\(QFT\)算子的结果为\(QFT\left| x \right\rangle = \frac{1}{\sqrt{n}}{\sum\limits_{y = 0}^{n - 1}{e^{\frac{2\pi iyx}{n}}\left| y \right\rangle}} = \left| {\mathcal{S}_{n}\left( {x/n} \right)} \right\rangle\)。
3. 最后，对低位应用\({QFT}^{\dagger}\)算子（即逆\(QFT\)算子），获得量子态为：\(\frac{1}{\sqrt{R}}{\sum\limits_{s = 0}^{R - 1}{\left| \frac{sN}{R} \right\rangle\left| u_{s} \right\rangle}} = \frac{1}{\sqrt{R}}{\sum\limits_{s = 0}^{R - 1}{\left| {\frac{N}{R} \cdot s} \right\rangle\left| u_{s} \right\rangle}}\)其中，\(N\)为常数且低位量子比特与高位量子比特处于纠缠态。此时，若对高位量子比特进行测量，则会以均等的概率从\(F_R\)中获得一个确定的\(s\)，同时低位量子比特量子态中的\(s\)则被确定，进而对低量子比特进行测量可以确定性地获得\(R\)的值。

综上，Shor算法的量子态的整体量子表述为：

$\begin{array}{lll} {\left| 0 \right\rangle\left| 1 \right\rangle} & \overset{QFT}{\rightarrow} & {\frac{1}{\sqrt{N}}{\sum\limits_{k = 0}^{N - 1}\left| k \right\rangle}\left| 1 \right\rangle = \frac{1}{\sqrt{N}}{\sum\limits_{k = 0}^{N - 1}\left| k \right\rangle}\frac{1}{\sqrt{R}}{\sum\limits_{s = 0}^{R - 1}\left| u_{s} \right\rangle} = \frac{1}{\sqrt{NR}}{\sum\limits_{k = 0}^{N - 1}{\sum\limits_{s = 0}^{R - 1}{\left| k \right\rangle\left| u_{s} \right\rangle}}}} \\& \overset{U^{k}}{\rightarrow} & \begin{array}{lll} {\frac{1}{\sqrt{NR}}{\sum\limits_{k = 0}^{N - 1}{\sum\limits_{s = 0}^{R - 1}{\left| k \right\rangle U^{k}\left| u_{s} \right\rangle}}}} & = & {\frac{1}{\sqrt{NR}}{\sum\limits_{k = 0}^{N - 1}{\sum\limits_{s = 0}^{R - 1}{\left| k \right\rangle e^{\frac{2\pi iks}{R}}\left| u_{s} \right\rangle}}}} \\& = & {\frac{1}{\sqrt{R}}{\sum\limits_{s = 0}^{R - 1}{\frac{1}{\sqrt{N}}{\sum\limits_{k = 0}^{N - 1}{e^{\frac{2\pi iks}{R}}\left| k \right\rangle}}\left| u_{s} \right\rangle}}} \\& = & {\frac{1}{\sqrt{R}}{\sum\limits_{s = 0}^{R - 1}{\left| {\mathcal{S}_{N}\left( {s/R} \right)} \right\rangle\left| u_{s} \right\rangle}}} \end{array} \\& \overset{{QFT}^{\dagger}}{\rightarrow} & {\frac{1}{\sqrt{R}}{\sum\limits_{s = 0}^{R - 1}{\left| \frac{sN}{R} \right\rangle\left| u_{s} \right\rangle}} = \frac{1}{\sqrt{R}}{\sum\limits_{s = 0}^{R - 1}{\left| {\frac{N}{R} \cdot s} \right\rangle\left| u_{s} \right\rangle}}} \end{array}$

通过Shor算法破解RSA算法可以从两方面入手，其一是公开的大整数\(n_r=p_r×q_r\)，其二可以是密文\(c_r\)。
注：此处采用RSA中的符号，为了与Shor算法的符号做出区分，RSA算法的符号均包含下标\(r\)。

1、大整数\(n_r\)
考虑大整数\(n_r=p_r×q_r\)，其欧拉函数为\(φ⁡(n_r)\)，由欧拉定理显然有

$\left. r_{r} = {\varphi\left( n_{r} \right)}\Leftrightarrow a^{r_{r}} \equiv 1~\left( {\text{mod}~n_{r}} \right) \right.$ 其中，$a∈F_{n_r}$。此时便可以通过Shor算法，将$r_r=φ⁡(n_r)$求解出来，又因为对于RSA算法有 $d_{r} \cdot e_{r} \equiv 1~\left( {\text{mod}~{\varphi\left( n_{r} \right)}} \right)$ 其中$e_r$是RSA算法公开的公钥，则私钥$d_r$就是$e_r$对于的乘法逆元。考虑Shor算法的在量子线路中运行的时间复杂度是多项式时间，则上述过程表明了RSA算法在量子环境中仅有多项式级的安全性。 此外，注意本部分的开始的等式$r_r=φ⁡(n_r)$，此处事实上存在如下关系： $a^{r_{r}} - 1 \equiv 0~\left( {mod~n} \right)$ $\left. \Rightarrow\left( {a^{r_{r}/2} - 1} \right)\left( {a^{r_{r}/2} + 1} \right) \equiv 0~\left( {mod~n} \right) \right.$ $\left. \Rightarrow\left\{ \begin{matrix} {{\gcd\left( {\left( {a^{r_{r}/2} - 1} \right),n} \right)} = p_{r}} \\ {{\gcd\left( {\left( {a^{r_{r}/2} + 1} \right),n} \right)} = q_{r}} \end{matrix} \right. \right.$ 上述的过程便通过Shor算法实现了对大整数$n_r$的因式分解。

2、密文\(c_r\)
对于密文\(c_r\)，不难注意到

${c_{r}}^{r_{r}} = {c_{r}}^{\varphi{(n_{r})}} \equiv 1~\left( {\text{mod}~n_{r}} \right)$ 如此，便可以对密文使用Shor算法，从而获得$φ⁡(n_r)$对应的值。类似上述1过程，由于 $d_{r} \cdot e_{r} \equiv 1~\left( {\text{mod}~{\varphi\left( n_{r} \right)}} \right)$

应用于椭圆曲线
此处不对如双线性对这样的复杂椭圆曲线加密机制进行深入，仅考虑如ECC-ElGamal这样的相对简单的机制。
对于基于椭圆曲线的公钥加密算法（ECC）应用Shor算法需要对其进行一定的修改，量子线路图如下所示

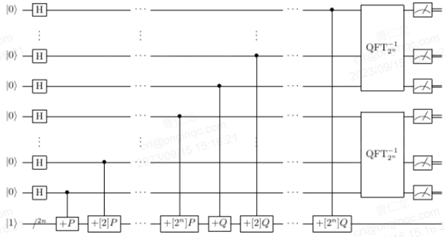
不难看出，与应用于RSA算法的量子线路区别主要有两点。

1. 低量子比特位的控制位由之前的一组\(n\)个量子比特变为了两组共\(2n\)个量子比特。
2. \(U^k\)算子的运算变为了椭圆曲线上的倍点运算，即“\(+[k]P\)”和“\(+[k]Q\)”。

在应用至ECC之前，首先对上述量子线路的量子态变化进行分析，不难得到如下公式

$ \begin{array}{lll} {\left| 0 \right\rangle\left| 0 \right\rangle\left| 1 \right\rangle} & \overset{QFT}{\rightarrow} & {\frac{1}{\sqrt{N}}{\sum\limits_{x}\left| x \right\rangle}\frac{1}{\sqrt{N}}{\sum\limits_{y}\left| y \right\rangle}\frac{1}{\sqrt{R}}{\sum\limits_{s}\left| u_{s} \right\rangle}} \\& \overset{U^{k}}{\rightarrow} & \begin{array}{lll} {\frac{1}{N\sqrt{R}}{\sum\limits_{x,y,s}{\left| x \right\rangle\left| y \right\rangle U_{Q}^{y}U_{P}^{x}\left| u_{s} \right\rangle}}} & = & {\frac{1}{N\sqrt{R}}{\sum\limits_{x,y,s}{\left| x \right\rangle\left| y \right\rangle U_{G}^{ax + by}\left| u_{s} \right\rangle}}} \\& = & {\frac{1}{N\sqrt{R}}{\sum\limits_{x,y,s}{\left| x \right\rangle\left| y \right\rangle e^{\frac{2\pi is{({ax + by})}}{R}}\left| u_{s} \right\rangle}}} \\& = & {\frac{1}{\sqrt{R}}{\sum\limits_{s}{\left( {{\sum\limits_{x}{e^{\frac{2\pi isax}{R}}\left| x \right\rangle}}\bigotimes{\sum\limits_{y}{e^{\frac{2\pi isby}{R}}\left| y \right\rangle}}} \right)\left| u_{s} \right\rangle}}} \\& = & {\frac{1}{\sqrt{R}}{\sum\limits_{s}{\left( {\left| {\mathcal{S}_{N}\left( {{as}/R} \right)} \right\rangle\bigotimes\left| {\mathcal{S}_{N}\left( {{bs}/R} \right)} \right\rangle} \right)\left| u_{s} \right\rangle}}} \end{array} \\& \overset{{QFT}^{\dagger}}{\rightarrow} & {\frac{1}{\sqrt{R}}{\sum\limits_{s}{\left( {\left| {\frac{N}{R} \cdot as} \right\rangle\bigotimes\left| {\frac{N}{R} \cdot bs} \right\rangle} \right)\left| u_{s} \right\rangle}}} \end{array} $其中，$a,b∈\mathbb{F}_R$，$R=♯⁡E$表示曲线上点的数量（当$♯⁡E$不为素数时随着$G$的选取，可能会有$R≠♯⁡E$，此时$R$为以$G$为基点进行倍点运算所形成的加法群的阶），$G$表示ECC的基点，不失一般性的可以认为$P=[a]G$且$Q=[b]G$，$U_G^x$表示$+[x]G$运算，进而有$U_P^x=U_G^{ax}$且$U_Q^y=U_G^{by}$，类似地有$U_G^x |u_s 〉=e^{\frac{2πisx}{R}} |u_s 〉$。此时，由于$N$为已知常数，$R$为ECC公开常数，$s$由于高低位量子比特处于纠缠态故有相同的值，所以对低位量子比特进行测量可以获得依次获得$as$与$bs$的值，即$\frac{as}{bs}=\frac{a}{b}$。

考虑如ECC-ElGamal的加密机制，公钥\(Y=[x]G\)、基点\(G\)均为公开，其中\(x\)为私钥。此时，便可以令\(P=Y=[x]G\)、\(Q=G\)，即有\(a=x\)、\(b=1\)。进而，经过上述Shor算法的运算后即可获得比值\(\frac{a}{b}=\frac{x}{1}=x\)，如此便在多项式的时间内破解了基于椭圆曲线的非对称加密算法。

至此，便实现了在量子环境下利用Shor算法在多项式的时间复杂度内对基于DLP及ECDLP的算法的攻击。



参考
https://github.com/Qiskit/textbook/blob/main/notebooks/ch-algorithms/shor.ipynb
https://qluoshu-v17.readthedocs.io/en/latest/ECDLP/F2k_ECDLP/F2k_ECDLP/
RSA
ECC-ElGamal