省选数学专题

难度升序排序（大概吧）。

[AGC016C] +/- Rectangle

签，虽然国集作业。
贪心是显然的，不说了，这里只考虑正数如何填。

如果\(H\times W-\left\lfloor\frac{H}{h}\right\rfloor\times h\times \left\lfloor\frac{W}{w}\right\rfloor\times w\le \left\lfloor\frac{H}{h}\right\rfloor\times \left\lfloor\frac{W}{w}\right\rfloor\)时，此时全填\(1\)肯定不行，那么要填的就是正整数\(k\)，使得\(k\times(H\times W-\left\lfloor\frac{H}{h}\right\rfloor\times h\times \left\lfloor\frac{W}{w}\right\rfloor\times w)< \left\lfloor\frac{H}{h}\right\rfloor\times \left\lfloor\frac{W}{w}\right\rfloor\)。实测\(500\)左右即可。

点此查看代码

#include<bits/stdc++.h>
using namespace std;
#define rep(i,s,t,p) for(int i = s;i <= t;i += p)
#define drep(i,s,t,p) for(int i = s;i >= t;i -= p)
#ifdef LOCALauto I = freopen("in.in","r",stdin),O = freopen("out.out","w",stdout);
#elseauto I = stdin,O = stdout;
#endif
using ll = long long;using ull = unsigned long long;
using db = double;using ldb = long double;
signed main(){cin.tie(nullptr)->sync_with_stdio(false);int H,W,h,w;cin>>H>>W>>h>>w;if(H%h == 0 && W%w == 0) return cout<<"No\n",0;cout<<"Yes\n";rep(i,1,H,1){rep(j,1,W,1)if(i%h == 0 && j%w == 0) cout<<-(h*w-1)*500-1<<' ';else cout<<500<<' ';cout<<'\n';}
}

[JLOI2015] 骗我呢

反射容斥板子，写详细一点当反射容斥学习笔记了。

先考虑反射容斥是什么。

前置知识

在一个二维平面内，只能向右走或向上走，从\((0,0)\)走到\((n,m)\)的方案数是\(\mathrm{C}_{n+m}^n\)的，下文中，若无特殊说明，那么\(P(n,m)\)均表示从\((0,0)\)只能向右走或向上走走到\(n,m\)的方案数，即\(P(n,m)=\mathrm{C}_{n+m}^n\)。

证明

发现每种合法路径必然走了\(n+m\)步，且有\(n\)步向右，\(m\)步向上。所以答案就是从\(n+m\)步中选\(n\)步为向右走的方案数，即\(\mathrm{C}_{n+m}^n\)。

考虑如果有一条直线\(y=x+b\)不可碰撞（\(n+b>m\)）。考虑一个经典trick，就是将所有碰到这条直线的路径，从第一次碰到这条直线处翻折，那么这条路径的终点就是\((m-b,n+b)\)。举个例子（\(y=x+1,n=m=3\)）。

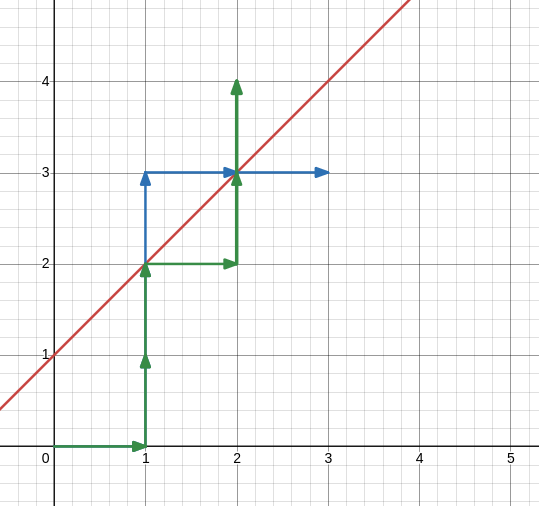
显然答案就是\(P(n,m)-P(m-b,n+b)\)。至于为什么不考虑碰撞两次的，因为每次翻折以后都重合了，没必要考虑。

反射容斥

已经解决了只不允许碰撞一条线的，那么如果存在两条线（\(A:y=x+a,B:y=x+b\;(b<a,n+b<m<n+a)\)）呢？

考虑不合法的方案形如依次经过\(AABBABAB\)，显然重复经过同一条直线没有意义，所以缩成\(ABABAB\)。

显然答案为总方案数\(-A\ldots-B\ldots\)，发现后面的东西是递推的，直接求就行了。

关于本题

由\(x_{i,j}<x_{i,j+1}\)，可知每一行是从左到右单调递增的，由\(0\le x_{i,j}\le m\)可知，每行一定有一个数没有被用上，那么就设\(f_{i,j}\)表示第\(i\)行第\(j\)个数没有填过，考虑转移。由\(x_{i,j}<x_{i-1,j+1}\)可知，\(f_{i,j}=\sum\limits_{k=0}^{j+1}f_{i-1,k}\)，可以手动模拟证明上界为\(j+1\)，显然答案为\(f_{n+1,m}\)，前缀和优化可以做到\(O(nm)\)。

考虑优化这个柿子，会发现\(f_{i,j}=f_{i,j-1}+f_{i-1,j+1}\)，然后将其画到二维平面上，注意这里\(n\)为纵坐标。

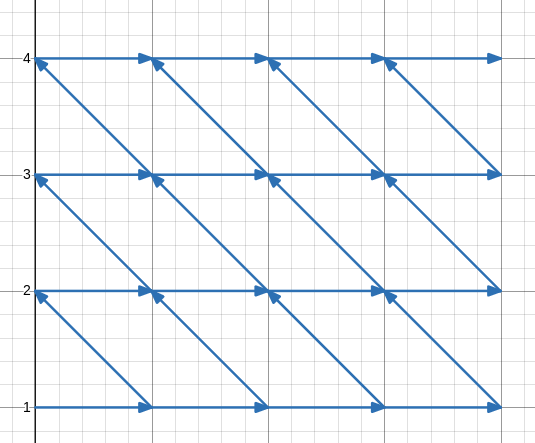
感觉这个不好看，把它拉伸一下。（图是贺的）

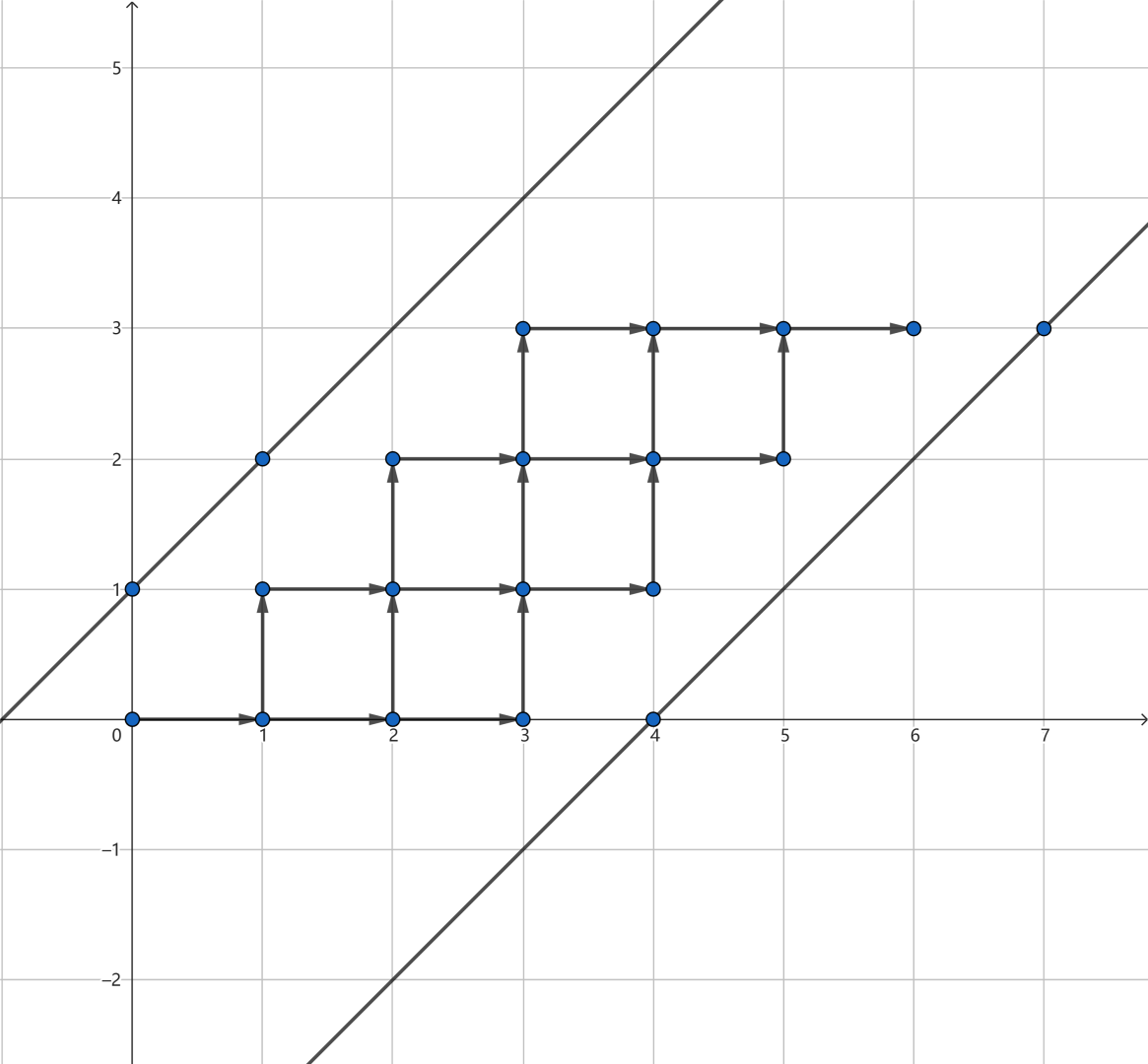
发现就是从\((0,0)\)走到\((n+m+1,n)\)，且不碰\(A:y=x+1,B:y=x-m-2\)的方案数，直接套反射容斥就行了，时间复杂度\(O(n)\)。

点此查看代码

#include<bits/stdc++.h>
using namespace std;
#define rep(i,s,t,p) for(int i = s;i <= t;i += p)
#define drep(i,s,t,p) for(int i = s;i >= t;i -= p)
#ifdef LOCALauto I = freopen("in.in","r",stdin),O = freopen("out.out","w",stdout);
#elseauto I = stdin,O = stdout;
#endif
using ll = long long;using ull = unsigned long long;
using db = double;using ldb = long double;
const int N = 3e6 + 10,MN = 3e6,mod = 1e9 + 7;
int n,m,fac[N],inv[N];
int qpow(int a,int b,int mod){int res = 1;for(;b;b >>= 1,a = 1ll*a*a%mod)if(b & 1) res = 1ll*res*a%mod;return res;
}
int Inv(int a,int mod = mod){return qpow(a,mod-2,mod);}
int C(int n,int m){if(n < 0 || m < 0 || m > n) return 0;return 1ll*fac[n]*inv[m]%mod*inv[n-m]%mod;}
void flip(int &a,int &b,int x){swap(a,b);a -= x;b += x;}
signed main(){cin.tie(nullptr)->sync_with_stdio(false);cin>>n>>m;fac[0] = 1;rep(i,1,MN,1) fac[i] = 1ll*fac[i-1]*i%mod;inv[MN] = Inv(fac[MN]);drep(i,MN-1,0,1) inv[i] = 1ll*inv[i+1]*(i+1)%mod;int ans = C(n*2+m+1,n);int x = n + m + 1,y = n;while(x >= 0 && y >= 0){flip(x,y,1);ans -= C(x+y,x);ans += mod;ans %= mod;flip(x,y,-(m+2));ans += C(x+y,x);ans %= mod;}x = n + m + 1,y = n;while(x >= 0 && y >= 0){flip(x,y,-(m+2));ans -= C(x+y,x);ans += mod;ans %= mod;flip(x,y,1);ans += C(x+y,x);ans %= mod;}cout<<ans<<'\n';
}

[AGC049D] Convex Sequence

模拟赛原，但是当时没改。

考虑将\(2\times a_i\le a_{i-1}+a_{i+1}\)换成\(a_i-a_{i-1}\le a_{i+1}-a_i\)，发现这就是告诉你斜率单调递增。

假设最小值所在位置为\(p\)，那么显然有\(\forall 1\le i<p,a_i<a_{i-1},\forall p< i\le n,a_i<a_{i+1}\)。

假设某一个合法方案的第一个最小值所在位置为\(p\)，那么显然可以通过以下的流程还原这个方案。

1. 将\(a\)中的所有数设为\(C\)，此操作只会再最开始进行一次。
2. 选择一个\(i<p\)，将\(a_i,a_{i-1},\ldots,a_1\)加上\(1,2,3,\ldots\)，此操作可以进行任意次。
3. 选择一个\(i>p\)，将\(a_i,a_{i+1},\ldots,a_n\)加上\(1,2,3,\ldots\)，此操作可以进行任意次。

当固定\(p\)时，那么显然问题转化为：有任意多个\(n,1,3,6,10,\ldots\)，求凑出和为\(m\)的数有多少种方案。

注意\(p\)的定义为第一个最小值所在的位置，所以前面的数至少都加过一次，所以需要凑出的数实际为\(m-p\times (p-1)/2\)。

剩下的，发现就是一个完全背包问题，但是每次重新做的话复杂度是\(O(nm\sqrt{m})\)的。不可接受。发现这个dp是可撤销的，每次统计答案前直接撤销即可，发现每个最多会撤销\(\sqrt m\)个数，每次撤销复杂度是\(O(m)\)的。所以总的时间复杂度就是\(O(m\sqrt m)\)。

点此查看代码

#include<bits/stdc++.h>
using namespace std;
#define rep(i,s,t,p) for(int i = s;i <= t;i += p)
#define drep(i,s,t,p) for(int i = s;i >= t;i -= p)
#ifdef LOCALauto I = freopen("in.in","r",stdin),O = freopen("out.out","w",stdout);
#elseauto I = stdin,O = stdout;
#endif
using ll = long long;using ull = unsigned long long;
using db = long double;using ldb = long double;
const int N = 1e5 + 10,mod = 1e9 + 7;
int n,m,f[N];
signed main(){cin.tie(nullptr)->sync_with_stdio(false);cin>>n>>m;f[0] = 1;auto Add = [&](int x){rep(i,x,m,1) f[i] = (f[i] + f[i-x])%mod;};auto Del = [&](int x){drep(i,m,x,1) f[i] = (f[i] - f[i-x] + mod)%mod;};if(n <= m) Add(n);for(ll i = 1;i < n && i*(i+1)/2 <= m; ++i) Add(i*(i+1)/2);int ans = 0;rep(i,1,n,1){if(1ll*i*(i-1)/2 <= m) ans = (ans + f[m-i*(i-1)/2])%mod;if(1ll*(n-i)*(n-i+1)/2 <= m) Del((n-i)*(n-i+1)/2);if(1ll*i*(i+1)/2 <= m) Add(i*(i+1)/2);}cout<<ans<<'\n';
}

[ABC221H] Count Multiset

套路：多重集合转不下降序列。

先不考虑限制，设\(f_{i,j}\)表示已经填了\(i\)个数，和为\(j\)的方案数。将多重集合转为不下降序列，那么就有两种操作。

1. 将一个\(0\)填入，有\(f_{i,j}=f_{i-1,j}\)。
2. 将全局加一，有\(f_{i,j}=f_{i,j-i}\)

但是有相同的数不能出现超过\(m\)次，那么就是限制连续填入\(0\)的次数为\(m\)，那么第一种操作的贡献为\(\sum\limits_{k=1}^mf_{i-k,j}\)，但由于不知道\(f_{i,j}\)中有多少个\(0\)，考虑再设一个dp数组\(g_{i,j}\)表示当前填了\(i\)个数，总和为\(j\)，且序列中不含\(0\)的方案数，那么有转移方程\(g_{i,j}=f_{i,j-i}\)。

总的转移方程就是

\[f_{i,j}=f_{i,j-i}+\sum_{k=1}^mg_{i-k,j} \]

\[g_{i,j}=f_{i,j-1} \]

前缀和优化可以做到\(O(n^2)\)。

点此查看代码

#include<bits/stdc++.h>
using namespace std;
#define rep(i,s,t,p) for(int i = s;i <= t;i += p)
#define drep(i,s,t,p) for(int i = s;i >= t;i -= p)
#ifdef LOCALauto I = freopen("in.in","r",stdin),O = freopen("out.out","w",stdout);
#elseauto I = stdin,O = stdout;
#endif
using ll = long long;using ull = unsigned long long;
using db = long double;using ldb = long double;
const int N = 5e3 + 10,mod = 998244353;
int n,m,f[N][N],g[N][N],sum[N][N];
signed main(){cin.tie(nullptr)->sync_with_stdio(false);cin>>n>>m;rep(i,1,n,1){if(i <= m) f[i][0] = 1;rep(j,1,n,1){if(j >= i) g[i][j] = f[i][j] = f[i][j-i];sum[i][j] = (sum[i-1][j] + g[i][j])%mod;f[i][j] = (0ll + f[i][j] + sum[i-1][j] - sum[max(0,i-m-1)][j] + mod) % mod;}}rep(i,1,n,1) cout<<g[i][n]<<'\n';
}

\(to\; be\; continued\)