题目链接
很有道理的题。
把划分集合的方案容斥一下,变成染色的方案。
再从边界情况考虑问题。
链
设当前钦定有 \(x\) 种颜色。
从前往后考虑每个点的贡献。
容易发现,它与在它之前的 k-邻域内任意一点颜色不同即可满足条件。
而它之前 k-邻域内的任意两点颜色也是不同的。
所以它对答案的贡献就是 \((x-p)\),其中 \(p\) 是它之前 k-邻域内的点数。
所以容斥后的答案就是关于 \(x\) 的 \(O(n)\) 个一次多项式乘起来。
分治 NTT 和多项式多点求值就可以 \(O(n\log^2 n)\) 解决。
菊花
仿照链的思路,把贡献拆到点上,并找到每个点要和多少个其他点颜色不同。
按照到根的边权从小到大排序,增量地增加点,那么要求它与之前的一个前缀内的点颜色不同,而这个前缀内的点两两也是不同的。
求答案的方法可以仿照链。
一般情况
如果对于一个点 \(u\) 的儿子,依然按照到 \(u\) 的边权排序求贡献,会出现下面的问题:
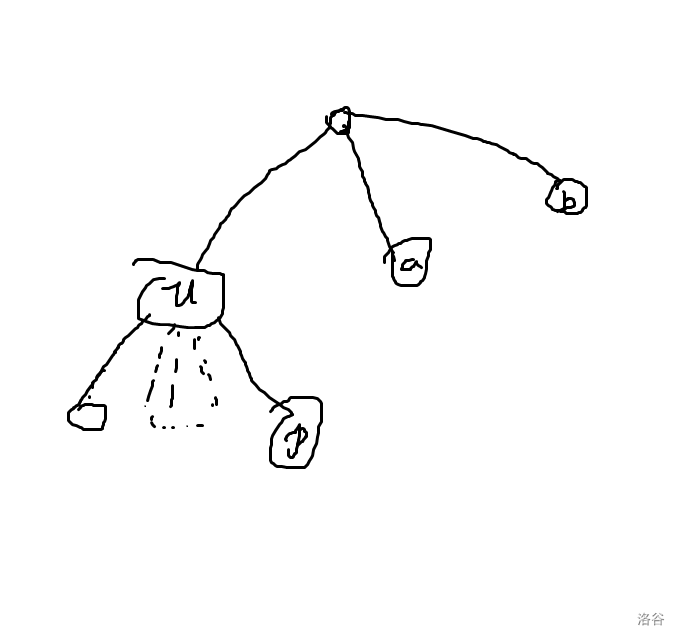
\(dis_{a,p}\leq k\) 且 \(dis_{b,p}\leq k\),但 \(dis_{a,b}>k\)。
此时 \(a,b\) 的颜色可能相同。
所以要找另一种增量顺序规避这种情况。
注意到按照到根节点的距离增量即可。
至此就得到了每个点的贡献 \((x-p)\)。计数的部分依然是仿照链。
而对于每个点求 \(p\),可以点分治,变成二维数点。
总的时间复杂度就是 \(O(n\log^2 n)\) 的。
https://qoj.ac/submission/820388
多点求值似乎有些太困难了。由于只需要求 \(1\) 到 \(n\) 的点值,可以用下降幂多项式。


![[HTML/Web] HTML5之`Video`元素](https://blog-static.cnblogs.com/files/johnnyzen/cnblogs-qq-group-qrcode.gif?t=1679679148)