PERIODNI

news/2024/12/22 20:26:20/文章来源:https://www.cnblogs.com/YzaCsp/p/18622482

思路

哇, 看到这个就直接想到昨天学的经典应用 : 最大子矩形

好吧还是认真推一下

完蛋了是计数, 我们没救了

首先按照高度为优先级, 位置为键值建一颗小根笛卡尔树, 我们玩下样例找下性质

例如题目中给出的图片, 我们建成笛卡尔树就长这样

pAOLNpq.md.png

其中每个点由 \(\{键值, 优先级\}\) 组成

观察这颗笛卡尔树, 我们看看有什么性质

容易发现每个点如果要放上数字, 那么一定只能放一个, 因为题目中明确说明 "不得有任意两个数在同一行或者同一列"

好吧不太会做, 我们去看下 \(\rm{TJ}\)

\(\rm{Part \ 1}\) : 笛卡尔树分割多边形

这里有一个前置知识, 也就是在规范的四边形中, 这个问题应当如何求解

pAOLD74.md.png

那么我们想办法把这些多边形拆开方便计算, \(\rm{belike}\) :

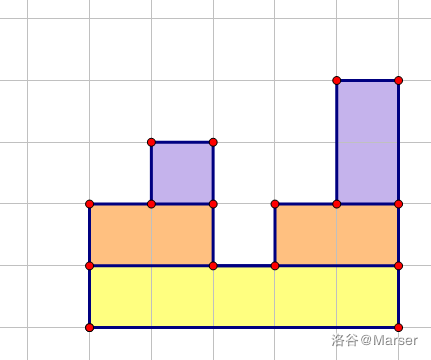
这样构成的若干个矩形正好满足笛卡尔树的性质:

pAOL0nU.md.png

你发现我们之前对 \(\{h_i\}\) 建树, 不刚好就长这样吗
具体的, 一定是 \(h_i\) 小的点更早被分割, 善哉, 完美符合要求
一个小问题是有可能有些情况会出现不能恰好分成二叉的情况, 但是你发现这种情况下可以将其二度化照样处理, \(\rm{belike}\) :
pAOvcVO.md.png

\[\Downarrow \]

pAOv2Ie.md.png

在实现上, 你只需要把每次分割不全的部分合到一起丢下去下次在分开即可, 当然如果用笛卡尔树建那就不用管

注意对于笛卡尔树上的点, 我们都需要记录其长以及宽, 以下设为 \(L_i, H_i\)

时间复杂度 : \(\mathcal{O} (n)\)

\(\rm{Part \ 2}\) : 树上背包

有了以上的知识, 我们就可以把这个题转化成一个在树上做背包的计数类问题

具体怎么做? ~~先学一下树上背包~~

把 \(u\) 子树上的点看做一个组, 把 \(u\) 子树中所有点的最大取点和看做容量, 每个点看做物品, 体积为 \(1\) \(\cdots\)

其实个人认为不需要这么复杂, 树上依赖的背包问题, 仅仅只是把状态的一维定义成了当前的 "容量" , 也不用去刻意的套

令 \(f_{i, j}\) 表示 \(i\) 及 \(i\) 的子树中, 取了 \(j\) 个互不冲突的点的可能性, 记 \(i\) 的左儿子为 \(l\) , 右儿子为 \(r\)

显然的, 这相当于在笛卡尔树上进行树形 \(\rm{dp}\) , 由于其良好的二叉树性质, 还是很好处理的

找一个朴素的转移, 不难写出 (需要注意的是每个点互不相同, 题目没有明确表述)

\[f_{i, j} = \sum_{k = 0}^{j} \sum_{h = 0}^{j - h} f_{l, k} \cdot f_{r, h} \cdot {L_i \choose j - k - h} \cdot {H_i \choose j - k - h} \cdot {(j - k - h)}! \]

初始化每个叶子结点 \(i\) : \(f_{i, j} = {L_i \choose j} \cdot {H_i \choose j } \cdot j!\)

答案即为 \(f_{root, k}\)