MADDPG算法

news/2024/12/23 0:28:30/文章来源:https://www.cnblogs.com/usersname/p/18622832

MADDPG算法

论文名称：《Multi-Agent Actor-Critic for Mixed Cooperative-Competitive Environments》

一、基本问题

MADDPG是一篇经典的多智能体强化学习算法。在MADDPG以前，多智能体强化学习算法主要为独立学习技术。

独立学习技术

独立学习技术就是在环境中对于每一个智能体单独的使用单智能体强化学习的算法。比如独立学习的典型算法IQL算法（Independent Q Learning）就是在多智能体环境下单独的使用Q Learning算法。
独立学习技术的优缺点

使用独立学习技术，可以有效解决环境复杂的问题。在多智能体强化学习中，智能体的动作空间一般是所有智能体动作的联合空间。如果智能体的数量巨大，这个联合空间也是十分巨大的。这对于模型来说是一个巨大的负担。如果使用独立学习技术，就不存在这个负担，因为独立学习直接假设其他智能体也是环境的一部分。

所以独立学习也有非常明显的缺点，就是直接假设其他智能体也是环境的一部分。在多智能体环境下，特别是需要智能体之间进行合作或者博弈等场景下，智能体之间往往需要有一定的交流，面对这样的场景，独立学习需要针对场景做出特殊的优化。并且智能体的动作可能会导致环境的不稳定，最终导致整个模型无法收敛。所以独立学习技术局限性较大。

MADDPG算法就是为了克服独立学习的以上缺点而提出一种通用性强的算法。

二、基础知识

2.1 DDPG算法

DDPG算法，以AC框架为基础，借鉴DQN算法的思想，主要是为了解决高维连续动作空间的问题而提出。相较与传统的AC框架使用策略梯度更新Actor网络。即：

\[J(\theta) = -log(\pi(a_t,s_t)) Advantage \space Function \tag{1} \]

式（1）中，Advantage Function 表示优势函数。在传统AC中，Advantage Function 直接取 \(Q(s_t,a_t)\)。在A2C算法中发现在Advantage Function 中加入Baseline可以提高模型效果。并且通常情况下我们取 Baseline 为 \(V(s_{t+1}) = \mathbb{E}_{a\sim \pi}[R_{t+1} + \gamma Q(s_{t+1},a_{t+1})]\)。也就是公式（1）的最终形式：

\[J(\theta) = -log(\pi(s_t|a_t))[Q(s_t,a_t) - (R_{t+1} + \gamma Q(s_{t+1},a_{t+1}))] \tag{2} \]

而在DDPG算法中，使用了确定性策略梯度。确定性策略梯度的目标是最大化动作对应Q值。也就是：

\[\begin{equation} \begin{aligned} J(\theta) &= -Q(s_t, \mu_{\theta}(s_t)) \\ \\ \nabla J(\theta) &= - \nabla Q(s_t,\mu(s_t))\nabla\mu_{\theta}(s_t) \end{aligned} \end{equation} \tag{3} \]

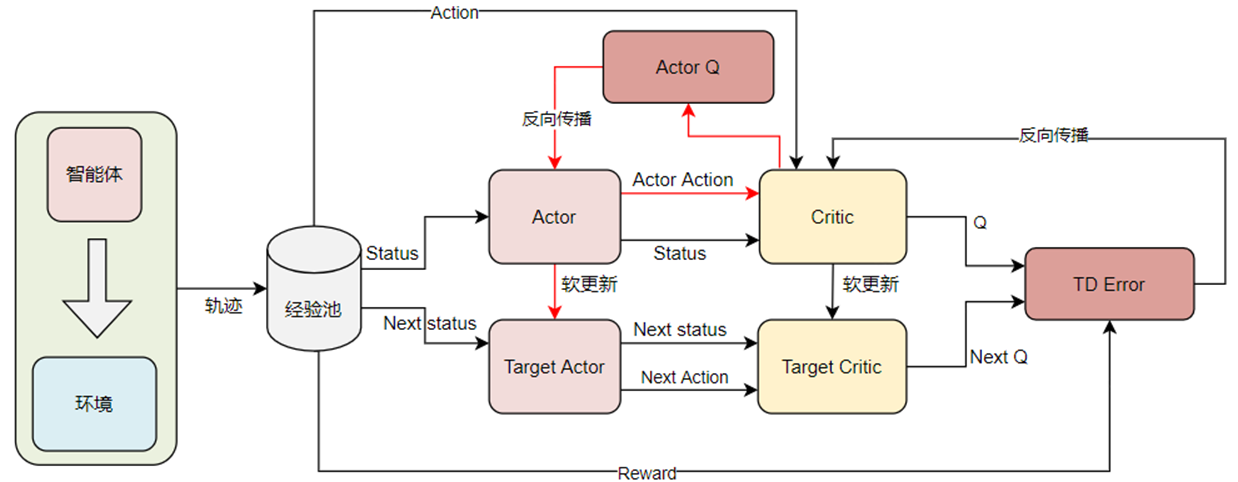
公式(3)中 \(\mu\) 表示策略网络。总体来说DDPG算法可以使用下面的流程图来表示：

2.2 多智能体训练范式

2.2.1 CTDE 范式

CTDE（centralized training and decentralized execution）中文名叫做集中式训练，分布式执行。该方式，通过一个全局的Critic网络评估每一个智能体动作或者状态的价值。CTDE范式的示意图如下：

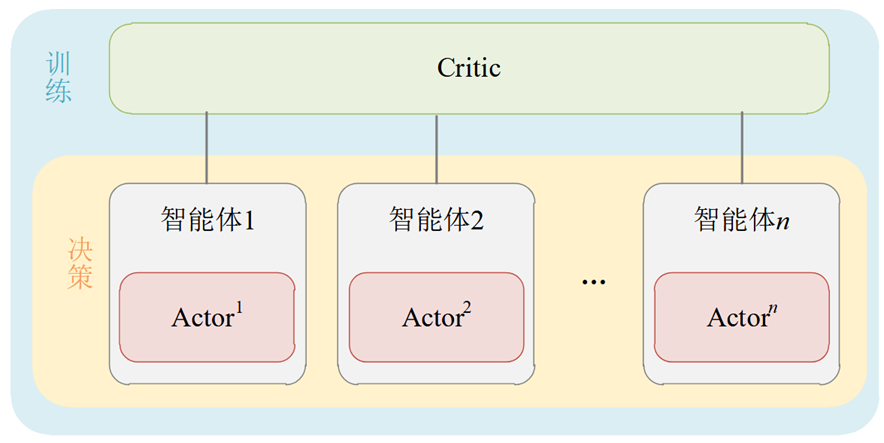
使用CTDE范式的典型代表有VDN算法、QMIX算法。总体来说，CTDE范式可以有效的解决智能体懒惰的问题（在其他智能体动作较好的时候，如果有一个智能体动作较差，环境整体的奖励还是较大，久而久之，智能体就会开始摸鱼）。但是CTDE范式的智能体观察依旧是局部的，智能体不能有效利用其他智能体的信息进行决策。

2.2.2 DTDE 范式

DTDE（decentralized training and centralized execution）中文名叫分散式训练，集中式执行。该范式在所有智能体动作之后，将全局的信息送往每一个Critic网络。DTDE范式的示意图如下：

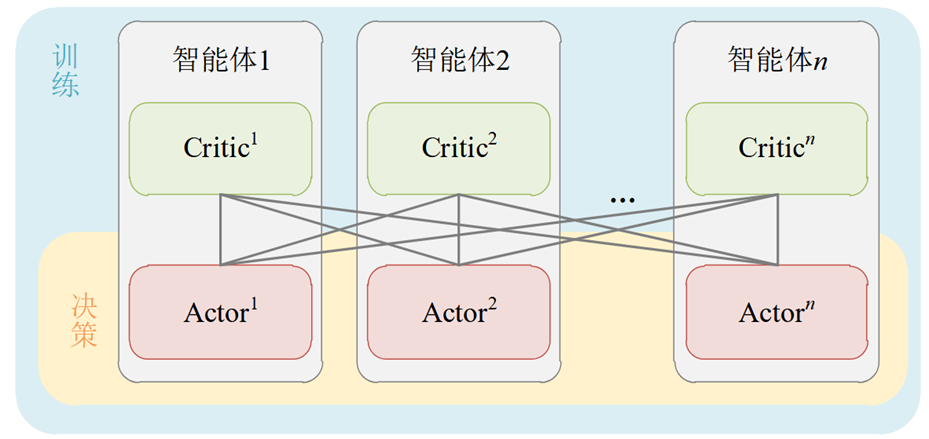
使用DTDE范式的典型代表就是MADDPG算法。总体来说，DTDE相对于CTDE不需要维护中心化的Critic，更加简单方便，但是相对来说智能体的观察也更加局部，容易陷入局部最优，并且依旧存在维度爆炸的问题。

三、MADDPG算法

MADDPG算法使用的DTDE范式。在每一个智能体上运行DDPG算法。但是相较于传统的DDPG算法，MADDPG算法做出了一定的修改。

由于使用了DTDE范式，所以对于每一个Criric都需要输入其他Actor的动作。但是实际上，在多智能体环境下，我们不能假设我们知道其他智能体的动作。所以对于每一个Agent，都需要对其他智能体维护一个Target Policy，来预测其他智能体的在当前状态下的动作，注意这里Target Policy的输入是其他智能体的在该智能体状态下的观察值。该策略使用在线的方式更新，更新的损失函数为：

\[J(\phi_i^j) = -\mathbb{E}_{o_j,a_j}\left[\log \hat{\mu}_i^j(a_j|o_j) + \alpha H(\hat{\mu}_i^j)\right] \tag{4} \]
在公式(4)中， \(\hat{\mu}_i^j\) 表示第 \(i\) 个智能体对 \(j\) 个智能体维护的目标策略网络。 \(o_j\) 表示该网络的观察值， \(a_j\) 表示第 \(j\) 个智能体的实际动作。 \(H(\hat{\mu}_i^j)\) 表示熵，目的是防止网络过拟合，超参数 \(\alpha\) 用来控制熵的大小。总的来说，公式(4)的目标是使得目标网络输出的动作概率分布尽可能的逼近真实的动作。
接1，虽然公式(4)中加入了熵在一定程度上防止目标策略网络过拟合。但是这种方式也不总是非常有效。特别是在博弈环境中，目标策略网络特别容易拟合对手的策略。论文中认为，这种拟合是脆弱的，因为一旦对手修改了策略，那么目标策略网络将完全失效。为了应对这种情况，作者提出每一个智能体维护一个目标策略网络的集合。该集合中有 \(k\) 组策略网络。每次训练随机选取一组进行梯度下降。在论文的实验中表明，使用这种方式训练的智能体具有更加强大的泛化性。
DDPG算法的提出是为了解决高维连续动作空间的问题。但是MADDPG的实验部分却将DDPG算法应用在离散动作空间下。但是如果直接使用Soft Max函数输出每一个动作的概率，就需要进行采样才能确定动作，进一步传递给 \(Q\)网络计算 \(Q\)值。但是采样操作是不可导的，也就是我们无法计算公式(3)。所以在论文中，作者提到使用 gumbel-softmax可以解决这个问题。
- gumbel-softmax
  
  gumbel-softmax 的核心是重参数技巧。简单来说，gumbel-softmax的原理可以概括为，在某个分布中不断选择概率最大的值的概率也对应着一个分布，这个分布就是gumbel分布。gumbel-softmax就通过gumbel分布将 Actor输出的概率分布采样动作(选取概率最大的动作)转化为了gumbel 分布，而gumbel分布是连续可导的。而gumbel分布的计算利用了重参数技巧。