普通莫队
详介(P2709 小B的询问)
普通莫队处理问题的前提是问题可以离线,多次区间查询,\(O(n\sqrt m)\) 能过。
我们以 P2709 小B的询问 为例,假设当前区间为 \([l,r]\),答案为 \(ans\),那么 \(r\) 右移一位时,新加入一个数 \(x\),我们只要把 \(ans\) 加上 \(x\) 的贡献即可。贡献只需要维护一下当前区间内 \(x\) 的出现次数 \(cnt[x]\) 即可。
所以我们可以初始 \(l = 1, r = 0\),每次向一个询问的区间移动 \(l\) 和 \(r\),然后维护当前区间的答案。
我们发现,如果两个查询区间的差距很大,我们每次就要跑很远才能到答案,所以我们要将所有的询问离线下来,进行分块和排序。
具体地,我们将所有的询问进行分块,将所有的询问按照左端点所在块为第一关键字,右端点升序进行排序,这样排完序后我们发现在一个块中 \(r\) 的移动为 \(O(n)\),设当前块长为 \(B\),那么总共就是 \(O(\frac{n^2}{B})\),而左端点在每两个询问之间移动次数不超过 \(O(B)\),所以总共为\(O(mB)\),两者相加就是 \(O(mB + \frac{n^2}{B})\)。发现取 \(B\) 为 \(\frac{n}{\sqrt m}\) 时复杂度最优为 \(O(n\sqrt m)\)。
这是 \(P2709\) 的代码。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 50010;
int n, m, k, w[N], B, cnt[N], ans[N];
LL res;struct node {int l, r, id;bool operator < (const node &t) const {if (l / B == t.l / B) return r < t.r;else return l / B < t.l / B;}
} q[N];void add(int x) {res -= cnt[x] * cnt[x];cnt[x] ++;res += cnt[x] * cnt[x];
}void del(int x) {res -= cnt[x] * cnt[x];cnt[x] --;res += cnt[x] * cnt[x];
}int main() {scanf("%d%d%d", &n, &m, &k); B = sqrt(n);for (int i = 1; i <= n; i ++) scanf("%d", &w[i]);for (int i = 1; i <= m; i ++) { scanf("%d%d", &q[i].l, &q[i].r); q[i].id = i; }sort(q + 1, q + 1 + m);int l = 1, r = 0;for (int i = 1; i <= m; i ++) {while (l > q[i].l) add(w[-- l]);while (r < q[i].r) add(w[++ r]);while (l < q[i].l) del(w[l ++]);while (r > q[i].r) del(w[r --]);ans[q[i].id] = res;}for (int i = 1; i <= m; i ++) printf("%d\n", ans[i]);return 0;
}
P1494 小 Z 的袜子
这同样是一道莫队题,我们发现答案应该是:
其中 \(col\) 是 \([L,R]\) 中出现的所有颜色,\(cnt_{col}\) 是该颜色出现的次数,我们修改一下莫队的 \(add\) 和 \(del\),维护分子即可。
记得约分和特判。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 50010;
int n, m, k, w[N], B, cnt[N], ans[N], ans2[N];
LL res;struct node {int l, r, id;bool operator < (const node &t) const {if (l / B == t.l / B) return r < t.r;else return l / B < t.l / B;}
} q[N];void add(int x) {res -= cnt[x] * (cnt[x] - 1) / 2;cnt[x] ++;res += cnt[x] * (cnt[x] - 1) / 2;
}void del(int x) {res -= cnt[x] * (cnt[x] - 1) / 2;cnt[x] --;res += cnt[x] * (cnt[x] - 1) / 2;
}LL gcd(LL a, LL b) {return b ? gcd(b, a % b) : a;
}int main() {scanf("%d%d", &n, &m); B = sqrt(n);for (int i = 1; i <= n; i ++) scanf("%d", &w[i]);for (int i = 1; i <= m; i ++) { scanf("%d%d", &q[i].l, &q[i].r); q[i].id = i; }sort(q + 1, q + 1 + m);int l = 1, r = 0;for (int i = 1; i <= m; i ++) {while (l > q[i].l) add(w[-- l]);while (r < q[i].r) add(w[++ r]);while (l < q[i].l) del(w[l ++]);while (r > q[i].r) del(w[r --]);ans[q[i].id] = res; ans2[q[i].id] = (LL)(r - l + 1) * (r - l) / 2;}for (int i = 1; i <= m; i ++) {if (ans[i] == 0) ans2[i] = 1;LL g = gcd(ans[i], ans2[i]);printf("%lld/%lld\n", ans[i] / g, ans2[i] / g);}return 0;
}
可能还有例题,后面再做。
带修莫队
详介
带修莫队可以理解为一种广义高维莫队,顾名思义,可以支持修改。做法也十分简单,我们只需要给莫队增加一维时间即可。时间指的是在这个查询操作前一共有多少个修改操作。由于加了一维时间,所以我们可以按照第一维左端点所在块,第二维右端点所在块,第三维时间,分别从小到大排序。
struct query {int l, r, id, t;bool operator < (const query &T) const {if (l / B != T.l / B) return l / B < T.l / B;else if (r / B != T.r / B) return r / B < T.r / B;else return t < T.t;}
} q[N];
同时我们还需要存一下所有的修改操作。
struct operation {int p, x;
} op[N];
莫队如何维护时间维呢?我们发现如果当前的修改的 \(p\) 属于当前莫队区间 \([l,r]\),那么就对第 \(p\) 个位置原本的数 \(y\) 做 \(del(y)\),然后再对于修改的 \(x\) 做 \(add(x)\),最后由于每一个修改操作的使用和清除一定是成对出现的,所以我们直接将 \(x\) 和 \(y\) 进行交换即可。
void upd(int last, int l, int r) { // last 是当前操作编号if (op[last].p >= l && op[last].p <= r) {add(op[last].x);del(a[op[last].p]);}swap(op[last].x, a[op[last].p]);
}
我们再考虑块长应该取多少,我们直接考虑 \(k\) 维莫队,其中前 \(k - 1\) 维按所在块升序,第 \(k\) 维升序,那么一共会出现 \((\frac{n}{B})^{k-1}\) 种块的情况,每种情况下右端点最多移动 \(O(n)\),每切换一次询问左端点最多移动 \(O((k-1)B)\),所以总的时间复杂度就应该是 \(O((\frac{n}{B})^{k-1} \times n + (k-1)Bm)\),根据基本不等式当 \(B = \sqrt[k]{\frac{n^k}{(k-1)m}}\) 时取到最优,如果将 \((k-1)\) 视为常数,并且 \(n、m\) 同阶,那么 \(B\) 就可以取到 \(n^{\frac{k-1}{k}}\)。
回到带修莫队,就相当于一个三维的莫队,那么 \(B\) 就取 \(n^{\frac{2}{3}}\),带回计算可得到时间就是 \(O(n^{\frac{5}{3}} + 2 \times n^{\frac{1}{3}}m)\),可以看做 \(O(n^{\frac{5}{3}})\)。
例题 P1903 数颜色
贴一份带修莫队的代码。
#include <bits/stdc++.h>
using namespace std;
const int N = 150010, M = 1000010;
int n, m, a[N], B;
int cnt[M], res, qcnt, opcnt;
int ans[N];struct query {int l, r, id, t;bool operator < (const query &T) const {if (l / B != T.l / B) return l / B < T.l / B;else if (r / B != T.r / B) return r / B < T.r / B;else return t < T.t;}
} q[N];struct operation {int p, x;
} op[N];void add(int x) {if (!cnt[x]) res ++;cnt[x] ++;
}void del(int x) {cnt[x] --;if (!cnt[x]) res --;
}void upd(int last, int l, int r) {if (op[last].p >= l && op[last].p <= r) {add(op[last].x);del(a[op[last].p]);}swap(op[last].x, a[op[last].p]);
}int main() {scanf("%d%d", &n, &m);for (int i = 1; i <= n; i ++) scanf("%d", &a[i]);B = pow(n, 2.0 / 3.0);for (int i = 1; i <= m; i ++) {char t[2]; int l, r;scanf("%s%d%d", t, &l, &r);if (*t == 'Q') q[++ qcnt] = {l, r, qcnt, opcnt};else op[++ opcnt] = {l, r};}sort(q + 1, q + 1 + qcnt);int l = 1, r = 0, last = 0;for (int i = 1; i <= qcnt; i ++) {while (l > q[i].l) add(a[-- l]);while (r < q[i].r) add(a[++ r]);while (l < q[i].l) del(a[l ++]);while (r > q[i].r) del(a[r --]);while (last < q[i].t) upd(++ last, l, r);while (last > q[i].t) upd(last --, l, r);ans[q[i].id] = res;}for (int i = 1; i <= qcnt; i ++) printf("%d\n", ans[i]);return 0;
}
树上莫队
详介 (SP10707 COT2 - Count on a tree II)
顾名思义,是在“树上”的莫队。我们来看一个例子(就是本段标题的题目),要求树上路径上的不同颜色数。
我们发现在树上进行莫队十分的不方便,我们考虑将其转化成一维的序列。我们可以使用欧拉序。
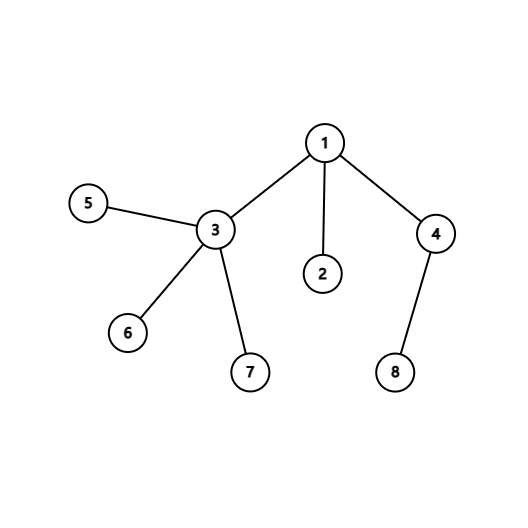
对于这幅图,它的欧拉序(以 \(1\) 为更)便是 \([1,3,5,5,6,6,7,7,3,2,2,4,8,8,4,1]\)。我们考虑一个点 \(u\) 到 \(v\) 的路径在欧拉序中的表示,我们记 \(st[x]\) 和 \(ed[x]\) 分别表示一个点的第一次和最后一次出现的位置,那么我们可以分类讨论(假定 \(st[u] < st[v]\)):
- \(u\) 是 \(v\) 的祖宗,如 \(1 -> 6\),我们可以截取欧拉序中的 \([1,3,5,5,6]\),即 \(st[1] \sim st[6]\) 之间的所有。我们发现 \(5\) 出现了两次,相当于进去了有出来,可以删掉,剩下的 \([1,3,6]\) 便是我们的路径。
- \(u\) 不是 \(v\) 的祖宗,如 \(3 -> 8\),那么我们截取 \(ed[3] \sim st[8]\) 之间的所有,再删去出现两次的 \(2\),剩下 \([3,4,8]\) 我们发现路径中还少了 \(3\) 和 \(8\) 的 \(lca\),加上即可。
综上,我们可以将 \(u -> v\) 的路径用欧拉序巧妙的表示。这样子树上的询问就变成区间,可以使用莫队。由于我们使用的是普通莫队,所以块长为 \(\frac{n}{\sqrt m}\)。同时,为了维护一个点的出现次数,我们可以使用异或,\(0\) 表示该点第一次出现,可加入,\(1\) 表示第二次,要删除。
注意到颜色 \(\leq 2e9\),需要离散化。
#include <bits/stdc++.h>
using namespace std;
const int N = 200010, M = 100010;
int n, m, w[N];
int h[N], e[N], ne[N], idx;
int fa[N][20], depth[N], in[N];
int st[N], ed[N], q[N], len;
int vis[N], cnt[N], res, ans[M];
int c[N];
vector<int> v;int find(int x) {return lower_bound(v.begin(), v.end(), x) - v.begin();
}void add_edge(int a, int b) {e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}// lca 的预处理
void bfs(int root) {queue<int> q; q.push(root);memset(depth, 0x3f, sizeof depth);depth[0] = 0, depth[root] = 1;while (q.size()) {int t = q.front(); q.pop();for (int i = h[t]; ~i; i = ne[i]) {int j = e[i];if (depth[j] > depth[t] + 1) {depth[j] = depth[t] + 1;fa[j][0] = t;q.push(j);for (int k = 1; k < 20; k ++) fa[j][k] = fa[fa[j][k - 1]][k - 1];}}}
}// 预处理欧拉序
void dfs(int u, int fa) {q[++ len] = u, st[u] = len;for (int i = h[u]; ~i; i = ne[i]) {int j = e[i];if (j == fa) continue;dfs(j, u);}q[++ len] = u, ed[u] = len;
}// 倍增求 lca
int lca(int a, int b) {if (depth[a] < depth[b]) swap(a, b);for (int k = 19; k >= 0; k --)if (depth[fa[a][k]] >= depth[b])a = fa[a][k];if (a == b) return a;for (int k = 19; k >= 0; k --)if (fa[a][k] != fa[b][k]) {a = fa[a][k];b = fa[b][k];} return fa[a][0];
}int B;
struct query {int l, r, id, lca;bool operator < (const query &t) const {return l / B < t.l / B || l / B == t.l / B && r > t.r;}
} que[N];void add(int x) {if (!cnt[x]) res ++;cnt[x] ++;
}void del(int x) {cnt[x] --;if (!cnt[x]) res --;
}void upd(int x) {if (!vis[x]) add(c[x]);else del(c[x]);vis[x] ^= 1;
}int main() {scanf("%d%d", &n, &m);memset(h, -1, sizeof h);B = n / sqrt(m);for (int i = 1; i <= n; i ++) {scanf("%d", &w[i]);v.push_back(w[i]);}for (int i = 1; i < n; i ++) {int a, b; scanf("%d%d", &a, &b);add_edge(a, b); add_edge(b, a);}sort(v.begin(), v.end());v.erase(unique(v.begin(), v.end()), v.end());for (int i = 1; i <= n; i ++) c[i] = find(w[i]);bfs(1); dfs(1, -1);for (int i = 1; i <= m; i ++) {int u, v; scanf("%d%d", &u, &v);int s = lca(u, v);if (s == u || s == v) {if (st[v] < st[u]) swap(u, v);que[i] = {st[u], st[v], i};} else {if (ed[v] < st[u]) swap(u, v);que[i] = {ed[u], st[v], i, s};}}sort(que + 1, que + 1 + m);int l = 1, r = 0;for (int i = 1; i <= m; i ++) {while (l > que[i].l) upd(q[-- l]);while (r < que[i].r) upd(q[++ r]);while (l < que[i].l) upd(q[l ++]);while (r > que[i].r) upd(q[r --]);if (que[i].lca) upd(que[i].lca);ans[que[i].id] = res;if (que[i].lca) upd(que[i].lca);}for (int i = 1; i <= m; i ++) printf("%d\n", ans[i]);return 0;
}
P4074 糖果公园
注意到题目求的其实就是 \(u->v\) 路径上的 \(\sum_{col\in c_{u->v}}\ v_{col}\times \sum{w_{col}}\),并且需要支持修改,我们使用树上莫队和带修莫队的融合版即可。
代码有点复杂。注意 \(modify\) 中的 \(x\) 是 \(p\) 位置在进行本次修改前应该是什么值,而 \(t\) 存的是本次修改后的值。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 200010;
int n, m, Q;
int v[N], w[N], c[N], last[N];
int h[N], e[N], ne[N], idx;
int fa[N][22], depth[N];
int q[N], st[N], ed[N], len;
LL cnt[N], dis[N], ans[N], cntw[N];
LL res;void add(int a, int b) {e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
} void bfs(int root) {queue<int> q; q.push(root);memset(depth, 0x3f, sizeof depth);depth[0] = 0, depth[root] = 1;while (q.size()) {int t = q.front(); q.pop();for (int i = h[t]; ~i; i = ne[i]) {int j = e[i];if (depth[j] > depth[t] + 1) {depth[j] = depth[t] + 1;fa[j][0] = t;q.push(j);for (int k = 1; k <= 20; k ++) fa[j][k] = fa[fa[j][k - 1]][k - 1];}}}
}void dfs(int u, int fa) {q[++ len] = u, st[u] = len;for (int i = h[u]; ~i; i = ne[i]) {int j = e[i];if (j == fa) continue;dfs(j, u);}q[++ len] = u, ed[u] = len;
}int lca(int a, int b) {if (depth[a] < depth[b]) swap(a, b);for (int k = 20; k >= 0; k --)if (depth[fa[a][k]] >= depth[b])a = fa[a][k];if (a == b) return a;for (int k = 20; k >= 0; k --)if (fa[a][k] != fa[b][k]) {a = fa[a][k];b = fa[b][k];} return fa[a][0];
}int B, qcnt, rcnt;
struct Query {int l, r, id, t, lca;bool operator < (const Query &T) const {if (l / B != T.l / B) return l / B > T.l / B;else if (r / B != T.r / B) return r / B > T.r / B;else return t > T.t;}
} query[N];struct Modify {int p, x, t;
} modify[N];// 写法和上一题不一样,感觉 OIWiki 上的更简洁一点
void add(int x) {if (dis[x]) res -= (LL)v[c[x]] * w[cnt[c[x]]--];else res += (LL)v[c[x]] * w[++ cnt[c[x]]];dis[x] ^= 1;
}void upd(int p, int x) {if (dis[p]) {add(p); c[p] = x; add(p);} else c[p] = x;
} int main() {scanf("%d%d%d", &n, &m, &Q);memset(h, -1, sizeof h);for (int i = 1; i <= m; i ++) scanf("%d", &v[i]);for (int i = 1; i <= n; i ++) scanf("%d", &w[i]);for (int i = 1; i < n; i ++) {int a, b; scanf("%d%d", &a, &b);add(a, b); add(b, a);}for (int i = 1; i <= n; i ++) { scanf("%d", &c[i]); last[i] = c[i]; }bfs(1); dfs(1, -1);B = pow(len, 2.0 / 3.0);while (Q --) {int op, x, y; scanf("%d%d%d", &op, &x, &y);if (op == 0) {// last[x] 表示位置 x 修改前的值modify[++ rcnt] = {x, last[x]};last[x] = modify[rcnt].t = y;} else {int s = lca(x, y);if (s == x || s == y) {if (st[y] < st[x]) swap(x, y);query[++ qcnt] = {st[x], st[y], qcnt, rcnt, 0};} else {if (st[y] < st[x]) swap(x, y);query[++ qcnt] = {ed[x], st[y], qcnt, rcnt, s};}}}sort(query + 1, query + 1 + qcnt);int l = 1, r = 0, last = 0;for (int i = 1; i <= qcnt; i ++) {while (l > query[i].l) add(q[-- l]); while (r < query[i].r) add(q[++ r]);while (l < query[i].l) add(q[l ++]);while (r > query[i].r) add(q[r --]); // 这里注意,拓展时用的是修改后的值,恢复时用的是修改前的值while (last < query[i].t) last ++, upd(modify[last].p, modify[last].t);while (last > query[i].t) upd(modify[last].p, modify[last].x), last --; if (query[i].lca) add(query[i].lca);ans[query[i].id] = res;if (query[i].lca) add(query[i].lca);}for (int i = 1; i <= qcnt; i ++) printf("%lld\n", ans[i]);return 0;
}
回滚莫队
在写