本文记述了用 Matplotlib 在线性坐标系中绘制三角函数图象的例子。
代码主体内容如下:
...def main():fig, axs = plt.subplots(1, 3, figsize=(14,4.5)) #1axs[0] = configure_axes(axs[0], 'Trigonometric Function\t\t\t' + r'$sine$', 2*np.pi, 1, np.pi, np.pi/2, 1, 1/2) #2x = np.linspace(-2*np.pi, 2*np.pi, 300)y = 1/2 * np.sin(2*x + np.pi/3) #3axs[0].plot(x, y, color='b')axs[0].text(3.5, 0.5, r'$y = \frac{1}{2}sin(2x + \frac{π}{3})$', color='b', horizontalalignment='left', verticalalignment='bottom')y = np.sin(x) #4axs[0].plot(x, y, color='k', linestyle=':')axs[0].text(4, -1, r'$y = sin(x)$', color='k', horizontalalignment='left', verticalalignment='top')#5axs[1] = configure_axes(axs[1], '\t\t\t\t\t\t\t' + r'$cosine$', 4*np.pi, 2, np.pi, np.pi/2, 2, 1) #2x = np.linspace(-4*np.pi, 4*np.pi, 300)y = 2 * np.cos(1/2*x - np.pi*2/3) #3axs[1].plot(x, y, color='r')...axs[2] = configure_axes(axs[2], '\t\t\t\t\t\t\t' + r'$tangent$', 3*np.pi, 5, np.pi, np.pi/2, 5, 2.5) #2x1 = np.linspace(-35/12*np.pi, -13/12*np.pi, 100)y1 = np.tan(x1*1/2) #3x2 = np.linspace(-11/12*np.pi, 11/12*np.pi, 100)y2 = np.tan(x2*1/2)x3 = np.linspace( 13/12*np.pi, 35/12*np.pi, 100)y3 = np.tan(x3*1/2)axs[2].plot(x1, y1, x2, y2, x3, y3, color='y')...fig.tight_layout() #6...def configure_axes(ax, title, xlimit, ylimit, xmajorunit = 2*np.pi, xminorunit = np.pi, ymajorunit = 1, yminorunit = 1/2):...if __name__ == '__main__': main()...
在绘图前,准备一个能放下 1x3 个图象的特定大小的区域(#1)。分别配置三个坐标系(#2),其中内容请参考在线性坐标系中绘制一次函数图象。分别用蓝色、红色和黄色实线绘制正弦函数 y = 1/2 * sin(2 * x + π / 3)、余弦函数 y = 2 * cos(1/2 * x - π * 2/3) 、正切函数 y = tan(1/2 * x) 的图象(#3)以及用黑色点线绘制标准正弦、余弦、正切函数图像(#4),并附上数学表达式说明(#5)。最后调整绘图区域大小以填充整个图象区域(#6)。
图象显示如下:
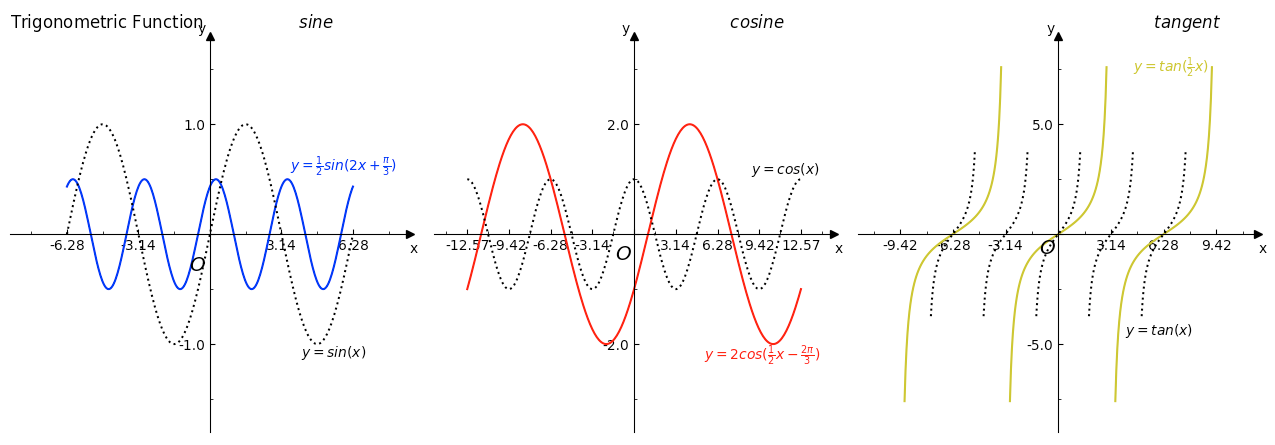
此代码可在 Matplotlib 3.3.4,Python 3.6.8 环境中运行。完整的代码请参考 [gitee] cnblogs/18630399 。
更多例子请参考 函数图象、数据可视化 和 Matplotlib Gallery。