CF2043C Sums on Segments

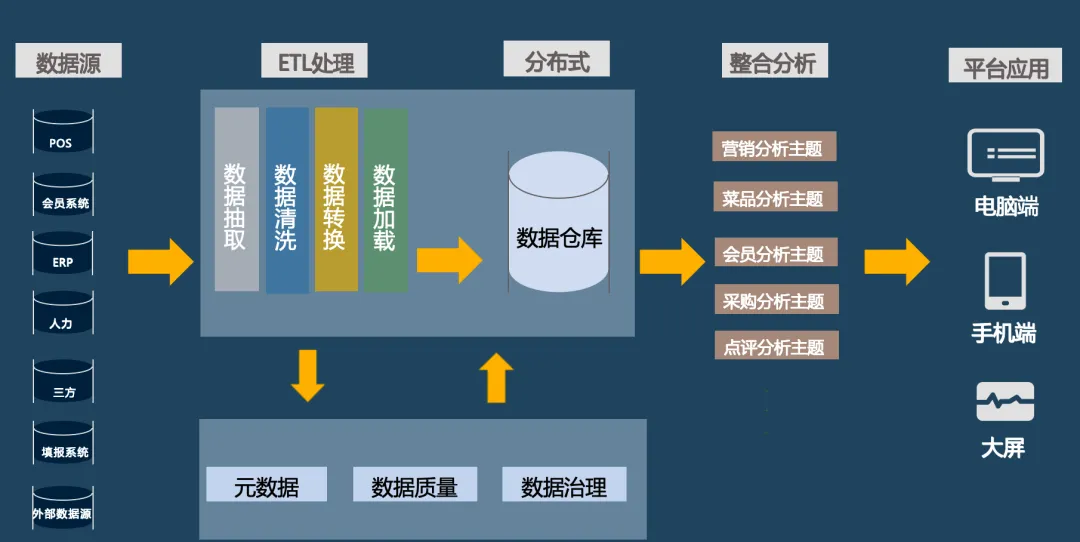
题意概要

一个数组，最多有一个数的绝对值不是 \(1\)，求出所有可以得到的区间和。

思路

这里提供一个 数据结构优化查询前缀和最值 的做法。

最多有一个数的绝对值不是 \(1\)，那我们可以先忽略掉这个数（记该数下标为 \(x\)）。
剩下的数要么是 \(1\)，要么是 \(-1\)，所以我们扩展一个区间的时候，区间和的变化（或增或减）单位大小是 \(1\)。
因此，我们最后的值一定是至多 \(2\) 个连续整数区间：

• 一个是由 \(0\)（空区间） 扩展而来，并且扩展出的区间不包含 \(x\)。
• 一个是由 \(a_x\) 扩展而来。

首先考虑第一种区间，我们求出不包含 \(x\) 的所有区间和的最大值和最小值即可。
这个很明显是一个区间最值问题，但是这里涉及到区间和，所以我们先把原数组 \(a\) 进行前缀和操作转化为前缀和数组 \(pre\)。
然后，我们把前缀和数组 \(pre\) 存入 线段树 或 ST表 中维护区间前缀和最大值和最小值。
对于 \(x\) 左边的区间，我们从左到右枚举区间的左端点 \(i\)，查询 \(i\) 到 \(x\) 的区间前缀和最大值，减掉 \(pre_{i - 1}\)，就可以得到以 \(i\) 作为左端点的不包含 \(x\) 的所有区间的最大区间和。最小区间和同理。
对于 \(x\) 右边的区间，我们从左到右枚举区间的左端点 \(i\)，查询 \(i\) 到 \(n\) 的区间前缀和最大值，减掉 \(pre_{i - 1}\)，就可以得到以 \(i\) 作为左端点的不包含 \(x\) 的所有区间的最大区间和。最小区间和同理。
对于此类区间得到的结果取个并集，就是此类区间最后的结果。

然后是第二种区间，由 \(a_{x}\) 扩展而来。
此时这个区间一定包含 \(x\) ，因此，我们只需要以 \(x\) 为起点，分别向左向右扩展。
向左扩展变化的最小值加上向右扩展变化的最小值，就是此类区间的最小区间和。
向左扩展变化的最大值加上向右扩展变化的最大值，就是此类区间的最大区间和。

最后对两种区间求得的结果再取一个并集即可。

时间复杂度：\(O(n \log n)\)。

AC CODE

// Problem: C. Sums on Segments
// Contest: Codeforces - Educational Codeforces Round 173 (Rated for Div. 2)
// URL: https://codeforces.com/contest/2043/problem/C
// Memory Limit: 256 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
#define int long long
#define inf 2e18
#define ull unsigned long long
#define ls o << 1
#define rs o << 1 | 1using namespace std;const int N = 2e5 + 9;
int a[N];
int tmx[N << 2], tmi[N << 2];
int n;//线段树维护区间最值
void pushup(int o)
{tmx[o] = max(tmx[ls], tmx[rs]);tmi[o] = min(tmi[ls], tmi[rs]);	
}void build(int s = 1, int e = n, int o = 1)
{if(s == e)return tmx[o] = a[s], tmi[o] = a[s], void();int mid = s + e >> 1;build(s, mid, ls);build(mid + 1, e, rs);pushup(o);
}int querymx(int l, int r, int s = 1, int e = n, int o = 1)
{if(l <= s && e <= r) {return tmx[o];}int mid = s + e >> 1;int res = -inf;if(mid >= l)res = max(res, querymx(l, r, s, mid, ls));if(mid + 1 <= r)res = max(res, querymx(l, r, mid + 1, e, rs));return res;
}int querymi(int l, int r, int s = 1, int e = n, int o = 1)
{if(l <= s && e <= r) {return tmi[o];}int mid = s + e >> 1;int res = inf;if(mid >= l)res = min(res, querymi(l, r, s, mid, ls));if(mid + 1 <= r)res = min(res, querymi(l, r, mid + 1, e, rs));return res;
}void solve()
{cin >> n;for(int i = 1;i <= n;i ++)cin >> a[i];int ix = -1;for(int i = 1;i <= n;i ++)if(abs(a[i]) != 1)ix = i;for(int i = 1;i <= n;i ++)//前缀和a[i] += a[i - 1];build();//构建线段树if(ix == -1)ix = n + 1;int nomi = 0, nomx = 0;//第一类区间for(int i = 1;i <= n;i ++) {if(i == ix)continue;if(i <= ix) {nomi = min(nomi, querymi(i, ix - 1) - a[i - 1]);nomx = max(nomx, querymx(i, ix - 1) - a[i - 1]);} else {nomi = min(nomi, querymi(i, n) - a[i - 1]);nomx = max(nomx, querymx(i, n) - a[i - 1]);}}//第二类区间int hasmi = 0, hasmx = 0;if(ix <= n) {hasmi = a[ix] - a[ix - 1];hasmx = a[ix] - a[ix - 1]; int lmi = 0, lmx = 0;int rmi = 0, rmx = 0;int now = 0;for(int i = ix - 1;i;i --) {now += a[i] - a[i - 1];lmi = min(lmi, now);lmx = max(lmx, now);}now = 0;for(int i = ix + 1;i <= n;i ++) {now += a[i] - a[i - 1];rmi = min(rmi, now);rmx = max(rmx, now);}hasmi = hasmi + lmi + rmi;hasmx = hasmx + lmx + rmx;} set<int> ans;for(int i = nomi;i <= nomx;i ++)ans.insert(i);for(int i = hasmi;i <= hasmx;i ++)ans.insert(i);cout << ans.size() << '\n';for(auto &i : ans)cout << i << ' ';cout << '\n';
}signed main()
{ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int t = 1;cin >> t;while(t --)solve();return 0;
}