暴力:每一件物品其实只有两个状态,取或者不取,所以可以使用回溯法搜索出所有的情况,那么时间复杂度就是O(2^n),这里的n表示物品数量。
所以暴力的解法是指数级别的时间复杂度。进而才需要动态规划的解法来进行优化!
二维dp数组01背包
-
确定dp数组及下标含义
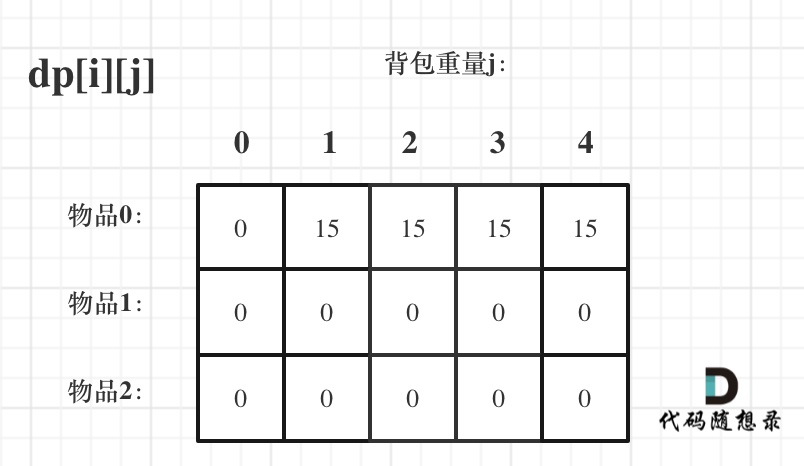
dp[i][j]表示前i件物品恰放入一个容量为j的背包可以获得的最大价值。
此时最后返回dp[n-1][w]即可 -
确定递推公式
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
解释:从“不放入第i件物品”与“放入第i件物品的价值 + 放入前i-1件物品到容量为j-weight[i]的背包可获得的最大价值”中选最大值 -
dp数组初始化
- 容量为0时,都为0
- 因为dp[i][j]需要用到dp[i-1][j],所以需要初始化第一行。
当j>=weight[0]时,dp[0][j]应该是value[0];否则是0.
关于初始化,一定要和dp数组的定义吻合,否则到递推公式的时候就会越来越乱。
- 确定遍历顺序
先遍历物品再遍历容量 或相反都可以。因为递推公式用到的都是dp[i][j]左上的元素。
代码
#include<iostream>
#include<vector>using namespace std;int main(){int M,N;cin>>M>>N;vector<int> value(M);vector<int> cost(M);for(int i=0;i<M;i++){cin>>cost[i];}for(int i=0;i<M;i++){cin>>value[i];}vector<vector<int>> dp(M,vector<int>(N+1,0));//dp[M][N]是从0到M-1个材料中选择,容量为N时的最大价值//初始化for(int j=cost[0];j<=N;j++){dp[0][j] = value[0];}for(int i=1;i<M;i++){for(int j=0;j<=N;j++){if(j<cost[i])dp[i][j] = dp[i-1][j];else dp[i][j] = max(dp[i-1][j],dp[i-1][j-cost[i]]+value[i]);}}cout<< dp[M-1][N];return 0;
}
一维dp数组01背包
二维递推公式dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
发现如果把dp[i - 1]那一层拷贝到dp[i]上,表达式完全可以是:dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);
区别在于遍历顺序。
- 容量只能从大到小遍历。
如果从小到大,上一层的dp[j]会被覆盖,导致后续计算dp[i][j-weight[i]]时使用的是这一层的dp而出现错误。如果从大到小遍历,因为递推公式不会用到 - 只能先遍历物品再遍历容量
因为容量从大到小遍历,如果先遍历容量再遍历物品。算不出答案。
#include<iostream>
#include<vector>using namespace std;int main(){int M,N;cin>>M>>N;vector<int> value(M);vector<int> cost(M);for(int i=0;i<M;i++){cin>>cost[i];}for(int i=0;i<M;i++){cin>>value[i];}// 一维数组vector<int> dp(N+1,0);//初始化for(int j=cost[0];j<=N;j++){dp[j] = value[0];}//遍历顺序——容量从后往前for(int i=1;i<M;i++){for(int j=N;j>=cost[i];j--){dp[j] = max(dp[j],dp[j-cost[i]]+ value[i]);}}cout << dp[N];return 0;
}