最早发明的自平衡二叉树：AVL-编程知识

最早发明的自平衡二叉树：AVL

news/2025/1/1 16:09:42/文章来源:https://www.cnblogs.com/fush/p/18639442

前言

更好的阅读体验
默认读者会基本的 BST 操作。

节点定义

平衡因子：BF(BalanceFactor)，左子树高 \(-\) 右子树高。
平衡树是让树的形态尽可能像完全二叉树，而不是链。

在 AVL 中，我们认为 \(\left|\text{BF}\right|\le 1\)，也就是 BF 为 \(0,1,-1\) 时的子树是平衡的，否则就是不平衡的。

struct node{int ch[2], size, val, h;//h 是树高  
}d[N];
int root, tot;
#define ls(x) d[x].ch[0]  
#define rs(x) d[x].ch[1]  
#define getBF(x) (d[ls(x)].h - d[rs(x)].h)//计算平衡因子

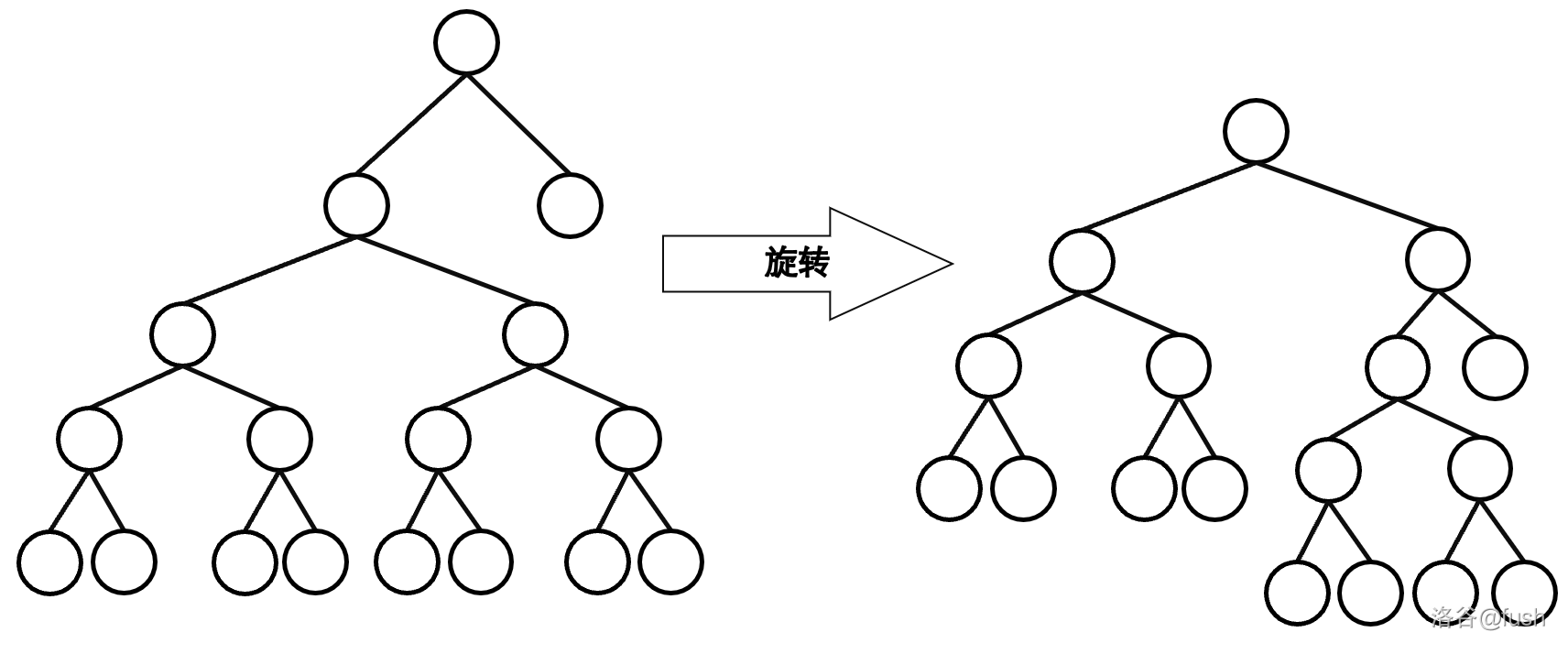
旋转

rotate 操作是把某个给定节点上移一个位置，并保证二叉搜索树的性质不改变。
旋转操作分为左旋和右旋（图上节点是编号）。

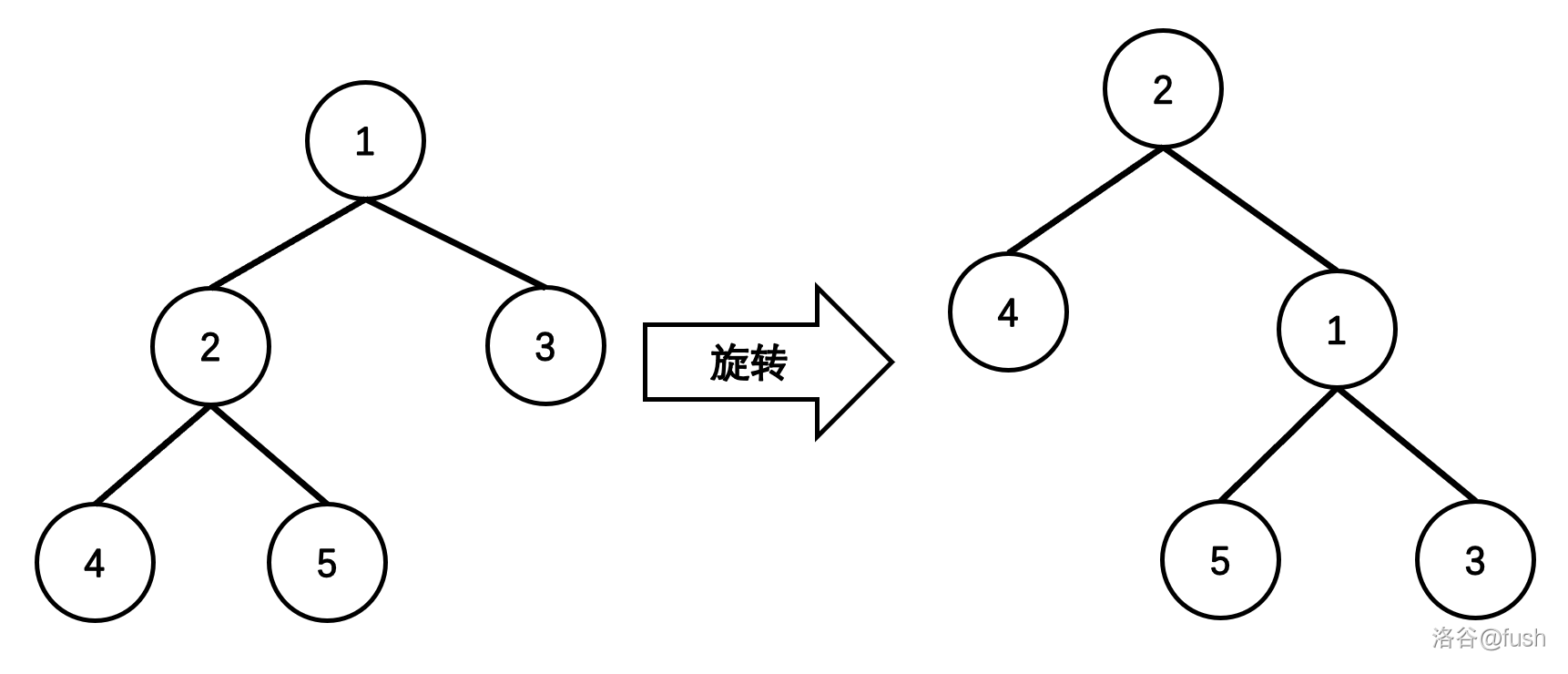
我们来模拟一下右旋的操作（红色是要删除的，蓝色是更改后的）。

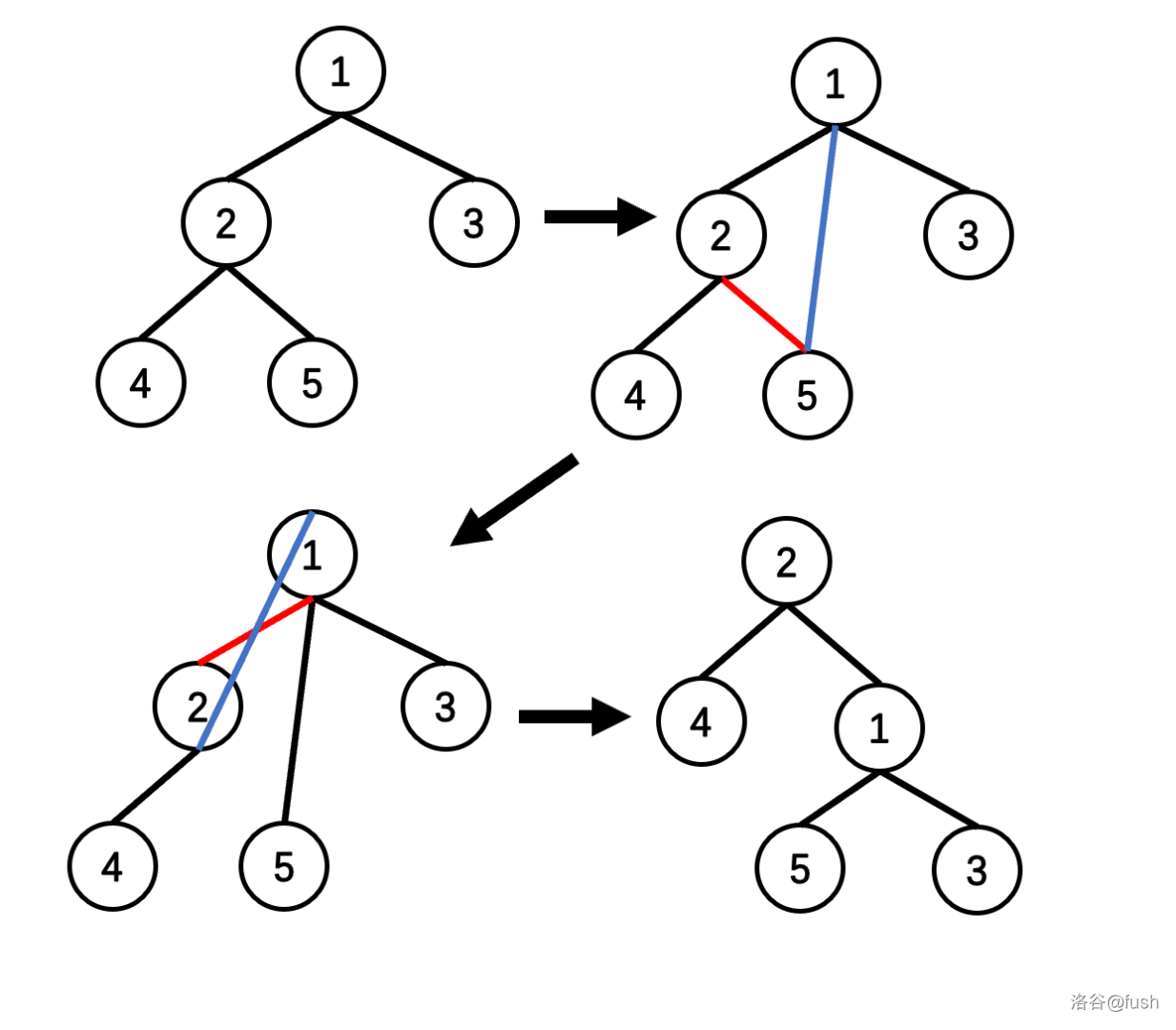
这样就完成了一次旋转。
而在实现中，我会把左右旋写在一起。
这里的 rotate(x,0) 表示将 \(x\) 的左儿子提到 \(x\) 的高度。
这里的 rotate(x,1) 表示将 \(x\) 的右儿子提到 \(x\) 的高度。

void rotate(int&now, int dir){int t = d[now].ch[dir];d[now].ch[dir] = d[t].ch[!dir];d[t].ch[!dir] = now;pushup(now), pushup(t), now = t;
}

平衡维护

如果它是平衡的，那么我们更新节点。
否则，我们考虑左子树过高的情况（右儿子同理），即 \(BF > 1\)：
我们又两种可能：
左儿子的左子树较高（图中的数字是树高）：

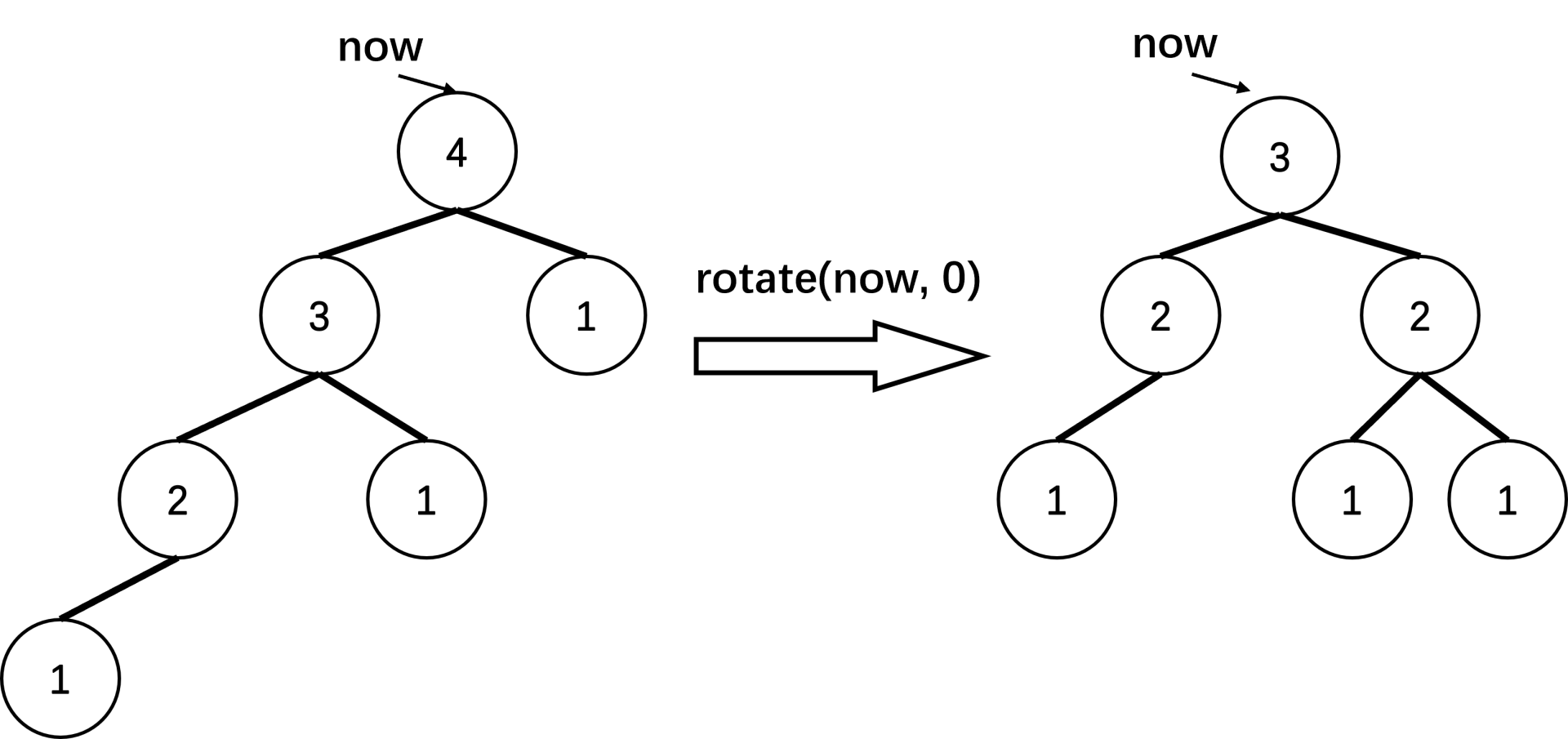
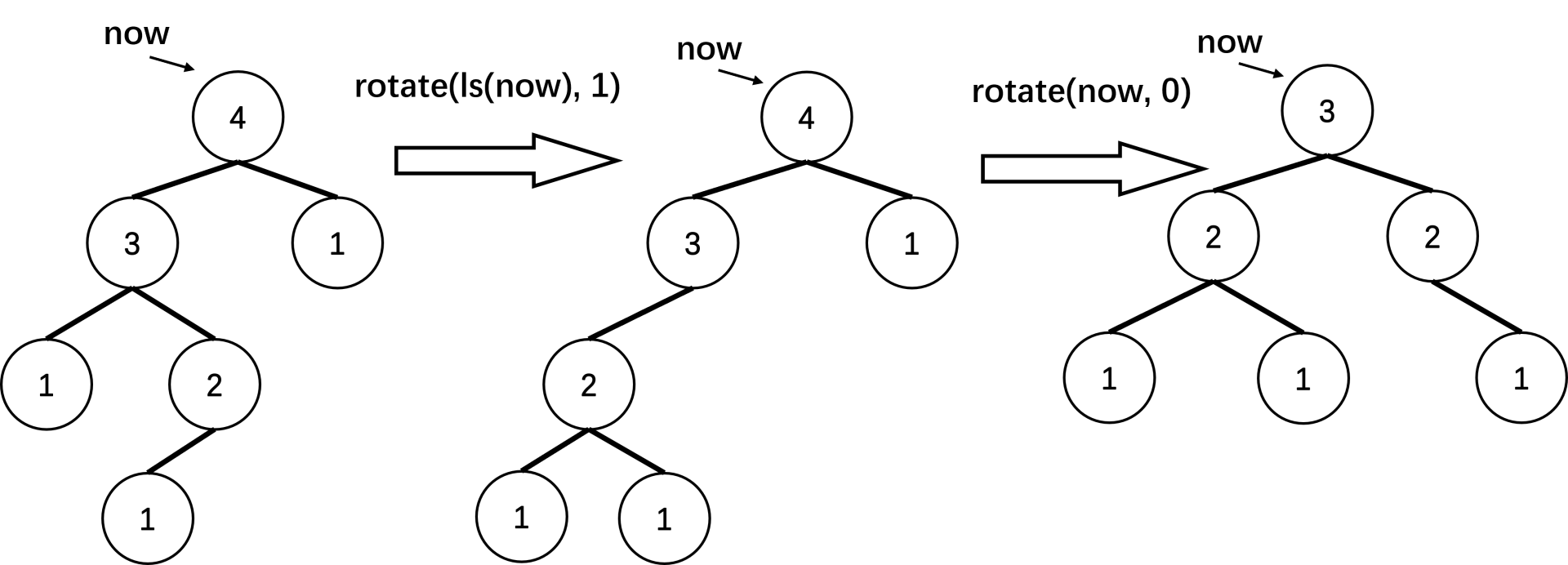
左儿子的右子树较高：
我们先转换成第一种，再平衡。

void maintain(int&x){//引用  int BF = getBF(x);if(BF > 1){if(getBF(ls(x)) <= 0)rotate(ls(x), 1);//转换成第一种。  rotate(x, 0);}else if(BF < -1)(getBF(rs(x)) >= 0) && (rotate(rs(x), 0), 1), rotate(x, 1);	  else if(x)pushup(x);
}

插入

这里我们递归插入，然后在返回时维护平衡即可。

void insert(int&now, int val){if(!now)return void(now = newnode(val));//空节点  if(d[now].val < val)insert(rs(now), val);else insert(ls(now), val);maintain(now);//维护平衡  
}

删除

如果删除节点最多有一个儿子，那么我们用它的儿子顶替它。
否则和后继交换。

记得在返回时维护。

void del(int&now, int val){if(!now)return;if(d[now].val == val){int w = now;if(ls(now) && (w = rs(now))){//和后继交换，并删除后继  while(ls(w))w = ls(w);d[now].val = d[w].val, del(rs(now), d[w].val);}else now = ls(now) ? ls(now) : rs(now);//和儿子交换  }else if(d[now].val < val)del(rs(now), val);else del(ls(now), val);maintain(now);
}