1.2 可压缩流:激波和膨胀扇
前言
欢迎观看《Bang Dream! Ave mujica》,一部超好看的少女乐队动漫,从2025.1.2开始,每周四晚10点更新。
哇嘎利马斯
大量玩梗注意
AA笔记主要参考刘永学主编《空气动力学》,讲的物理概念很清晰易懂,推荐给大家。
扰动的传播
接下来我们讨论扰动的传播(proppagation of disturbances)。
考虑一个平静的湖面。如果我们往湖面丢一个石头,会发生什么?
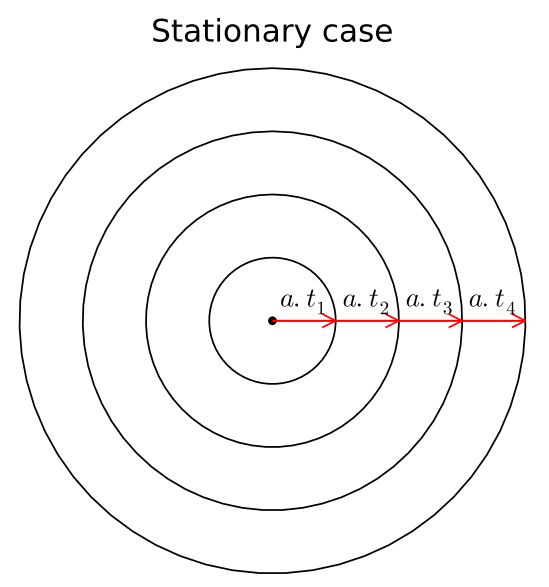
就像这样,以我们丢的石头入水的点为中心,水波等速地向周围传播。
这就是扰动在流体中传播的机制,当然是对于固定来源而言。
类比到空气中,我们可以想到声音在空气中的传播,而来源是固定源,比如说我在固定点大吼一声 (你敢答应吗?) 。
如上图所示,令a等于声速,扰动波在时间\(\delta t\)内,传播距离为\(\delta x = a \delta t\)。
但是,如果我一边持续地运动 (扑向图书馆) ,一边 (因为赶毕设过于折磨而) 持续地发出 (“尖锐的爆鸣”) 声音呢?
这就要分成两种情况了。
-
源的运动速度为亚音速(subsonic):
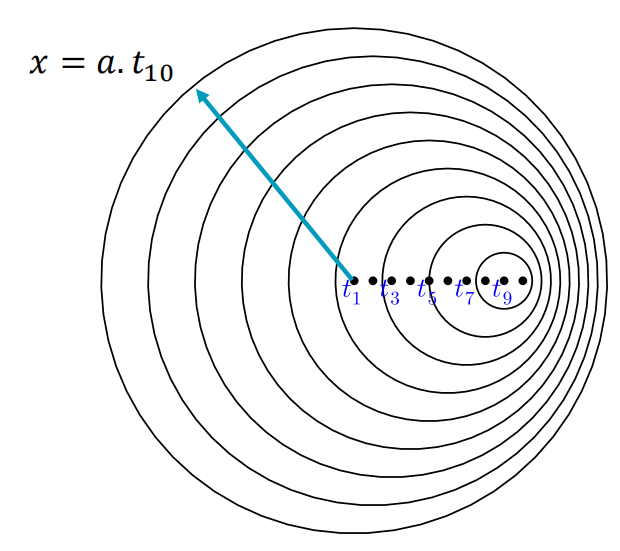
在每个时刻,扰动源会产生一个新的扰动波(压力波),以声速a向外传播。
每个圆圈代表在不同时刻t产生的扰动波,表明在当前时间(这里是\(t_{10}\))波已经传播了多远。
关键特征:
- 扰动源始终位于波前内部,由于扰动源的移动速度小于扰动波的传递速度;
- 由于扰动源的移动,扰动波的分布是不对称的,其中在扰动源前进的方向上,波前之间的距离更近(波长更短);在扰动源后方,波前之间的距离更远(波长更长)。
-
源以超音速(supersonic)运动:
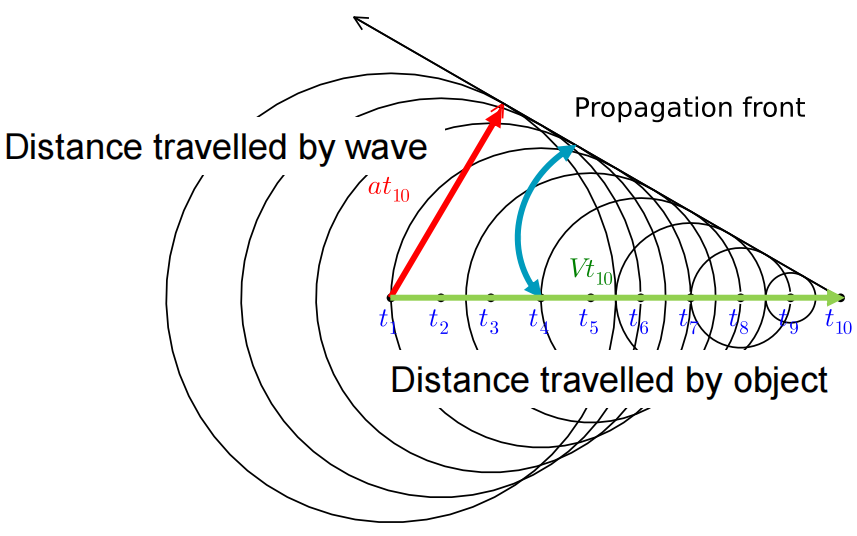
在我(扰动源)以超音速前进的并同时发出声音的情况下,我比其他的扰动波啊,跑得还快(也就是扰动源的速度比声速快)。
这样,扰动源就会追上之前发出的扰动波。
这些扰动波互相叠加、干涉,形成一个明显的波前(wave front,或propagation front),在图中表现为包络线(envelope,在每个切点处都与该系列曲线中的一条相切),包裹着这组扰动波。
在三维空间中,这两个波前实际上构成了一个以我为顶点的锥体,称为音锥。
这就是超音速飞机能在它发出的声音被听到之前到达一个位置的原理。
我们可以轻松地计算波前包络线与扰动源运动轨迹线之间的夹角,定义为马赫角\(\mu\):
\[\begin{equation}\begin{aligned} \sin\mu&=\frac{at}{Vt}=\frac{a}{V}=\frac{1}{M} \\\mu&=\sin^{-1}\left(\frac{1}{M}\right) \end{aligned} \end{equation} \]
激波的不同类型
弓形激波
当一个物体以超音速在空气中运动时,如果物体的头部比较钝(blunt),就会在物体前方形成一道弯曲的激波,称为弓形激波(bow shock)。
- 激波是不可逆过程,会产生熵增,导致总压下降;
- 弓形激波是由正激波和一系列弱激波连续变化组合而成的,其中心部分接近正激波,正激波的压力损失比斜激波更大。
因而弓形激波会导致很大的压力损失。

但在航天器再入大气层时,弓形激波是有利的,因为:
- 压力损失大,意味着动能损失大,有助于航天器减速;
- 弓形激波把航天器和高温气流隔离,包括激波后的亚音速流动区、激波和航天器之间的间隙,可以起到一定的热防护作用。
正激波
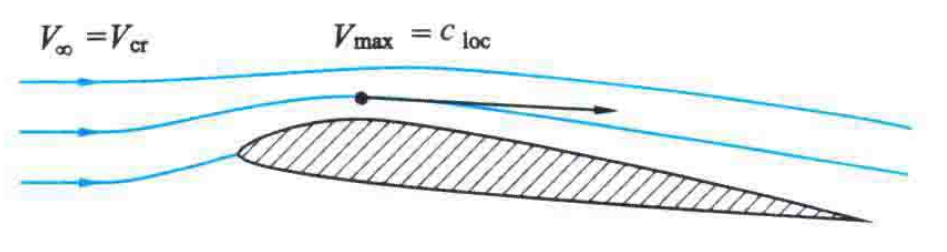
当飞机在高亚音速飞行时,空气流过翼型上表面凸起的地方,由于流管收缩,局部流速加快,又引起局部温度降低,从而使得局部音速减小。
当飞行速度增大时,上表面最低压力点的气流速度不断增大、局部音速不断减小。
-
当飞行速度增大到一定程度,机翼表面最低压力点的气流速度等于该点的声速,该点称为等声速点,此时的飞行速度称为临界速度\(V_{ct}\),临界速度与该飞行高度的声速之比为临界马赫数\(Ma_{cr}=\frac{V_{cr}}{c}\)。
-
当飞行马赫数>临界马赫数时,等声速点后面,流管扩展,空气膨胀加速,出现局部超音速区。
在该区域内,压力比大气压力小很多,但翼型后缘处的压力却接近大气压,存在一个较大的逆压梯度。
这种逆压梯度使得局部超音速气流受到阻挡,产生较强的压力波,压力波逆翼型表面的气流向前传播。
-
该强压力波的传播速度大于当地声速,又因为超声速区域内的气流速度大于局部音速,因此,当压力波传到某一位置,传播速度等于迎面的局部超音速气流速度时,就不能继续向前传播了。
结果,该压力波相对于翼型,稳定在这一位置上,于是翼型上表面出现一个压力突增的分界面,就是局部(正)激波。
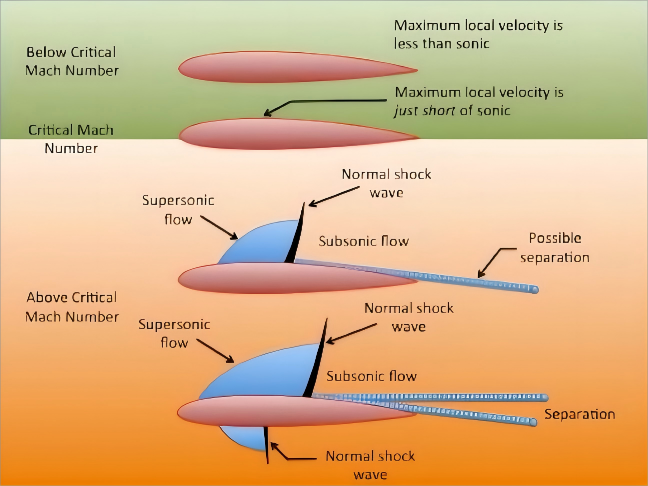
气流通过局部激波后,减速为亚音速气流;波后压力、温度、密度突然升高。
接下来用公式描述翼型局部正激波前后的压强、密度、温度、马赫数关系:
-
压强:
\[\begin{equation}\frac{p_2}{p_1}=\frac{2\gamma M_1^2-(\gamma-1)}{\gamma+1} \end{equation} \] -
密度:
\[\begin{equation}\frac{\rho_2}{\rho_1}=\frac{(\gamma+1)M_1^2}{2+(\gamma-1)M_1^2} \end{equation} \] -
温度:
\[\begin{equation}\frac{T_2}{T_1}=\frac{p_2}{p_1}\frac{\rho_1}{\rho_2} \end{equation} \] -
马赫数:
\[\begin{equation}M_2^2=\frac{(\gamma-1)M_1^2+2}{2\gamma M_1^2-(\gamma-1)} \end{equation} \]
根据上述公式,可以绘制下面的图像:

该图象中:
-
下游马赫数:
无论上游马赫数\(M_1\)是多少,激波后马赫数undefined;
当\(M_1\)达到高超音速范围时(大于5),\(M_2\)从0.4开始趋于平缓(flatten)。
-
总压比:
\(\frac{p_{0,~2}}{p_{0,~1}}<1\),气流经过正激波后的总压下降,表明穿过激波的流动有能量损失,激波过程是不可逆、非等熵的;
随着\(M_1\)增加,总压比迅速下降,当\(M_1=5\)(高超音速)时,总压损失达到95%,意味着很大一部分动能转化为了内能,并以热量形式耗散掉了,这就是高超音速飞行器需要考虑严重的气动加热问题的原因。
此外,总压的大幅损失也意味着存在很大的阻力。
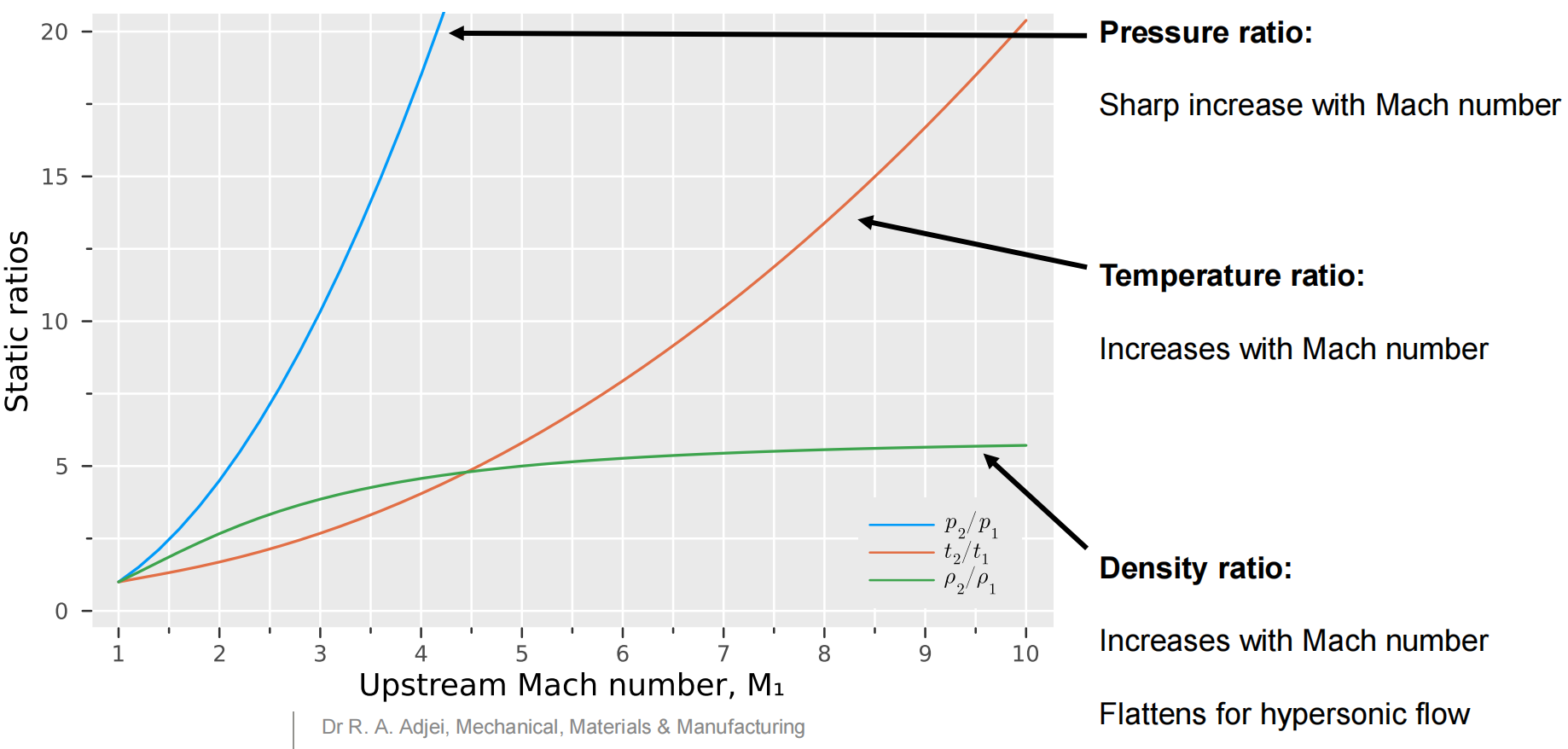
这个图中:
- 静压:气流经过正激波后,静压显著上升,且上游马赫数越大,静压升高幅度越大;
- 温度比:气流经过正激波后,温度升高,且上游马赫数越大,温度升高幅度越大;
- 密度比:气流经过正激波后,密度升高,但增长逐渐平缓,在高超音速范围内趋于一个极限值。
正激波的性质:
- 下游流动亚音速;
- 不等熵流动;
- 穿过正激波后,流动总压降低;
- 绝热流动(局部正激波很薄,过程很快,没有时间进行显著的热交换);
- 对于稳定的正激波,前后总温度(流体等熵地减速到静止状态所能达到的温度)保持不变,即总能量不变。
斜激波
原理
空气受到压缩扰动有两种情形:
- 超音速气流受到物面阻挡,包括向内转折和正面阻挡;
- 逆压影响(上面讲过了)。
超音速气流流过向内转折的凹角将产生激波。
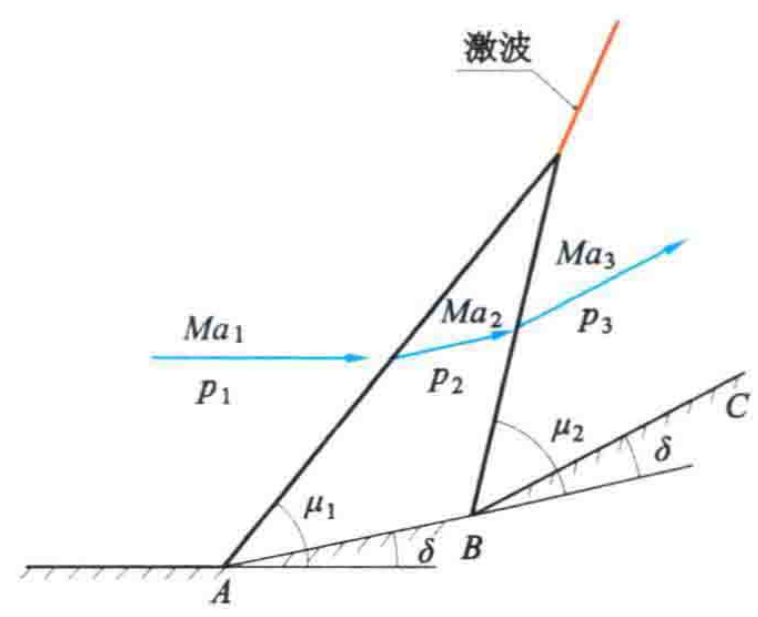
如果折角\(\delta\)无限微小,凹角的顶点A对气流产生弱的压缩扰动,扰动的界限波为弱压缩波。
如果物面有两个连续微小转折,则将产生两道弱压缩波。
由于压缩波后,气流速度与马赫数降低,后一道弱压缩波的马赫角,将大于前一道弱压缩波的马赫角。
因此,这两道波必然在气流中的某一处相角,形成压缩强度增大的波。
如果转折点很多,则最后形成的压缩波强度必然很大,这就是激波。
如果这些转折点无限接近,结果会形成一个有限大的转折角,激波将出现在这个转折角的顶点。这就是斜激波(oblique shock) 。
这说明:激波是无数的弱压缩波的叠加。
物理性质
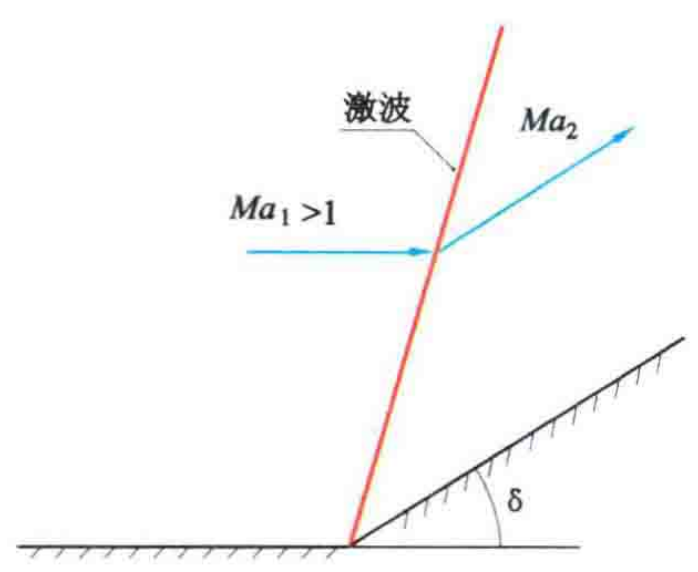
我们定义如下图所示的符号和物理性质:
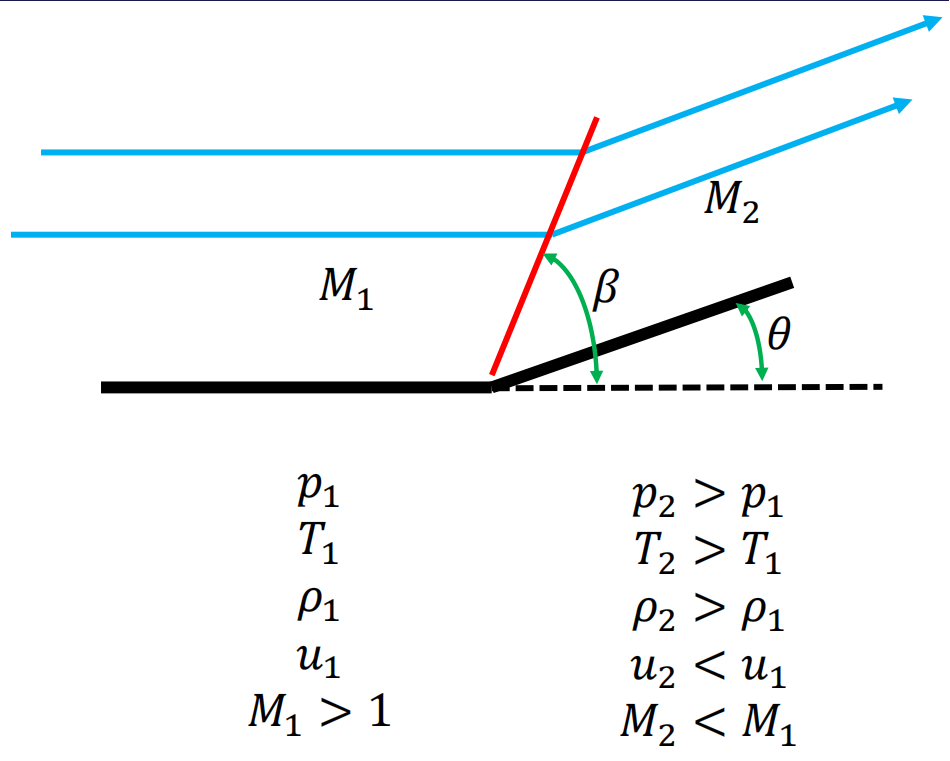
定义偏转角(deflection angle)\(\theta\),波角(wave angle)\(\beta\)。其余定义参见上图。
斜激波的物理性质:
- 没有热的“添加”,即绝热(adiabatic)过程,这样总的温度和焓不变;
- 流动是非等熵、不可逆的,因此熵增加,并且可观察到总压的损失;
- 静态属性(压强、密度、温度)几乎瞬间增加,因为激波很薄;
- 垂直方向的特性与正激波相同;激波前后切向速度/马赫数相同。
把斜激波分解成如下图所示的模型:
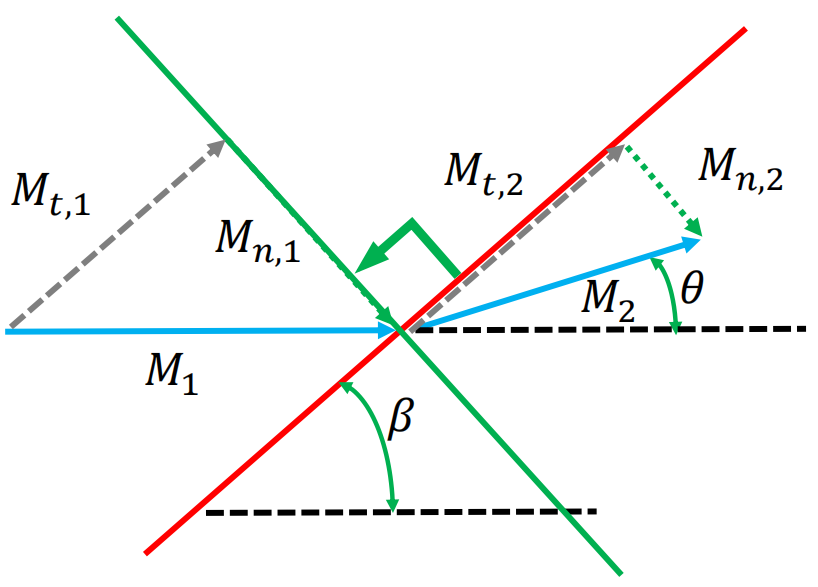
图中,蓝色线是几何偏转角,红色线是激波。
这里把斜激波前后的流动速度,分解为垂直于激波和平行于激波的两个分量。
其中,平行于激波的分量(或切向分量)在经过斜激波时不变,无需考虑,因而我们主要考虑法向分量。
流动的法向分量也可以看做是一个正激波,\(M_{n,~1}\)和\(M_{n,~2}\)之间也遵循正激波关系。
引入如下两个公式:
构建物理量关系:
-
压强:
\[\begin{equation}\frac{p_2}{p_1}=\frac{2\gamma M_{n,1}^2-(\gamma-1)}{\gamma+1} \end{equation} \] -
密度:
\[\begin{equation}\frac{\rho_2}{\rho_1}=\frac{(\gamma+1)M_{n,1}^2}{2+(\gamma-1)M_{n,1}^2} \end{equation} \] -
温度:
\[\begin{equation}\frac{T_2}{T_1}=\frac{p_2}{p_1}\frac{\rho_1}{\rho_2} \end{equation} \] -
马赫数:
\[\begin{equation}M_{n,2}^2=\frac{(\gamma-1)M_{n,1}^2+2}{2\gamma M_{n,1}^2-(\gamma-1)} \end{equation} \]
注意到上述公式的构成与正激波完全相同。
\(\theta - \beta - M\)关系
我们可以建立马赫数M、几何偏转角\(\beta\)、激波角\(\theta\)之间的关系。
上式的推导可在刘沛清《空气动力学》第7章第9节找到,这里不再赘述,有兴趣的同学可以自行寻找。
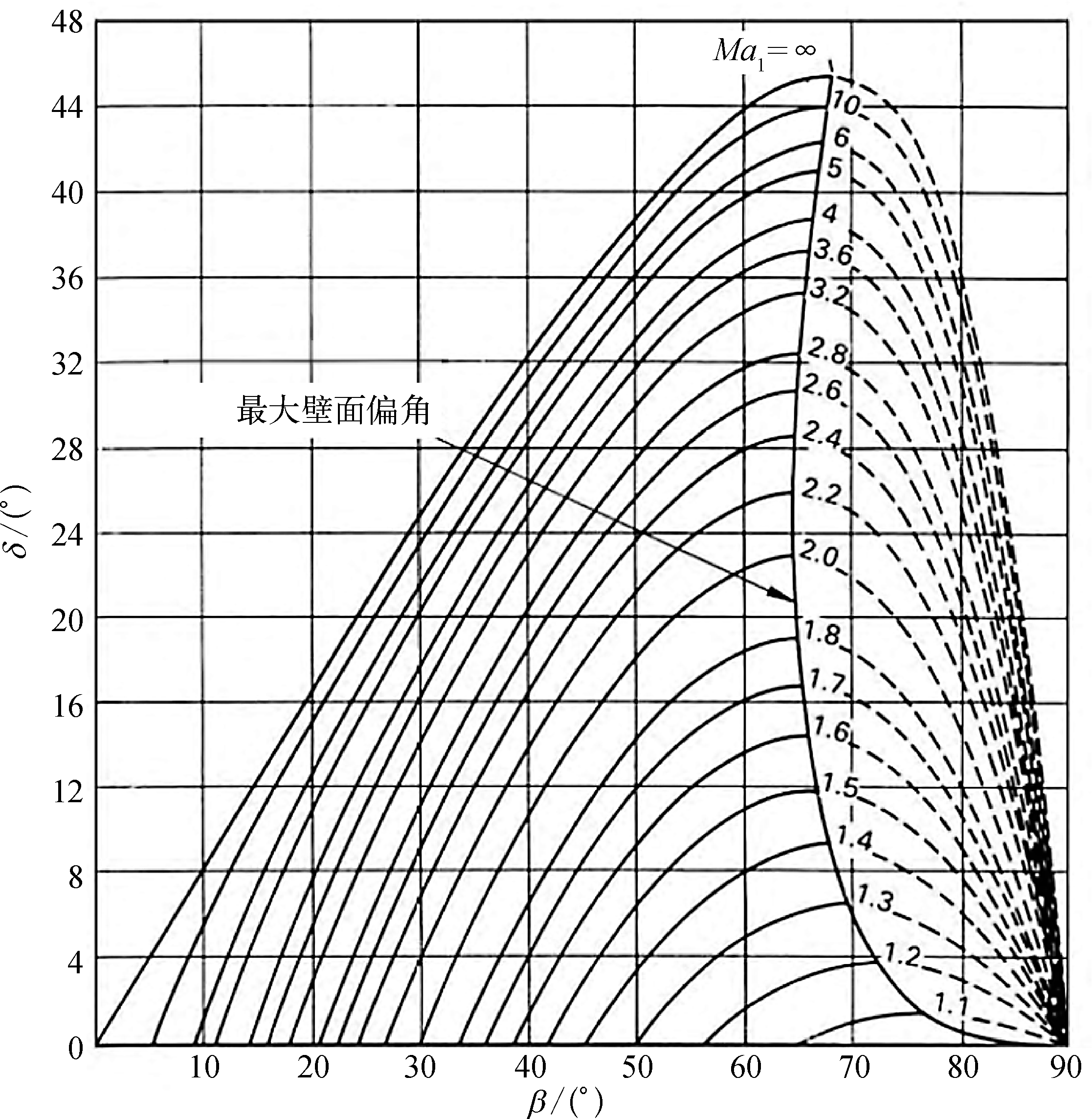
(这个图中的\(\delta\)就是流线偏转角\(\theta\))
可以从上式解读出以下信息:
-
对于给定\(M_1\)和\(\theta\),都有两个不同的\(\beta\)存在,分别对应强激波和弱激波。
弱激波:\(\beta\)较小,对应激波强度较弱,激波后的马赫数\(M_2\)相对较大,但仍然小于1;
强激波:\(\beta\)较大,对应激波强度更强,激波后的马赫数\(M_2\)相对较小,总压损失相对更大。
-
当流线偏转角\(\theta = 0\)时,存在两个激波角\(\beta\)的解:
- \(\beta = \mu\),即马赫角,对应一个无限弱的激波,即马赫波,不改变气流流动方向、不引起任何参数变化;
- \(\beta = 90^{\circ}\),对应正激波,垂直于来流方向。
-
对于给定的\(M_1\),存在一个最大偏转角\(\theta_{max}\)。
当激波角\(\beta\)从马赫角\(\mu\),逐渐增大到\(90^{\circ}\)的过程中,\(\beta\)先增加到一个最大值\(\beta_{max}\),然后再减小到0,即正激波。
当\(\theta < \theta_{max}\)时,存在两个\(\beta\)解;
当\(\theta = \theta_{max}\)时,只有一个\(\beta\)存在;
当\(\theta > \theta_{max}\)时,方程无解,无法形成附体斜激波,会形成脱体激波。
-
由于弱激波的熵增较小,能量损失较小,符合自然界中能量损失最小化的趋势,因而实际流动中,通常观察到的是弱激波。
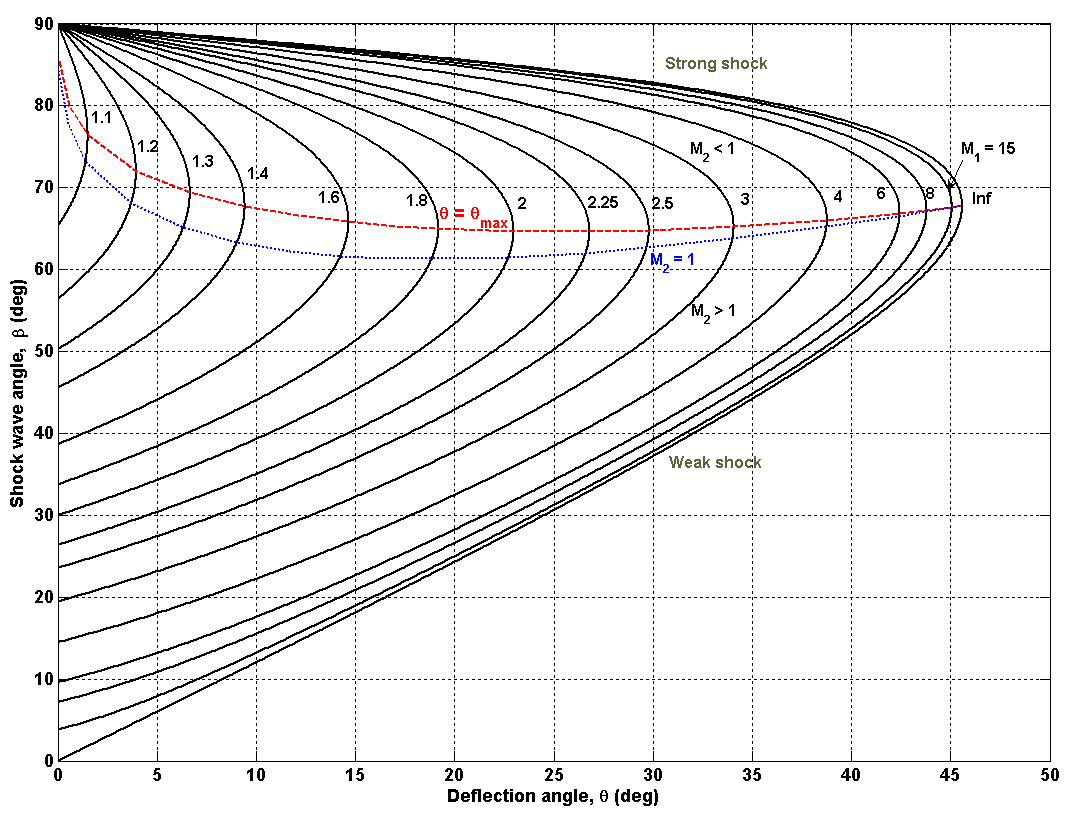
进一步观察上图,可得如下结论:
- 红线标明了禁止脱体激波形成的范围;
- 蓝线约束了弱激波的生成,因为弱激波不会把流速降低到亚音速,而强激波后的流动始终是亚音速的。
膨胀扇
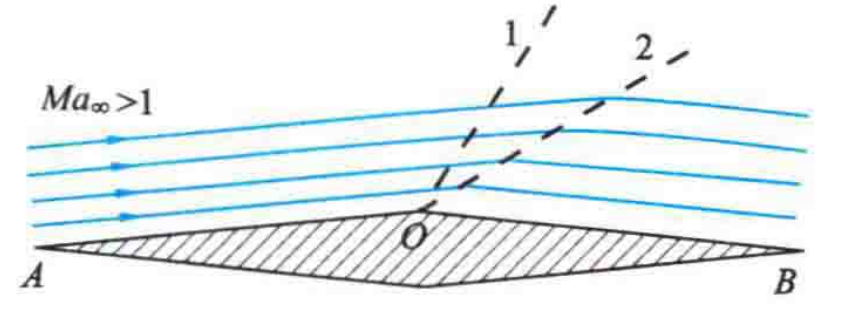
如上图,AOB是一个向外转折的物体表面,称为外凸角。空气首先以超音速沿表面AO段平行流动。
空气流动到转折点O时,因为表面转折,流动空间扩大,气流膨胀加速,引起压力逐渐降低。
这种扰动从转折点O向外传播,但其传播范围仅限于弱扰动边界波(图中O1)后。
气流\(M\)数越大,弱扰动边界波越向后倾斜。
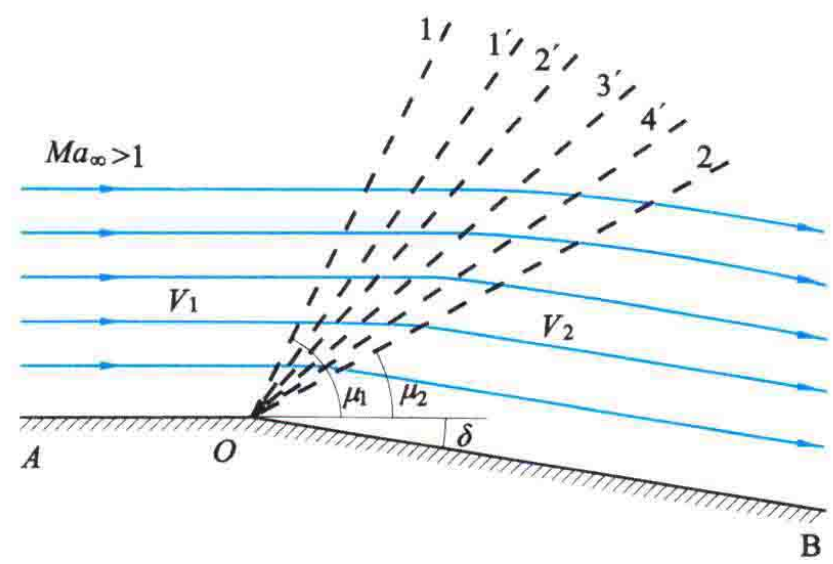
气流通过波面O1,流速稍有加快,压力、密度、温度稍有降低,气流方向稍微向表面OB段靠拢,但还没有完全平行。
而流速加快,使得从O发出的另一条弱扰动边界波O1'更向后倾斜一点。
依此类推,直到气流通过弱扰动边界波O2,气流方向与表面OB段平行,而不再偏转,空气以超音速\(V_2\),沿着平行于表面OB段的方向流动。
所以,弱扰动边界波O1和O2之间所夹的扇形区域,就是超音速气流不断膨胀、加速的范围。
上述弱扰动边界波就称为膨胀波,扇形区域称为膨胀扇(expansion fan)。
可以构建外折角(\(\theta\)或\(\delta\),我们上课用\(\theta\))和来流马赫数之间的关系,称为普朗特-迈耶尔流动(Prandtl-Meyer flow):
对于膨胀波,流动是等熵的,因此直接用等熵流动关系求温度、压强和密度比即可。