这场比赛排名第 1 - 1000 名的参赛者 可获「NIO 蔚来」简历内推机会，比有的场次前十才给容易多了。

2833. 距离原点最远的点

距离原点最远的点

注意是移动n次后，不是移动过程中。
可以分为最靠左的点和最靠右的点，就是把_都换成L或R。
然后计算左右的差，求绝对值。
O(n)

class Solution {
public:int furthestDistanceFromOrigin(string moves) {int LCnt = 0;int RCnt = 0;int allCnt = 0;int ans = 0;for(int i=0;i<(int)moves.length();i++){if(moves[i]=='L'){LCnt++;}else if(moves[i]=='R'){RCnt++;}else{allCnt++;}}ans = max(ans, max(abs(LCnt+allCnt-RCnt),abs(RCnt+allCnt-LCnt)));return ans;}
};

2834. 找出美丽数组的最小和

找出美丽数组的最小和

每一对和为目标值的两个数只能选一个，显然应该选小的。
所以简单起见从1开始枚举，检查和之前的值和不为目标值，用哈希表记录。
O(n)

class Solution {
public:long long minimumPossibleSum(int n, int target) {unordered_set<int> st;long long ans = 0;int now = 1;for(int i=1;i<=n;i++){while(st.count(target-now)){++now;}st.insert(now);ans+=now;++now;}return ans;}
};

2835. 使子序列的和等于目标的最少操作次数

使子序列的和等于目标的最少操作次数

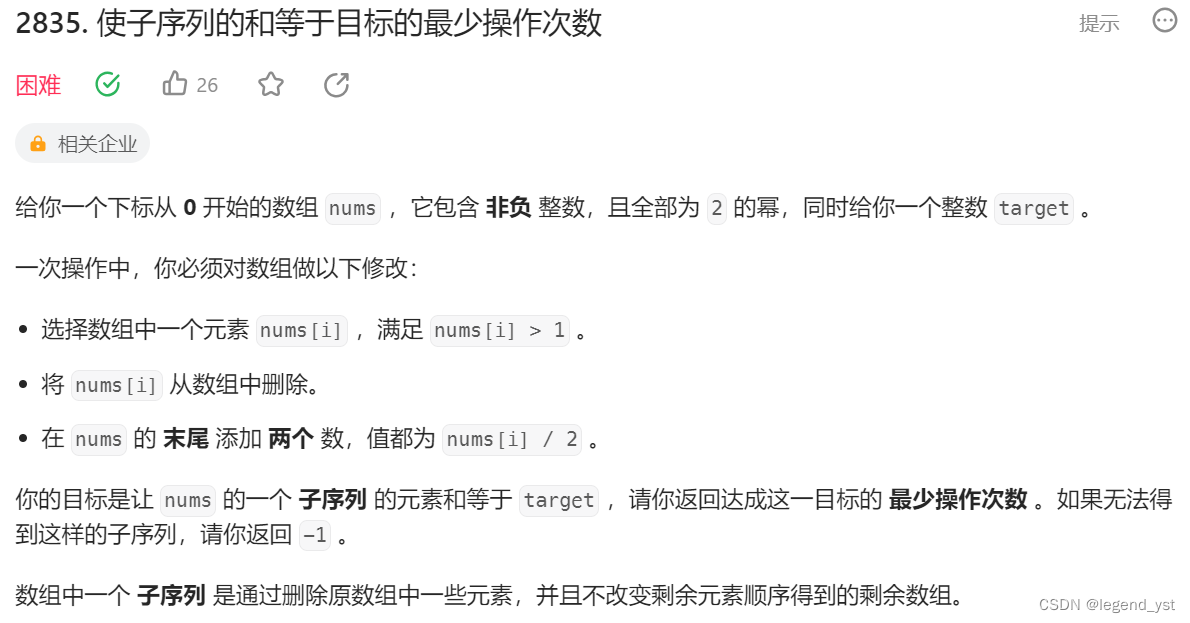
以2为底取对数，记录每种2的幂的个数。
对于target中的每个为1的二进制位，要么用1个对应位nums中的数，要么用多个低位的数加起来，实在不行从高位借位（记录成本）。
最后检查最高位是否存在借不到的情况，输出-1。
O(n)

class Solution {
public:int minOperations(vector<int>& nums, int target) {unordered_map<int,int> mp;for(int i=0;i<=30;i++){mp[1<<i] = i;}int a[50] = {};for(const auto&v: nums){++a[mp[v]];}int b[50] = {};int ans = 0;for(int i=0;i<=30;i++){if(target&(1<<i)){b[i] = b[i]+a[i]-1;}else{b[i] = b[i]+a[i];}if(b[i]<0){//cout<<"! " <<i<<endl;ans+=(-b[i]+1)/2;b[i+1]-=(-b[i]+1)/2;b[i] = (-b[i])%2;}else if(b[i]>0){b[i+1] += b[i]/2;b[i]%=2;}//if(b[i])cout<<"i "<<i<<" "<<b[i]<<endl;}if(b[31]<0){return -1;}return ans;}
};

TODO 2836. 在传球游戏中最大化函数值

在传球游戏中最大化函数值

想出最优的正解了，但是没写完。
传球过程形成基环内向森林（一个点的自环也算环）。

1. 对于环上的点，答案是若干个整环求和，加首尾零散的部分，可以用前缀和求区间和。
2. 对于不在环上的点，维护一个栈，保存到环过程中的权值。维护一个值，保存当前点到环（至多含k个值）的权值和。不足k时，加上环上部分，可能是一段，或若干个整环加首尾零散的部分。

O(n)

class Solution {
public:long long getMaxFunctionValue(vector<int>& receiver, long long k) {}
};