Diffusion

news/2025/1/8 3:34:11/文章来源:https://www.cnblogs.com/GraphL/p/18656622

所以我可以理解成这里其实是计算一条轨迹每个点都要用来预测噪声？

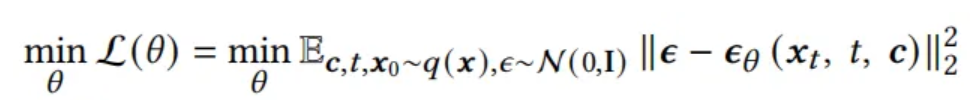
是的，你的理解是正确的。

在这个公式中：
$ \min_\theta \mathcal{L}(\theta) = \min_\theta \mathbb{E}_{c,t,x_0 \sim q(x), \epsilon \sim \mathcal{N}(0, I)} \| \epsilon - \epsilon_\theta (x_t, t, c) \|_2^2 $

解析：

$ x_0 $ 表示真实轨迹，每个轨迹由多个轨迹点组成。
$ x_t $ 是在时间步 $ t $ 添加噪声后的轨迹。
$ \epsilon \sim \mathcal{N}(0, I) $ 是一个从标准正态分布中采样的噪声，与轨迹的形状相同。
$ \epsilon_\theta (x_t, t, c) $ 是模型在带噪轨迹 $ x_t $、时间步 $ t $ 和条件 $ c $ 下预测的噪声。

逐点预测噪声：

轨迹 $ x_t $ 通常表示为 $ L \times 2 $ 的矩阵，$ L $ 是轨迹点的数量，每个点有两个坐标（经度和纬度）。
损失函数计算的是模型预测的噪声 $ \epsilon_\theta $ 与真实噪声 $ \epsilon $ 之间的欧几里得距离。
由于轨迹由多个点组成，模型实际上是针对轨迹中每个点的噪声进行预测和优化的。

直观理解：

轨迹中的每个点都会有一个对应的噪声值。
模型在训练过程中，需要学习如何去预测整个轨迹在任意时间步的噪声，从而在去噪过程中逐点恢复轨迹。
最终损失是所有轨迹点噪声预测误差的总和。

如果你希望进一步探讨扩散模型的噪声预测机制或轨迹生成细节，可以继续交流！

so how this paper evalute this model?

论文通过多种方式对模型进行评估。以下是主要评估方法的总结：

1. 定量指标：

论文使用三个主要指标与基线方法进行比较：

密度误差 (Density Error)：衡量生成轨迹与真实地理分布的匹配程度。

# 将城市划分为16x16的网格
# 比较真实数据和生成数据的点分布
Density_Error = JSD(real_distribution, generated_distribution)

行程误差 (Trip Error)：评估生成轨迹的起点和终点是否真实可信。

# 比较起点/终点分布
Trip_Error = JSD(real_trip_patterns, generated_trip_patterns)

长度误差 (Length Error)：检查轨迹距离是否符合实际情况。

# 比较距离分布
Length_Error = JSD(real_distances, generated_distances)

2. 实用性评估：

测试生成数据是否对下游任务有帮助：

# 以交通流量预测作为测试案例
for model in [ASTGCN, GWNet, MTGNN, DCRNN]:# 比较使用真实数据和生成数据的性能real_performance = train_and_evaluate(model, real_data)gen_performance = train_and_evaluate(model, generated_data)compare_metrics(real_performance, gen_performance)

3. 轨迹控制能力测试：

评估生成轨迹是否遵循给定约束条件：

生成路径与规划路线的可视化比较。
测试轨迹是否遵循道路网络拓扑结构。

4. 泛化能力测试：

测试模型的零样本学习 (Zero-shot learning) 能力：

# 在一个城市训练，在另一个城市测试，无需重新训练
model.train(chengdu_data)
generated = model.generate(xian_road_network)
evaluate_quality(generated, xian_real_data)

结果对比：

论文显示，ControlTraj 在以下基线方法中表现优于：

VAE [45]
TrajGAN [44]
DP-TrajGAN [51]
Diffwave [20]
DiffTraj [55]

在所有这些指标上，ControlTraj 提供了更好的控制能力和泛化能力。

需要我进一步解释这些评估方法的任何部分吗？

将道路拓扑和行程属性作为条件信息。所以这个模型主要想解决的就是这个问题，从很少的信息出发，恢复完整的轨迹。简短回答即可

是的，这个模型的核心目标是利用道路拓扑和行程属性作为条件，从有限或少量信息出发，生成或恢复完整的轨迹。

实际的应用场景

你提出的关于训练过程与实际应用场景之间关系的观点非常重要。让我来详细解析一下：

训练过程：

使用真实轨迹数据。
逐步添加噪声（正向过程）。
学习去除噪声（反向过程）。
将道路拓扑和行程属性作为条件信息。

实际应用场景：

1. 隐私保护数据共享

# 不直接分享真实用户轨迹，而是生成合成轨迹
synthetic_trajectories = generate_trajectories(road_network=city_roads,trip_attributes={"departure_time": "8:00 AM","travel_distance": "5km","average_speed": "30km/h"}
)

通过生成与实际轨迹相似的合成轨迹，保护用户隐私，避免暴露真实行程路径。

2. 数据增强

# 当真实轨迹数据有限时
augmented_data = generate_similar_trajectories(road_constraints=existing_routes,desired_count=1000
)

生成额外的合成轨迹数据，扩充数据集，提高模型训练的鲁棒性和泛化能力。

3. 路线规划

# 在给定约束条件下生成可能的行车路线
possible_routes = generate_trajectories(start_point=(lat1, lng1),end_point=(lat2, lng2),road_network=available_roads,time_of_day="rush_hour"
)

通过输入起点和终点，结合实时道路网络和时间条件，生成最优或多种可能路线，为导航系统提供参考。

4. 仿真与测试

# 生成逼真的交通流量模式
simulated_traffic = generate_trajectories(road_network=test_area,time_period="full_day",traffic_conditions="heavy"
)

在特定区域和时间段内模拟不同的交通状况，为交通流量预测和城市规划提供数据支持。

关键点总结：

训练过程通过在真实轨迹上添加和去除噪声来学习轨迹生成的潜在模式。
实际应用从纯噪声开始，利用模型学习到的模式生成新的轨迹。
生成的轨迹遵循道路拓扑和行程属性约束，可以创造全新的、逼真的路径。

因此，在训练中使用的加噪和去噪过程，只是一种学习轨迹生成模式的机制。而在实际应用中，模型根据给定条件和约束生成完全新的轨迹，从而满足隐私保护、数据增强、路线规划和仿真等多种需求。

我想知道你逐步去噪的时候，这个值是一个初始加噪的值，是一个值还是一个向量？

在扩散模型中，损失函数：

$ L(\theta) = \mathbb{E}_{t, x_0, \epsilon} \left[ \| \epsilon - \epsilon_\theta(x_t, t, c) \|^2 \right] $

中，$ \epsilon $ 是一个向量，而不是单一的标量值。

1. 为什么 $ \epsilon $ 是向量？

在轨迹生成任务中，$ x_0 $ 是一个轨迹，由多个轨迹点（例如 GPS 坐标）组成，每个轨迹点通常包含两个维度（经度和纬度）。
噪声 $ \epsilon $ 会与轨迹点逐个对应，因此 $ \epsilon $ 和 $ x_t $ 都是与轨迹形状相同的向量或矩阵。
例如，如果轨迹 $ x_0 $ 由 $ L $ 个点组成，每个点有两个坐标（纬度和经度），那么：
$ x_0 \in \mathbb{R}^{L \times 2} $
同样，噪声 $ \epsilon $ 也服从相同的形状：
$ \epsilon \in \mathbb{R}^{L \times 2} $

2. 损失函数中的噪声表示：

模型 $ \epsilon_\theta(x_t, t, c) $ 输出的是一个与噪声 $ \epsilon $ 相同形状的向量或矩阵，表示模型预测的噪声。
损失函数计算的是预测噪声和真实加噪的噪声之间的逐元素差异（通过欧几里得距离的平方表示）：
$ \| \epsilon - \epsilon_\theta(x_t, t, c) \|^2 = \sum_{i=1}^{L} \sum_{j=1}^{2} (\epsilon_{ij} - \epsilon_{\theta, ij})^2 $
这里 $ i $ 表示轨迹点的索引，$ j $ 表示纬度或经度维度。

3. 直观理解：

向量形式：
噪声 $ \epsilon $ 可能看起来像这样：
$ \epsilon = \begin{pmatrix} 0.1 & -0.3 \\ -0.2 & 0.4 \\ 0.05 & -0.1 \end{pmatrix} $
每个元素代表轨迹中每个点在不同维度上的噪声扰动。
标量形式（错误理解）：
如果 $ \epsilon $ 是标量，那它只能表示对整个轨迹的统一扰动，这样模型将无法学到轨迹中每个点的细粒度差异。因此，使用向量是必须的。

4. 逐步去噪时 $ \epsilon $ 的变化：

在去噪过程中，每次迭代都会预测整个轨迹中每个轨迹点的噪声，因此：
$ \epsilon_\theta(x_t, t, c) \in \mathbb{R}^{L \times 2} $
模型通过逐步减少噪声，最终将轨迹从纯噪声 $ x_T $ 逐步恢复到真实轨迹 $ x_0 $。

5. 总结：

噪声 $ \epsilon $ 是一个与轨迹相同形状的向量或矩阵，而非单一的标量值。
每个轨迹点都添加独立的噪声，使得扩散模型能更精细地学习轨迹生成任务。
损失函数衡量的是模型在整个轨迹空间内对噪声的逐点预测误差，确保模型能逐步去除不同程度的噪声。

如果你还有其他关于扩散模型或轨迹生成的细节问题，欢迎继续讨论！

所以我想知道，它这里的噪声是逐步添加的，还是直接可以算出来第T步的噪声然后添加的？

在扩散模型中，噪声的添加方式可以理解为一步计算直接得到第 $ t $ 步的加噪结果，而不是逐步累积地逐步添加噪声。

1. 噪声添加方式解析：

当计算第 $ t $ 步的带噪轨迹 $ x_t $ 时，可以直接通过以下公式一次性生成：
$ x_t = \sqrt{\bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon $
其中：

$ x_0 $ 是原始轨迹数据（无噪声）。
$ \epsilon \sim N(0, I) $ 是从标准正态分布中采样的随机噪声。
$ \bar{\alpha}_t $ 是一个由时间步 $ t $ 决定的衰减系数（或称为加权因子），表示轨迹在扩散过程中保留多少原始信号。

2. 逐步添加 vs 直接计算

直接计算方式（扩散过程实际使用的方式）：
- 公式可以直接在任意时间步 $ t $ 计算轨迹加噪后的状态 $ x_t $。
- 不需要逐步迭代地添加噪声，可以通过简单的计算直接得到第 $ t $ 步结果。
- 例如，如果想计算 $ T $ 步的加噪轨迹，只需要带入 $ t = T $ 即可：
  $ x_T = \sqrt{\bar{\alpha}_T} x_0 + \sqrt{1 - \bar{\alpha}_T} \epsilon $
  这个计算在一步内完成，不需要从 $ t = 0 $ 逐步加到 $ T $。
逐步添加方式（理论上可以迭代实现，但效率较低）：
- 在某些理论描述中，可以将扩散过程理解为逐步添加噪声的过程，即从 $ x_0 \to x_1 \to x_2 \to ... \to x_T $。
- 每一步添加少量噪声：
  $ x_{t+1} = \sqrt{\alpha_t} x_t + \sqrt{1 - \alpha_t} \epsilon_t $
- 这种方式实际上较少直接应用于模型中，因为直接计算更简单且高效。

3. 直观理解：

逐步添加的方式像是一步步“盖住轨迹”的过程，每次盖上一点噪声，逐渐模糊轨迹。
直接计算方式就像是直接“涂抹”一个计算好的噪声层，立刻得到最终的加噪轨迹。

扩散模型通常使用直接计算方式，因为它更简洁高效，不需要逐步迭代，减少了计算复杂度。

4. 总结：

噪声添加是直接计算的，而不是逐步累积的。
你可以直接计算出任意时间步 $ t $ 的加噪轨迹，而无需依次迭代所有时间步。
这种直接计算方式让扩散模型在训练和生成阶段都能快速地对轨迹进行加噪或去噪处理。

如果对扩散过程或逆向去噪过程有更多疑问，可以继续深入探讨！

随机选择时间步 t 。这里是加t个时间步的噪声？另外，它输入的是轨迹还是embedding，初始轨迹怎么加噪呀

1. 关于“随机选择时间步 $ t $”的理解：

在扩散模型中，随机选择时间步 $ t $ 代表在扩散过程中对轨迹 $ x_0 $ 添加 $ t $ 步噪声。

当 $ t = 0 $ 时，表示原始轨迹 $ x_0 $ 无噪声。
当 $ t = T $ 时，表示轨迹完全被噪声覆盖，接近纯高斯噪声。

具体含义：

扩散过程逐步将轨迹 $ x_0 $ 转化为噪声，通过逐步添加不同程度的噪声，使其在 $ t $ 步之后变成 $ x_t $。
逆过程通过逐步去噪，从 $ x_T $ 恢复到 $ x_0 $，生成接近真实轨迹的数据。

公式表示为：
$ x_t = \sqrt{\bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon $
其中：

$ \bar{\alpha}_t $ 是扩散过程中的衰减系数（定义模型如何平滑地添加噪声）。
$ \epsilon \sim N(0, I) $ 是加到轨迹上的随机噪声。

2. 输入的是轨迹还是嵌入？

输入数据：

输入的是轨迹本身，而不是直接输入嵌入。
轨迹数据 $ x_0 $ 通常表示为一系列GPS点的序列（例如：经纬度坐标序列）。

轨迹如何参与扩散？

轨迹 $ x_0 $ 直接参与加噪，扩散过程操作的是轨迹点的坐标数据。
轨迹点 $ x_0 = [x_0^1, x_0^2, ..., x_0^L] $，其中 $ L $ 是轨迹点的数量，每个点 $ x_0^i $ 包含经纬度或坐标信息。

具体过程：

加噪前：轨迹数据是一个 $ L \times 2 $ 维矩阵，表示 $ L $ 个GPS坐标点（每个点有两个坐标：纬度和经度）。
$ x_0 = \begin{pmatrix} 30.1 & 30.3 & 30.5 & 30.7 & 30.9 \\ 114.2 & 114.4 & 114.6 & 114.8 & 115.0 \end{pmatrix} $
加噪过程：对轨迹的每个点坐标添加噪声，使得轨迹逐渐偏离真实路径。

3. 初始轨迹如何加噪？

加噪的具体方式：
$ x_t = \sqrt{\bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon $

解读：

$ x_0 $ 是原始轨迹，表示为坐标点的序列。
$ x_t $ 是在时间步 $ t $ 加噪后的轨迹。
$ \epsilon $ 是加到轨迹上的随机噪声矩阵，形状与 $ x_0 $ 相同，每个坐标点独立加噪。

例子：

假设原始轨迹 $ x_0 $ 为：
$ x_0 = \begin{pmatrix} 30.0 & 30.2 & 30.4 \\ 114.0 & 114.3 & 114.5 \end{pmatrix} $
加噪后：
$ x_t = \sqrt{\bar{\alpha}_t} \cdot \begin{pmatrix} 30.0 & 30.2 & 30.4 \\ 114.0 & 114.3 & 114.5 \end{pmatrix} + \sqrt{1 - \bar{\alpha}_t} \cdot \begin{pmatrix} 0.1 & -0.3 & 0.4 \\ 0.2 & -0.1 & 0.3 \end{pmatrix} $
噪声扰动轨迹坐标，使其逐渐接近纯噪声分布。

4. 嵌入何时出现？

嵌入（embedding）通常出现在条件信息部分，而非直接对轨迹加噪。
在扩散模型中，轨迹数据本身参与加噪，而条件信息（如道路嵌入和行程属性）作为额外引导，通过交叉注意力（cross-attention）影响去噪过程。

流程示意：

轨迹 $ x_0 $ 直接加噪得到 $ x_t $。
GeoUNet 使用带噪轨迹 $ x_t $ 和条件信息 $ c $（包括道路嵌入和行程属性嵌入）进行去噪，预测轨迹中的噪声 $ \epsilon $。
嵌入只参与条件控制，不直接加噪。

5. 总结

加噪的输入是轨迹坐标本身，而非嵌入。
嵌入是条件信息，用于辅助去噪过程，但不直接参与加噪轨迹数据。
初始轨迹加噪的方式是通过逐步添加随机噪声，使轨迹逐渐偏离真实路径，最终在逆扩散过程中通过条件信息恢复成真实轨迹。

如果你对嵌入部分或加噪机制还有进一步的疑问，可以继续深入探讨！

帮我解读一下这里的过程，最后用公式表示

解读扩散训练和生成过程：

1. 扩散训练过程解析：

目标：训练GeoUNet模型，使其能够准确预测轨迹数据中的噪声，最终通过逆扩散过程生成高保真轨迹。

步骤解析：

真实轨迹初始化：
$ x_0 = \text{real\_trajectory} $
轨迹数据 $ x_0 $ 是原始无噪声的真实轨迹。
**随机选择时间步 $ t $**： $
t \sim \text{Uniform}({1, ..., T})
$
在扩散过程中，随机选择一个时间步 $ t $ 进行训练，确保模型能在不同时间步下都能有效去噪。
生成随机噪声：
$ \epsilon \sim N(0, I) $
从标准正态分布中采样噪声 $ \epsilon $，该噪声将用于轨迹数据的扰动。
添加噪声到轨迹：
$ x_t = \sqrt{\bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon $
使用预定义的扩散系数 $ \bar{\alpha}_t $ 生成带噪轨迹 $ x_t $。
该公式来自扩散模型的前向过程，将真实轨迹 $ x_0 $ 加噪生成 $ x_t $。
GeoUNet预测噪声：
$ \epsilon_\theta(x_t, t, c) $
使用GeoUNet模型预测在时间步 $ t $ 下的噪声，其中 $ c $ 表示条件信息（包括道路嵌入和行程属性）。
计算损失（均方误差，MSE）：
$ L(\theta) = \mathbb{E}_{t, x_0, \epsilon} \left[ \| \epsilon - \epsilon_\theta(x_t, t, c) \|^2 \right] $
训练目标是最小化模型预测噪声和真实噪声之间的均方误差，优化模型参数 $ \theta $。

2. 轨迹生成过程解析：

目标：通过逆扩散过程逐步去除噪声，从纯噪声中生成符合道路约束和行程属性的轨迹。

步骤解析：

获取条件信息：
$ c = \text{get\_conditions(road\_segments, attributes)} $
从道路段和行程属性中获取条件信息 $ c $，确保生成的轨迹遵循地理和行程约束。
从纯噪声开始生成：
$ x_T \sim N(0, I) $
初始轨迹 $ x_T $ 为标准正态分布中的随机噪声。
逆扩散过程（逐步去噪）：
对 $ t = T, T-1, ..., 1 $ 进行迭代，逐步去噪直到生成最终轨迹。

在每个时间步 $ t $：
1. 预测当前时间步下的噪声：
  $ \epsilon_\theta(x_t, t, c) $
2. 计算去噪轨迹 $ x_{t-1} $： $
  x_{t-1} = \frac{1}{\sqrt{\alpha_t}} \left(x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}t}} \epsilon\theta(x_t, t, c) \right) + \sigma_t z
  $ 其中，$ \alpha_t $ 是扩散系数，$ \sigma_t $ 是去噪过程中的方差调整，$ z \sim N(0, I) $ 是随机噪声。
返回最终生成轨迹：
$ x_0 $
当 $ t = 0 $ 时，得到最终生成的轨迹 $ x_0 $。

公式总结：

训练阶段：

噪声添加（前向过程）：
$ x_t = \sqrt{\bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon $
噪声预测（GeoUNet）：
$ \epsilon_\theta(x_t, t, c) $
损失函数：
$ L(\theta) = \mathbb{E}_{t, x_0, \epsilon} \left[ \| \epsilon - \epsilon_\theta(x_t, t, c) \|^2 \right] $

生成阶段（逆向过程）：

初始化：
$ x_T \sim N(0, I) $
逐步去噪：
$ x_{t-1} = \frac{1}{\sqrt{\alpha_t}} \left(x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_\theta(x_t, t, c) \right) + \sigma_t z $
最终轨迹输出：
$ x_0 $

这个过程确保生成轨迹不仅具有真实感，还能符合道路网络和行程条件，从而实现高精度和可控的轨迹生成。

条件信息 (𝒄)

3.2 GeoUNet架构：

输入：

带噪轨迹 (𝒙˜t)：
- 通过在原始轨迹上添加噪声生成。
- 表示扩散过程在时间步 $ t $ 时的轨迹状态。
条件信息 (𝒄)：
- 道路嵌入 (𝒛L)： 来自预训练的RoadMAE模型。
- 行程属性 (𝒛attr)：
  - 出发时间
  - 行程时间
  - 总行程距离
  - 平均速度
  - 轨迹点数量

过程：

GeoUNet 预测噪声水平 $ ϵθ(𝒙˜t, t, 𝒄) $。
使用地理注意力机制融合条件信息。
通过下采样/上采样块处理轨迹特征。

3.3 轨迹生成控制：

主要包括两个过程：

训练过程：

# 输入：
- 道路段 r
- 掩码比例 ro
- 轨迹属性# 步骤：
1. 通过RoadMAE编码器获取掩码嵌入 zL
2. 获取条件引导 c = Concat(zattr, zL)
3. 从轨迹分布 q(x) 采样 x0
4. 从均匀分布 Uniform({1,...,T}) 采样 t，ϵ ~ N(0,I)
5. xt = x0 + √(1-α̅t)ϵ
6. 更新梯度：∇θ||ϵ - ϵθ(xt, t, c)||²

生成过程：

# 输入：
- 道路段 r
- 轨迹属性# 步骤：
1. 获取道路段嵌入 zL
2. 获取条件引导 c = Concat(zattr, zL)
3. 从标准正态分布 N(0,I) 采样 x̃T
4. 对于 t = T, T-1, ..., 1：- 计算 μθ(x̃t, t, c)- 计算 pθ(x̃t-1|x̃t, c)
5. 返回 x̃0（最终生成的轨迹）