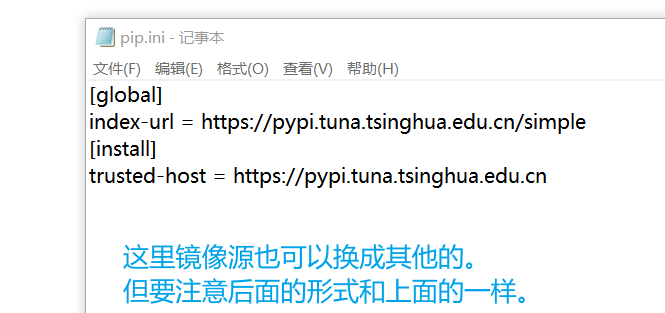
题目描述
给定 \(n\) 个点的树和 \(m\) 条路线,每条路线连接路径 \((u,v)\) 之间的所有点。
\(q\) 次询问,从 \(u\) 到 \(v\) 至少要经过多少条路线。
数据范围
- \(2\le n\le 2\cdot 10^5,1\le m\le 2\cdot 10^5,1\le q\le 2\cdot 10^5\) 。
时间限制 \(\texttt{3s}\) ,空间限制 \(\texttt{256MB}\) 。
分析
容易想到的贪心策略是每一步跳到可到达的深度最小的点。
用倍增加速上述过程,预处理 \(f_{u,i}\) 表示从 \(u\) 出发跳 \(2^i\) 步能到达的最浅点。
什么时候贪心会出问题?记 \(p=lca(u,v)\) ,只要跳完以后仍在子树内就无脑跳(一定最优),如果从 \(x,y\) 再跳一步就要到 \(p\) 及其祖先,但是 \(x,y\) 在同一条路线上,那么只需要一条路径(原策略需要两条)。
注意如果 \((u,v)\) 是一条直上直下的链就不需要考虑这种情况。
于是问题转化为如何判断 \((x,y)\) 是否在同一条路径上,这等价于判断是否存在路线 \((u,v)\) 满足 \(u\) 在 \(x\) 子树内, \(v\) 在 \(y\) 子树内。
将 \((u,v)\) 看成二维平面上的点 \((dfn_u,dfn_v),(dfn_v,dfn_u)\) ,只需判断横坐标 \([dfn_x,dfn_x+sz_x-1]\) ,纵坐标 \([dfn_y,dfn_y+sz_y-1]\) 的矩形框中是否有点。
这是经典二维数点问题,离线扫描线 \(+\) 树状数组解决。
时间复杂度 \(\mathcal O((n+m+q)\log n)\) 。
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+5;
int m,n,p,q,u,v,cnt;
int d[maxn],fa[maxn],sz[maxn],son[maxn];
int dfn[maxn],top[maxn];
int f[maxn][18];
int c[maxn],res[maxn],val[maxn];
vector<int> g[maxn],h[maxn];
struct oper
{int l,r,op,id;
};
vector<oper> vec[maxn];
void dfs1(int u)
{sz[u]=1;for(auto v:g[u]){d[v]=d[u]+1,fa[v]=u,dfs1(v),sz[u]+=sz[v];if(sz[v]>sz[son[u]]) son[u]=v;}
}
void dfs2(int u,int f)
{dfn[u]=++cnt,top[u]=f;if(son[u]) dfs2(son[u],f);for(auto v:g[u]) if(v!=son[u]) dfs2(v,v);
}
int lca(int u,int v)
{while(top[u]!=top[v]) d[top[u]]>d[top[v]]?u=fa[top[u]]:v=fa[top[v]];return d[u]<d[v]?u:v;
}
void add(int x,int v)
{while(x<=n) c[x]+=v,x+=x&-x;
}
int query(int x)
{int res=0;while(x) res+=c[x],x-=x&-x;return res;
}
int main()
{scanf("%d",&n);for(int i=2;i<=n;i++) scanf("%d",&u),g[u].push_back(i);d[1]=1,dfs1(1),dfs2(1,1);for(int i=1;i<=n;i++) f[i][0]=i;scanf("%d",&m);while(m--){scanf("%d%d",&u,&v),p=lca(u,v);f[u][0]=min(f[u][0],p),f[v][0]=min(f[v][0],p);h[dfn[u]].push_back(dfn[v]),h[dfn[v]].push_back(dfn[u]);}for(int u=n;u>=1;u--) for(auto v:g[u]) f[u][0]=min(f[u][0],f[v][0]);for(int i=1;i<18;i++) for(int u=1;u<=n;u++) f[u][i]=f[f[u][i-1]][i-1];scanf("%d",&q);for(int i=1;i<=q;i++){scanf("%d%d",&u,&v),p=lca(u,v);for(int j=17;j>=0;j--){if(f[u][j]>p) u=f[u][j],res[i]+=1<<j;if(f[v][j]>p) v=f[v][j],res[i]+=1<<j;}if(f[u][0]>p||f[v][0]>p) res[i]=-1;else{if(u==p||v==p) res[i]++;else{vec[dfn[u]-1].push_back({dfn[v],dfn[v]+sz[v]-1,-1,i});vec[dfn[u]+sz[u]-1].push_back({dfn[v],dfn[v]+sz[v]-1,1,i});}}}for(int i=1;i<=n;i++){for(auto p:h[i]) add(p,1);for(auto [l,r,op,id]:vec[i]){val[id]+=(query(r)-query(l-1))*op;if(op==1) res[id]+=val[id]?1:2;}}for(int i=1;i<=q;i++) printf("%d\n",res[i]);return 0;
}