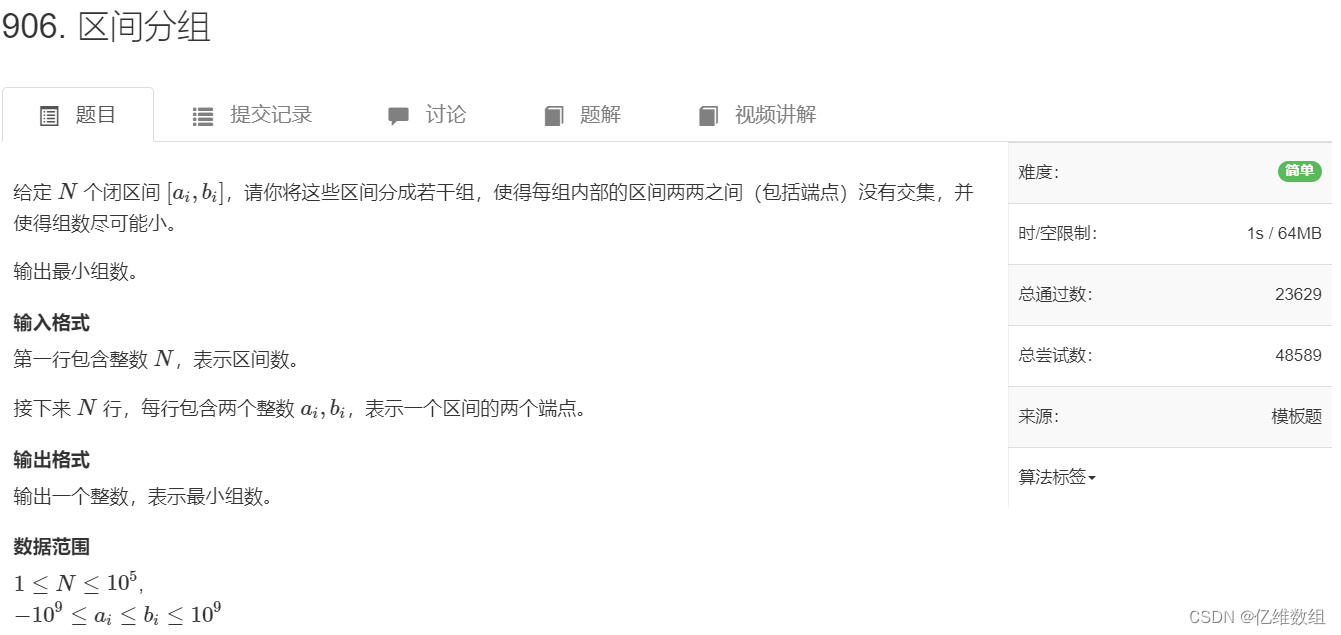
题目描述

 

贪心策略 

先按照左端点对所有区间进行排序，然后从左到右遍历每一个区间，如果遍历到的区间能够加入现在已经存在的某一个区间组中，则加入，否则，创建新的区间组，并将这个区间加入。

具体的方案是用小根堆存储每一个区间组的区间中最大的右端点值（想一想为什么用小根堆存储？）然后比较遍历到的区间左端点l和从小根堆堆顶中取到的这个右端点值r：

若l<=r则不能加入任何区间组

若l>r可以加入含有最大右端点值为r的区间组当中，更新这个最大右端点值（方法是：从大根堆中取出堆顶并把新的区间的右端点入堆）

贪心策略证明

这一题的证明与acwing905有异曲同工之妙，这里就不那么详细了，思想也可以参照那道题目的题解：

acwing905贪心策略清晰证明

同样的设：

ans为所有分组方案的最小分组数

cnt为根据上述贪心策略得到的最小分组数

现在的目标是证明：ans>=cnt&&ans<=cnt

对于ans<=cnt是根据假设得到的显而易见的结论

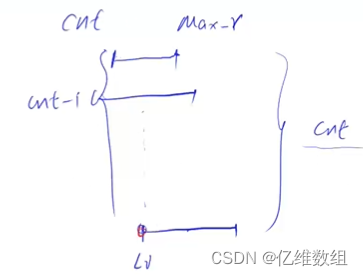
对于cnt>=ans，假设下图这种情况，将要产生第cnt个分组了，那么前cnt-1个区间组的最后一个区间一定和这个新区间有着公共点Li，与其它区间相交了cnt次，既然对于所有的区间存在这么一个相交cnt次的公共点li，那么在分组的时候，至少就必须有cnt组，至于是不是比如大于我们不用管，有了前面的这个“至少”就已经完全可以说明所有方案的分组数全部>=cnt,那么最小的分组数就必然大于等于cnt，证毕。

 代码

#include<iostream>
#include<queue>
#include<algorithm>
#include<map>
using namespace std;
typedef pair<int,int>PII;
const int N=100010;
int n;
PII range[N];
int main()
{scanf("%d",&n);for(int i=0;i<n;i++)scanf("%d%d",&range[i].first,&range[i].second);priority_queue<int,vector<int>,greater<int>>heap;sort(range,range+n);for(int i=0;i<n;i++){if(heap.empty()||heap.top()>=range[i].first)heap.push(range[i].second);else{heap.pop();heap.push(range[i].second);}}cout<<heap.size();return 0;
}